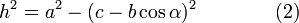Видео:№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать

Признаки параллельных прямых
1. Если две прямые параллельны третьей прямой, то они являются параллельными:
2. Если две прямые перпендикулярны третьей прямой, то они параллельны:
Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.
3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:
Если ∠1 + ∠2 = 180°, то a || b.
4. Если соответственные углы равны, то прямые параллельны:
5. Если внутренние накрест лежащие углы равны, то прямые параллельны:
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Свойства параллельных прямых
Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.
1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:
Если a || b, то ∠1 + ∠2 = 180°.
2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:
3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:
Следующее свойство является частным случаем для каждого предыдущего:
4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:
Пятое свойство — это аксиома параллельности прямых:
5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Доказательство теоремы о свойстве односторонних углов при пересечении двух параллельных прямых третьей прямой.
Видео:Углы при пересечении двух прямых третьейСкачать

Ваш ответ
Видео:Углы, образованные при пересечении двух прямых секущейСкачать

решение вопроса
Видео:УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,680
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Углы при пересечении двух прямых секущей (третьей прямой). Виды углов урок 5. Геометрия 7 класс.Скачать

ГЕОМЕТРИЯ 9 класс
Билет № 1
1. Углы, образованные при пересечении двух параллельных прямых третьей прямой. Свойство внутренних односторонних углов.
2. Треугольник: определение и виды. Теорема косинусов (доказательство). Следствия из теоремы косинусов.
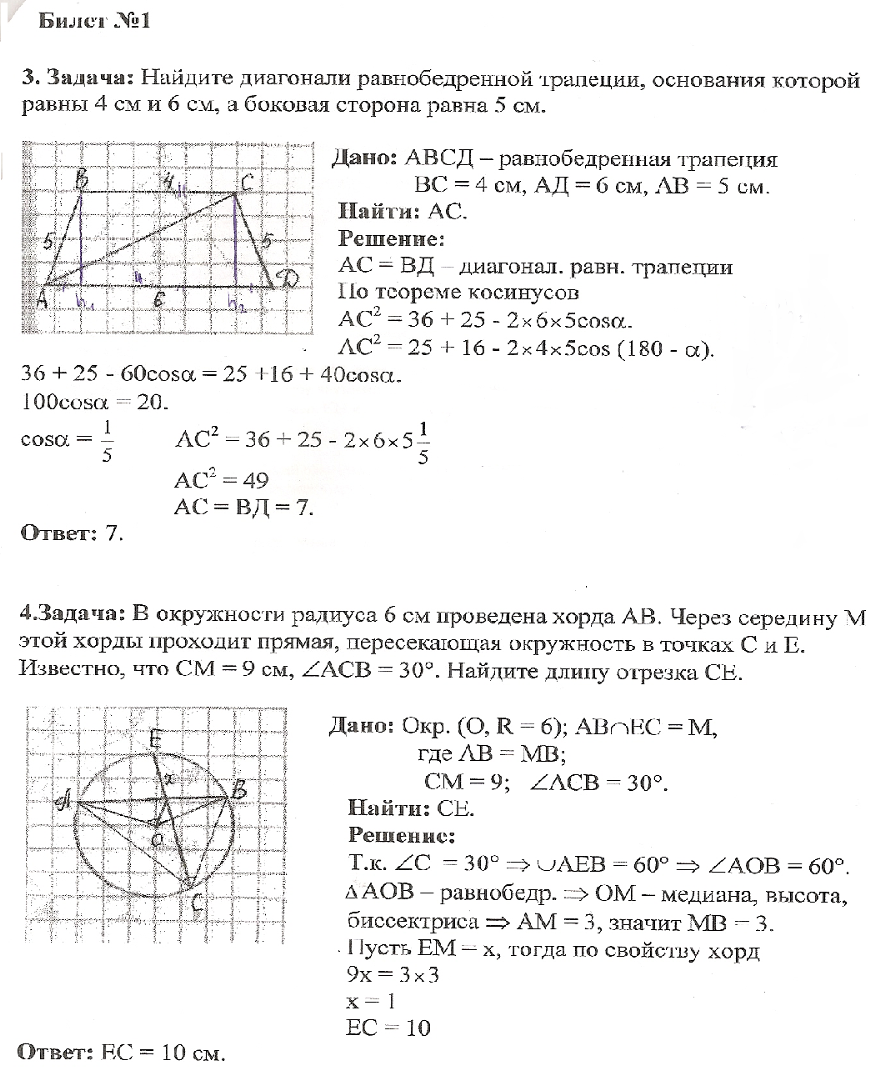
3. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.
4. В окружности радиуса 6 см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ = 9 см, —>
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Главная
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Билет 1
- >» src=»http://narod2.yandex.ru/i/users/color/red/arrow-s3.png» />Билет 2
1) Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.
 Свойство внутренних односторонних углов:
Свойство внутренних односторонних углов:
Если при пересечении двух прямых, лежащих в одной плоскости, третьей прямой углы одной из пар соответственных или накрест лежащих углов равны, то сумма углов каждой пары односторонних углов равна 180 градусов.
2) Треуго́льник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки
| Типы треугольников | ||
|---|---|---|
 Остроугольный |  Тупоугольный |  Прямоугольный |
 Разносторонний |  Равнобедренный | 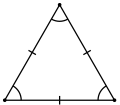 Равносторонний |
По величине углов
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми(меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
По числу равных сторон
- Разносторонним называется треугольник, у которого длины трёх сторон различны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называютсябоковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора:
Для плоского треугольника со сторонами a,b,c и углом α , противолежащим стороне a , справедливо соотношение: 
Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
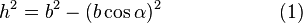
Приравниваем правые части уравнений (1) и (2) и:
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Выражения для сторон b и c:
3)
🌟 Видео
№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ 4. Углы, образованные при пересечении двух параллельных прямых третьейСкачать

7 класс. Геометрия. Параллельность прямых. Признаки и свойства. Углы при пересечении прямых. Урок #7Скачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Углы при пересечении двух прямых секущей. Свойства и признаки параллельности прямых.Скачать

ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Углы, получаемые при сечении двух прямых третьей.Скачать

УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать






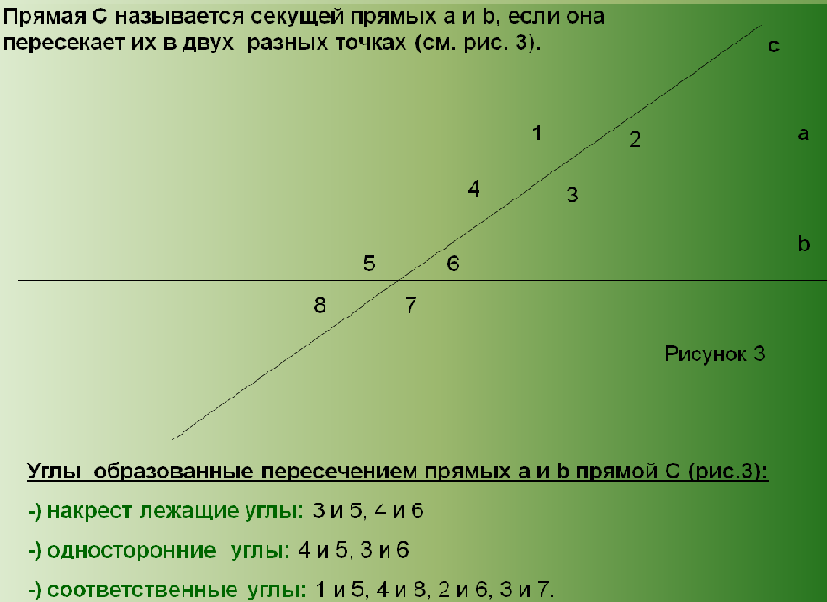 Свойство внутренних односторонних углов:
Свойство внутренних односторонних углов: