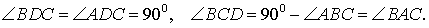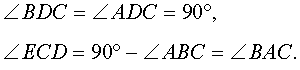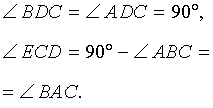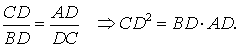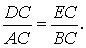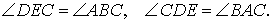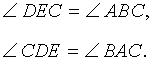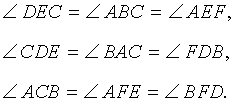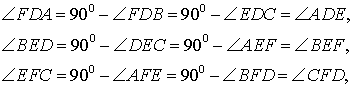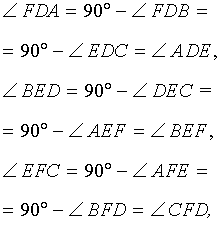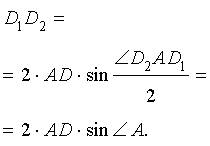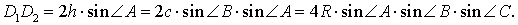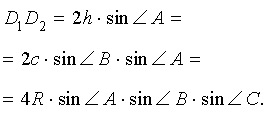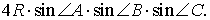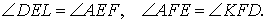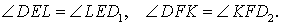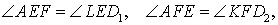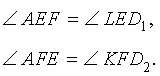В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.
- Определение высоты треугольника
- Высота в разных видах треугольников
- Свойства высоты треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Высота треугольника. Задача Фаньяно
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
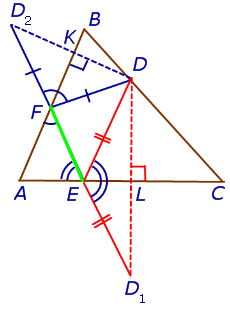
- Задача Фаньяно
- Теорема о пересечении высот треугольника
- 🔍 Видео
Видео:Геометрия 8 класс (Урок№31 - Теорема о пересечении высот треугольника.)Скачать

Определение высоты треугольника
Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.
Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).
Обычно высота обозначается буквой h (иногда как ha – это означает, что она проведена к стороне a).
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота в разных видах треугольников
В зависимости от вида фигуры высота может:
- проходить внутри треугольника (в остроугольном △);
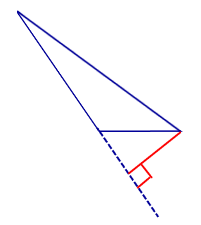
- проходить за рамками треугольника (в тупоугольном △);
- являться одним из катетов (в прямоугольном △), за исключением высоты, проведенной к гипотенузе.
Видео:8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Свойства высоты треугольника
Свойство 1
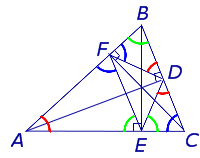
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).
- в остроугольном треугольнике;
- в тупоугольном треугольнике;
- в прямоугольном треугольнике.
Вершина A является, в т.ч., точкой пересечения высот.
Свойство 2
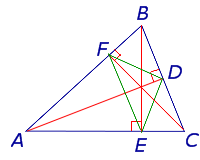
При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:
- △ABE∼△CBF: по двум углам (∠ABC – общий, ∠AEB и ∠CFB являются прямыми).
- △AFG∼△CEG: по двум углам (∠AFG и ∠CEG – прямые, ∠AGF и ∠CGE равны как вертикальные углы).
- △ABC∼△BEF: по трем равным углам (∠ABC = ∠EBF, ∠ACB = ∠BFE, ∠CAB = ∠BEF).
Примечание: доказательство подобия последней пары треугольников достаточно длинное и не является целью данной статьи, поэтому подробно останавливаться на нем будем.
Свойство 3
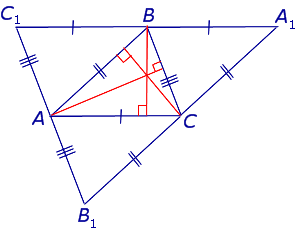
Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.
Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.
Свойство 4
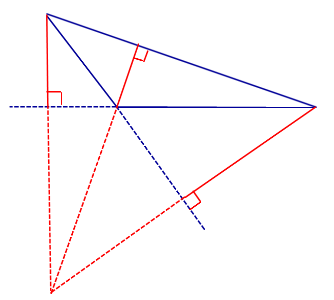
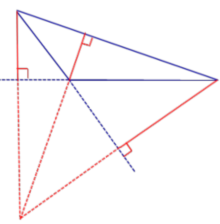
Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.
Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.
Видео:Свойство биссектрисы треугольника с доказательствомСкачать

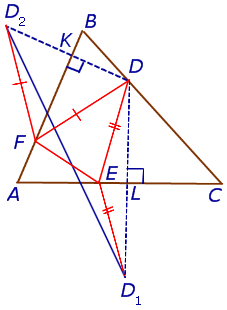
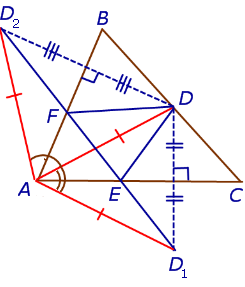
Высота треугольника. Задача Фаньяно
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:ПЕРЕСЕЧЕНИЕ ВЫСОТ треугольника ТЕОРЕМА 8 класс АтанасянСкачать

Высота треугольника. Свойство высоты прямоугольного треугольника
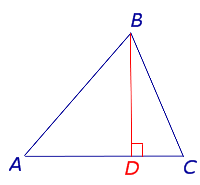
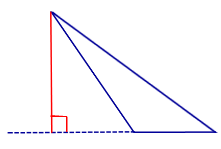
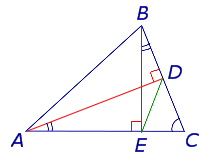
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
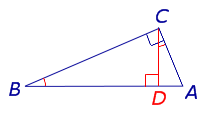
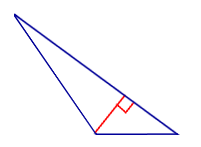
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:Теорема о пересечении высот треугольника | Геометрия 7-9 класс #73 | ИнфоурокСкачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 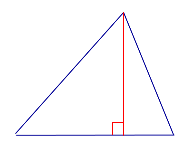 | Все высоты остроугольного треугольника лежат внутри треугольника. |
 | ||
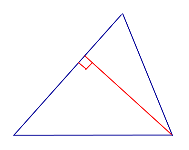 | ||
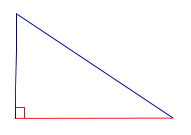
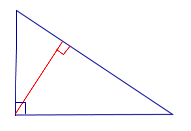
| Прямоугольный треугольник | 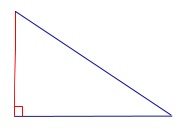 | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
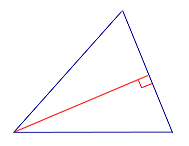
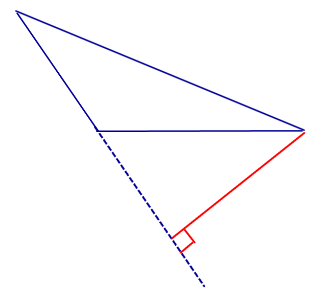
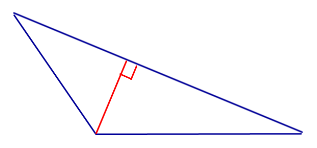
| Тупоугольный треугольник | 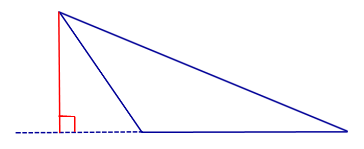 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
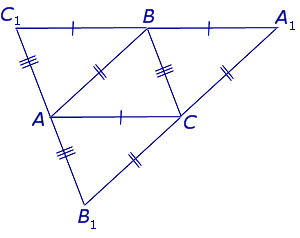
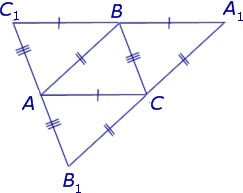
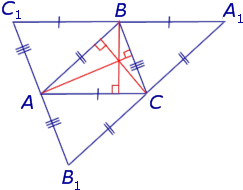
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 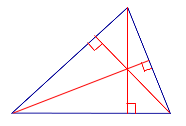 | |
| Прямоугольный треугольник | 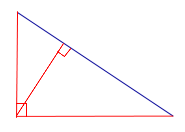 |