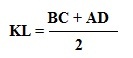Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
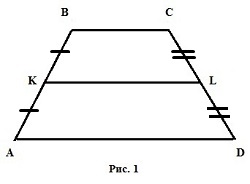
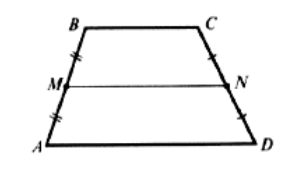
Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).
- Свойства средней линии трапеции
- Доказательство теоремы о средней линии трапеции
- Научная работа по теме «Средняя линия трапеции (несколько способов доказательств)», 8 кл.
- Скачать:
- Подписи к слайдам:
- Средняя линия трапеции
- Понятие средней линии трапеции
- Теорема о средней линии трапеции
- Примеры задач на понятие средней линии трапеции
- Готовые работы на аналогичную тему
- 🔥 Видео
Видео:Теорема о средней линии трапецииСкачать

Свойства средней линии трапеции
- Длина средней линии равна половине суммы длин ее оснований:
Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

Доказательство теоремы о средней линии трапеции
Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
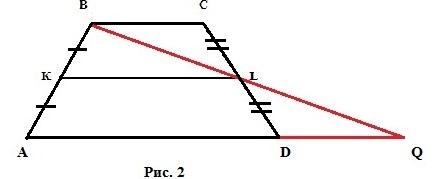
Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.
Рассмотрим полученные треугольники LBC и LQD:
- По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD, так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.
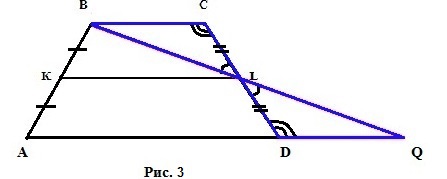
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:
- KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
- KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC.
Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:
Понравилась статья, расскажите о ней друзьям:
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Научная работа по теме «Средняя линия трапеции (несколько способов доказательств)», 8 кл.
Данная научная работа посвящена средней линии трапеции. Приведено 7 способов доказательств теоремы, исключая доказательство с помощью векторов, приведенное в учебнике Л.С. Атанасяна «Геометрия 7-9 классы». При доказательстве теоремы о средней линии трапеции показаны значения других теорем: теоремы о средней линии треугольника, признаков равенства треугольников, теоремы о параллельности прямых, а также следствие из аксиомы параллельных прямых, определения средней линии треугольника, признаки и определение параллелограмма, определение вертикальных углов и их свойств, свойства углов, образованных при пересечении параллельных прямых секущей. При доказательстве способа 5 доказывается единственность точки. В ходе доказательств данной теоремы использовались аналитический и синтетический методы доказательства теорем.
Видео:ТРАПЕЦИЯ теорема о средней линии Атанасян 9 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Научная работа «Средняя линия трапеции (несколько способов доказательств)», 8 кл. | 2.79 МБ |
| Презентация к научной работе «Средняя линия трапеции (несколько способов доказательств)», 8 кл. | 1.41 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
Видео:Теорема о средней линии трапецииСкачать

Подписи к слайдам:
МАТЕМАТИКА Средняя линия трапеции (несколько способов доказательства) Выполнила: Гаврилова Алиса Константиновна , обучающая 8-А кл. БОУ г. Омска «СОШ № 148» Руководитель работы: Яцюк Клавдия Васильевна , учитель математики БОУ г. Омска «СОШ № 148» ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ Г. ОМСКА бюджетное общеобразовательное учреждение города Омска «Средняя общеобразовательная школа № 148» Омск, 2012
Объект исследования: трапеция, средняя линия трапеции. Цель: показать, что доказательство теоремы о средней линии трапеции с помощью векторов, приведённое в учебнике Л.С. Атанасяна «Геометрия 7-9 классы» не является единственным, что существуют и другие способы доказательства. Задачи: Изучение научной и учебной литературы по заданной теме. Привести другие способы доказательства теоремы о средней линии трапеции. При доказательстве этой теоремы показать значение других теорем: признаков равенства треугольников, теоремы о параллельности прямых, теоремы о средней линии треугольника, а также следствие из аксиомы параллельных прямых, и определение средней линии треугольника и средней линии трапеции, признаки и определение параллелограмма. Методы исследования: применение аналитического и синтетического методов доказательства теорем.
А можно ли доказать? Теорема – математическое утверждение, истинность которого установлена путем доказательства [3]. Классическая теорема состоит из двух частей: из условия и заключения. Условие обыкновенно начинается со слова «если», а заключение со слова «то». Исходная теорема называется прямой теоремой Обратная теорема — если в исходной теореме условие сделать заключением, а заключение – условием. Если верна прямая теорема, то обратная теорема может быть неверной Взаимно обратные теоремы — если верны прямая и обратная теоремы Доказательством называется конечная последовательность формул, каждая из которых либо является аксиомой, либо получается из некоторых предыдущих формул этой последовательности по одному из правил вывода [3].
Теоретическая часть Средней линией треугольника называется отрезок, соединяющей середины двух его сторон. Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Два угла называются вертикальными , если стороны одного угла являются продолжением сторон другого. вертикальные. Прямые a и b параллельны, с –секущая. Пары углов: называются накрест лежащими. Свойство вертикальных углов . Вертикальные углы равны
Следствие 2° из аксиомы параллельных. Если две прямые параллельны третьей прямой, то они параллельны. Теорема о средней линии треугольника. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Второй признак равенства треугольников. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Признак параллельности двух прямых. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Признак параллелограмма 1° . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 1 . Доказательство . 1. Для доказательства из вершины B через точку N проведём прямую BN до пересечения этой прямой с продолжением основания AD в точке . 2. Рассмотрим ∆ BCN и (как вертикальные) (как накрест лежащие при пересечении параллельных прямых BC и А B секущей CD ); CN = ND ( по построению) 3. ∆ BCN = ( По второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам). => BC = и BN = . 4. По построению MB = AM . Значит, средняя линия трапеции MN является средней линией . По теореме о средней линии треугольника MN II => MN II AD , а AD II BC (по определению трапеции), то MN II BC ( следствие 2 из аксиомы параллельных прямых)(Если две прямые параллельны третье прямой, то они параллельны) и отрезок Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С )
Доказательство . 1. Для доказательства возьмём на основании AD точку Е . Из точки Е через точки М и N проведём прямые EM и EN до пересечения этих прямых с продолжением основания BC в точках О и Р соответственно. 2. Рассмотрим ∆BOM и ∆MAE . AM = MB (по построению); (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых OP и AD секущей АВ ) => ∆BOM = ∆MAE (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам) => OB = AE и OM = ME . Аналогично доказывается равенство треугольников PNC и DEN => PC = DE ; PN = NE . 3. Значит MN также является средней линией треугольника POE . По теореме о средней линии треугольника: MN || OP, а BC || AD (по определению трапеции). => MN || AD ( по следствию 2 из аксиомы параллельных прямых ( если две прямые параллельны третьей прямой, то они параллельны). И отрезок MN = OP = ( AD + BC ). Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 2 .
Доказательство . 1. На основании BC возьмём произвольную точку Е . Из точки Е через точки М и N проведём прямые EM и EN до пересечения этих прямых с продолжением основания AD в точках O и Р соответственно. 2. Рассмотрим ∆МВЕ и ∆АОМ . (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых ВС и ОР секущей АВ ); АМ=МВ (по построению). => ∆МВЕ =∆АОМ (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам) => ВЕ=ОА и ЕМ = ОМ . Аналогично доказывается равенство треугольников СЕ N и PND => EN = NP и EC = PD . 3. Значит MN также является средней линией треугольника POE . По теореме о средней линии треугольника MN || OP => MN || AD , а AD || BC (по определению трапеции) => MN || BC (по следствию 2 из аксиомы параллельных прямых (если две прямые параллельны третьей прямой, то они параллельны) и отрезок Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 3 .
Доказательство . 1. Для доказательства на продолжении основания А D откладываем отрезок DE=BC . Точку В соединяем с точкой Е . Прямая ВЕ проходит через точку N . В противном случае получается две середины: точки N и N 1 , а этого быть не может. 2. Рассмотрим ∆BCN и ∆DNE . BC=DE (по построению); , (как накрест лежащие углы при пересечении параллельных прямых ВС и АЕ секущими СD и ВЕ соответственно) => ∆BCN = ∆DNE по 2-му признаку равенства треугольников => CN=ND и BN=NE . 3. Рассмотрим ∆АВЕ . Т.к. BN=NE и АМ=МВ , то MN также является средней линией треугольника АВЕ . По теореме о средней линии треугольника (средняя линия треугольника параллельна одной из его сторон и равна её половине) MN || AE, => MN || AD, а AD || BC (по определению трапеции) => MN || BC (следствие 2 из аксиомы параллельных прямых) (если две прямые параллельны третьей прямой, то они параллельны) и Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 4 .
Доказательство . 1. Для доказательства на продолжении основания ВС отложим A 1 C=AD , а на AD отложим B 1 D=BC .Соединим точку А 1 с точкой В 1 . А также продолжим MN до пересечения этой прямой с прямой A 1 В 1 в точке М 1 . 2. Докажем, что точка M 1 является серединой A 1 В 1 .Соединим вершину В с В 1 и докажем, что BВ 1 проходит через точку N . Допустим, что BВ 1 проходит через точку N . Рассмотрим ∆ВСN и ∆B1ND . ; (как накрест лежащие при пересечении параллельных прямых BA 1 и АВ 1 секущими CD и ВВ 1 соответственно). ВС= B 1 D (по построению ). => ∆BCN=∆B 1 ND (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). => BN=B 1 N , CN = ND=> проходит через точку N . Рассмотрим ∆MBN и ∆M 1 B 1 N . (как вертикальные); ( как накрест лежащие углы при пересечении параллельных прямых АВ и А 1 В 1 секущей ВВ 1 ); BN= В 1 N ( по доказанному) => ∆MBN=∆M 1 В 1 N (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). => M 1 В 1 = MB . Так как AM=MB , то M 1 В 1 = AM .=> M 1 — середина стороны A 1 В 1 . Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 5 .
Доказательство продолжение . 3. Рассмотрим четырёхугольник ABA 1 В 1 . BA 1 = AВ 1 (по построению); BA 1 || AВ 1 (так как BC || AD по определению трапеции). => AB A 1 В 1 – параллелограмм. (по признаку параллелограмма 1° (если в четырёх угольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм). Рассмотрим трапецию ABCD и A 1 В 1 DC . Они равны по построению. Значит MN=M 1 N => 4. По построению AB || A 1 В 1 => AM || B 1 M 1 и M B || A 1 M 1 . Т.к. трапеции ABCD и A 1 В 1 DC равны, то => MB= M 1 B 1 и AM=A 1 M 1 ,а так как АМ=МВ и А 1 М 1 = M 1 B 1 (по построению), то АМ=МВ= A 1 M 1 = M 1 B 1 . Значит четырёхугольники МВA 1 M 1 и АМ M 1 B 1 – параллелограммы (по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм).=> BА 1 ||MM 1 и BА 1 =MM 1 ; MM 1 =AВ 1 и MM 1 || AВ 1 ( как противоположные стороны параллелограмма). => MN || BC ; BC||AD => MN || AD ( по следствию два из аксиомы параллельных прямых (если две прямые параллельны третье прямой, то они параллельны). 5. Т.к. BA 1 = MM 1 , то т.е. А т.к. BA 1 = ВС+С A 1 , а CA 1 = AD (по построению), то BA 1 =ВС+ AD . Значит Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 5 .
Доказательство . 1. Для доказательства на продолжении основания AD отложим отрезок DE = BC . А также на продолжении средней линии MN трапеции ABCD отложим отрезок NK = MN . Трапеции MBCN и KNDE будут равны (по построению). 2. Т.к. MBCN = KNDE , то КЕ=МВ , МВ=АМ => АМ=КЕ . КЕ|| MB => KE || AM . Значит по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник АМКЕ – параллелограмм. => MK = AE и MK || AE (как противоположные стороны параллелограмма) => MN || AD , а AD || BC (по определению трапеции) => MN || BC (по следствию два из аксиомы параллельных прямых)(если две прямые параллельны третьей прямой, то они параллельны). 3. Рассмотрим параллелограмм АМКЕ . MN = NK , а так как MK = MN + NK =2 MN , то Т.к. MK = AE , то А т.к. AE=AD+DE и DE=BC ( по построению ), то AE=AD+BC => , т . е . Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 6 .
Доказательство . 1. Для доказательства через точку N проведём прямую EK || AB до пересечения этой прямой с продолжением основания ВС в точке Е и с основанием AD в точке К . 2. Рассмотрим ∆NEC и ∆NKD ; CN=ND (по построению), (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых BE и AD секущей CD ). =>∆NEC=∆NKD (по второму признаку равенства треугольников( по стороне и двум прилежащим к ней углам). => CE=KD и EN=NK . 3. Рассмотрим четырёхугольник ABEK. AB || EK (по построению), BC || AD , => BE||AD (по определению трапеции) => четырёхугольник АВЕК – параллелограмм (по определению параллелограмма).=> AB=EK и AB || EK (как противоположные стороны параллелограмма). И EN=NK (из равенства треугольников NEC и NKD (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам), а AM=MB (по построению). Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 7 .
Доказательство продолжение . 4. Рассмотрим четырёхугольники MBEN и AMNK . MB = EN и MB|| EN . Значит по первому признаку параллелограмма (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник MBEN – параллелограмм. AM=NK и AM||NK => по первому признаку параллелограмма (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник AMNK – параллелограмм. => MN=BE и MN=AK ; MN||BE и MN||AK (как противоположные стороны параллелограмма) => MN|| BC и MN|| AD . 5. Т . к . MN= BE, MN=AK , то MN=BC+CE . Сложив эти равенства, получаем: AD = AK + KD , а т.к. KD = CE , то AD = AK + CE => 2 MN = AD + BC . Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 7 .
Заключение Поставленная цель достигнута. Теорема о средней линии трапеции доказана семью способами с помощью признаков равенства треугольников, теорем о параллельности прямых, теоремы о средней линии треугольника, признаков и определения параллелограмма, а также следствий из аксиомы параллельных прямых и определений средней линии треугольника, средней линии трапеции. Выше изложенные доказательства и моделирование ситуаций помогут мне при решении задач.
Литература Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов средней школы». М.: Издательство «Просвещение» 2010 г. Далингер В.А. «Методика работы над формулировкой и доказательством и закреплением теоремы». Омск. Издательство «ОмИПКРО» 1995 г. Математическая энциклопедия под редакцией И.М. Виноградова. М.: Изд. Советская Энциклопедия, 1984 г, том 4 и том 5. Погорелов А.В. «Геометрия 7-11. Учебник для 7-11 классов средней школы». М.: Издательство «Просвещение» 2010 г. Энциклопедия для детей. Том 11. Математика/ Глав. ред. М.Д. Аксенова. – М.: Аванта+, 2000 г. Якушева Г.М. «Математика. Справочник школьника». М.: Издательство «Слово» 1995 г. Якушева Г.М. «Решение задач по математике. Справочник школьника». М.: Издательство «Слово». 1996 г.
Видео:Геометрия 9 класс. Средняя линия трапецииСкачать

Средняя линия трапеции
Вы будете перенаправлены на Автор24
Видео:умножение ВЕКТОРА на число + теорема о средней линии ТРАПЕЦИИСкачать

Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Видео:Геометрия 9 класс (Урок№5 - Средняя линия трапеции.)Скачать

Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её векторным методом.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac$.
Рассмотрим вектор $overrightarrow$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Из этого же равенства (так как $overrightarrow$ и $overrightarrow$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Примеры задач на понятие средней линии трапеции
Боковые стороны трапеции равны $15 см$ и $17 см$ соответственно. Периметр трапеции равен $52 см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
[15 см+17 см=32 см]
Следовательно, так как периметр равен $52 см$, сумма оснований равна
[52 см-32 см=20 см]
Значит, по теореме 1, получаем
Ответ: $10 см$.
Готовые работы на аналогичную тему
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
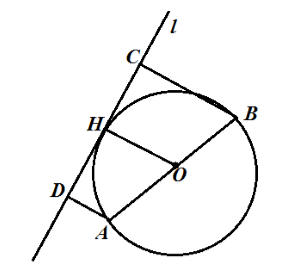
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9 см$ и $BC=5 см$. Проведем радиус $OH$ (рис. 2).
Так как $AD$ и $BC$ — расстояния до касательной, то $ADbot l$ и $BCbot l$ и так как $OH$ — радиус, то $OHbot l$, следовательно, $OH|left|ADright||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
[d=2OH=2cdot 7 см=14 см.]
Ответ: $14$ см.
Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.
Доказательство.
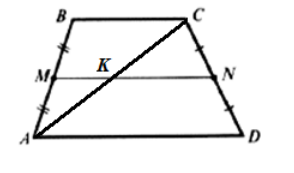
Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ — точку пересечения средней линии с этой диагональю (Рис. 3).
Докажем, что $AK=KC$.
Так как $MN$ — средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ — средняя линия треугольника $ABC$. Значит $AK=KC$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 04 2021
🔥 Видео
88. Средняя линия трапецииСкачать

Средняя линия трапеции и её свойства. Векторы на плоскости. Геометрия 8-9 классСкачать

Трапеция. Средняя линия трапеции.Скачать
Средняя линия. Теорема о средней линии треугольникаСкачать

Теорема о средней линии треугольникаСкачать

Средняя линия трапеции | Геометрия 7-9 класс #84 | ИнфоурокСкачать

Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

Теорема о средней линии трапецииСкачать

Теорема о средней линии трапецииСкачать

ТРАПЕЦИЯ. СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ. Видеоурок | ГЕОМЕТРИЯ 9 классСкачать

Свойство средней линии трапеции доказательствоСкачать