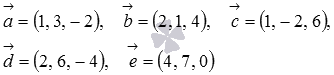В этой статье мы поговорим о компланарности векторов. Сначала вспомним определение компланарности и получим необходимое и достаточное условие компланарности трех векторов в трехмерном пространстве. Далее разберемся с задачей исследования системы из n векторов на компланарность, рассмотрим решения характерных примеров.
Навигация по странице.
- Необходимое и достаточное условие компланарности трех векторов.
- Исследование системы векторов на компланарность, примеры и решения.
- Компланарность векторов. Условия компланарности векторов.
- Условия компланарности векторов
- Примеры задач на компланарность векторов
- Доказать, что 4 точки лежат в одной плоскости : A( 1, 2, — 1) B(0, 1, 5) C( — 1, 2, 1) D(2, 1, 3)?
- На плоскости дано 7 точек, из которых никакие три не лежат на одной прямой?
- На плоскости отметили несколько точек, никакие три из них не лежат на одной прямой?
- Прямые ЕМ и КМ не лежат в одной плоскости?
- СРОЧНО?
- Определить, находятся ли точки , , на одной плоскости?
- Сравните перпендикуляр и наклонную проведенные из одной точки к плоскости?
- Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые?
- Точки А В С лежат на одной прямой АВ = x AC = x — 2 Может ли точка В лежать между точками А и С?
- На одной координатной плоскости построить параболу у = х² и прямую у = 3?
- Точки А, В, С, Д не лежат в одной плоскости?
Необходимое и достаточное условие компланарности трех векторов.
Напомним определение компланарных векторов.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два вектора 
и 
трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы и соответственно. Проведем через начало вектора прямую b1 , параллельную прямой b , а через начало вектора прямую a1 , праллельную прямой a . Плоскости, образуемые прямыми a и b1 , а так же прямыми b и a1 , параллельны по построению, а векторы и принадлежат им. Следовательно, векторы и компланарны.
А как же определить, являются ли три вектора компланарными?
Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
Для компланарности трех векторов 
и 
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Пусть 
, докажем что векторы и компланарны.
Так как 
, то векторы 
и перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор перпендикулярен и вектору и вектору . Следовательно, векторы и компланарны, так как перпендикулярны одному вектору .
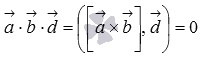
Пусть теперь векторы и компланарны, докажем равенство нулю смешанного произведения 
.
Так как векторы и компланарны, то вектор перпендикулярен каждому из них, следовательно, скалярное произведение вектора на равно нулю, что означает равенство нулю смешанного произведения .
Итак, теорема полностью доказана.
Покажем применение доказанного условия компланарности трех векторов к решению задач.
Компланарны ли векторы 
, заданные в прямоугольной системе координат.
Вычислим их смешанное произведение по координатам:
Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.
Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов 
и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.
Принадлежат ли точки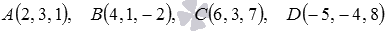 
одной плоскости?
Найдем координаты векторов (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):
Теперь вычисляем смешанное произведение этих векторов
Так как смешанное произведение векторов отлично от нуля, то векторы не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.
Исследование системы векторов на компланарность, примеры и решения.
А как же быть, если требуется установить компланарность системы векторов, число векторов которой больше трех?
Давайте ответим на этот вопрос и получим условие компланарности системы из n векторов трехмерного пространства.
В предыдущем пункте мы показали, что для компланарности трех векторов и необходимо и достаточно равенство нулю их смешанного произведения: . Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов и , то условие компланарности можно записать в виде 
. Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов и , меньше трех.
Обобщив последнее утверждение, мы получим необходимое и достаточное условие компланарности системы из n векторов трехмерного пространства: для компланарности системы из n векторов трехмерного пространства необходимо и достаточно, чтобы ранг матрицы, строками которой являются координаты векторов системы, был меньше трех.
Компланарны ли векторы
Составим матрицу, строками которой примем координаты данных векторов
Сразу легко отыскать минор второго порядка, отличный от нуля,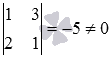 
.
Переберем окаймляющие его миноры третьего порядка:
Все они равны нулю, следовательно, ранг матрицы равен двум, поэтому, векторы заданной системы векторов компланарны в силу выполнения необходимого и достаточного условия компланарности.
Компланарность векторов. Условия компланарности векторов.
 |
| рис. 1 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
Примеры задач на компланарность векторов
Решение: найдем смешанное произведение векторов
| a · [ b × с ] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.
Решение: найдем смешанное произведение векторов
| a · [ b × с ] = | 1 | 1 | 1 | = |
| 1 | 3 | 1 | ||
| 2 | 2 | 2 |
= 1·2·3 + 1·1·2 + 1·1·2 — 1·2·3 — 1·1·2 — 1·1·2 = 6 + 2 + 2 — 6 — 2 — 2 = 0
Ответ: вектора компланарны так, как их смешанное произведение равно нулю.
Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования
 | 1 | 1 | 1 |  |
| 1 | 2 | 0 | ||
| 0 | -1 | 1 | ||
| 3 | 3 | 3 |
из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3
к 3-тей строке добавим 2-рую
Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.
Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.
Доказать, что 4 точки лежат в одной плоскости : A( 1, 2, — 1) B(0, 1, 5) C( — 1, 2, 1) D(2, 1, 3)?
Алгебра | 10 — 11 классы
Доказать, что 4 точки лежат в одной плоскости : A( 1, 2, — 1) B(0, 1, 5) C( — 1, 2, 1) D(2, 1, 3).
AB = ( — 1 ; — 1 ; 6) AC = ( — 2 ; 0 ; 2) AD = (1 ; — 1 ; 4)
теперь аналогично к предыдущему заданию составляешь определитель и вычисляеш его, получается Δ = 0 и значит точки лежат в одной плоскости.
На плоскости дано 7 точек, из которых никакие три не лежат на одной прямой?
На плоскости дано 7 точек, из которых никакие три не лежат на одной прямой.
Сколько различных треугольников можно построить с вершинами в этих точках?
На плоскости отметили несколько точек, никакие три из них не лежат на одной прямой?
На плоскости отметили несколько точек, никакие три из них не лежат на одной прямой.
Через каждые две точки провели прямую.
Сколько точек было отмечено, если всего было проведено 28 прямых?
Прямые ЕМ и КМ не лежат в одной плоскости?
Прямые ЕМ и КМ не лежат в одной плоскости.
Могут ли прямые ЕМ и NK пересекаться?
СРОЧНО?
1! Лежат ли точки A(1, 2, — 1), B(0, 1, 5), C( — 1, 2, 1) и D(2, 1, 3) в одной плоскости?
Определить, находятся ли точки , , на одной плоскости?
Определить, находятся ли точки , , на одной плоскости.
Если это так, написать уравнение этой плоскости.
Сравните перпендикуляр и наклонную проведенные из одной точки к плоскости?
Сравните перпендикуляр и наклонную проведенные из одной точки к плоскости.
Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые?
Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые.
Точки А В С лежат на одной прямой АВ = x AC = x — 2 Может ли точка В лежать между точками А и С?
Точки А В С лежат на одной прямой АВ = x AC = x — 2 Может ли точка В лежать между точками А и С?
На одной координатной плоскости построить параболу у = х² и прямую у = 3?
На одной координатной плоскости построить параболу у = х² и прямую у = 3.
При каких значениях х точки параболы лежат выше прямой?
Точки А, В, С, Д не лежат в одной плоскости?
Точки А, В, С, Д не лежат в одной плоскости.
Докажите что : а) вектор АВ — СД = АС — ВД ; б) |1 / 2(вектор АД — АВ) = |1 / 2( вектор СВ — СД)|.
Вы открыли страницу вопроса Доказать, что 4 точки лежат в одной плоскости : A( 1, 2, — 1) B(0, 1, 5) C( — 1, 2, 1) D(2, 1, 3)?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.