Для чтобы прямые а и б были параллельны нужно чтобы

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

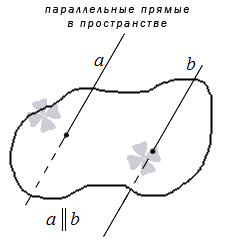
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

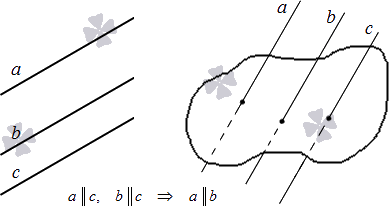
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

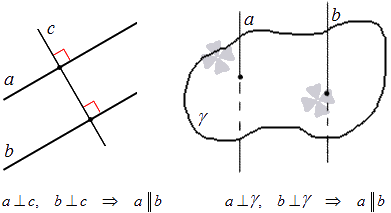
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;

и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

1. Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:

A 1 = t · A 2 B 1 = t · B 2

1. Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) соответственно, а условие параллельности запишем так:

k 1 = t · k 2 — 1 = t · ( — 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

1. Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .

Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:

a x = t · b x a y = t · b y

Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0

Мы видим, что n a → = ( 2 , — 3 ) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:

2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?

Решение

Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:

x 1 = y — 4 2 ⇔ 1 · ( y — 4 ) = 2 x ⇔ y = 2 x + 4

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , — 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:

n a → , b → = 2 · 1 + ( — 1 ) · 2 = 0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , — 3 ) и ( 2 , 0 , — 6 ) .

1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Видео:№44. Прямые ОВ и CD параллельные, а ОА и CD — скрещивающиеся прямые.Скачать

Для того, чтобы прямые а и б были параллельными, нужно чтобы ?

Геометрия | 5 — 9 классы

Для того, чтобы прямые а и б были параллельными, нужно чтобы :

то есть 2 вариант ответа.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Докажите что если две прямые параллельно третьей прямой то они параллельны?

Докажите что если две прямые параллельно третьей прямой то они параллельны.

Видео:№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать

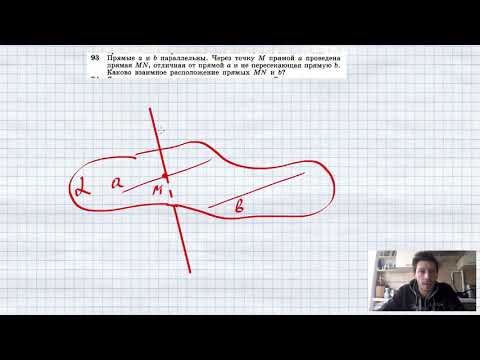
Прямая n параллельна прямой m параллельна плоскости а?

Прямая n параллельна прямой m параллельна плоскости а.

Следует ли из этого, что прямая n параллельна плоскости а.

Видео:Параллельность прямых. 10 класс.Скачать

НУЖНО ТОЛЬКО 4 И 6 РИСУНОК?

НУЖНО ТОЛЬКО 4 И 6 РИСУНОК.

ПАРАЛЛЕЛЬНЫ ЛИ ПРЯМЫЕ А И Б?

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

Нужно указать пару(пары)параллельных прямых(отрезков) и доказать их параллельность?

Нужно указать пару(пары)параллельных прямых(отрезков) и доказать их параллельность!

Видео:Параллельные прямые (задачи).Скачать

Подскажите пожалуйста, какой признак параллельных прямых тут использовать нужно?

Подскажите пожалуйста, какой признак параллельных прямых тут использовать нужно?

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и ко второй прямой (нужно доказать)?

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и ко второй прямой (нужно доказать).

Видео:1 признак параллельности прямых.Скачать

Помогите?

Нужно найти параллельные прямые!

Видео:Параллельные прямые. 6 класс.Скачать

Помогите ответить пожалуйста?

Помогите ответить пожалуйста!

1. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны : 1) определение параллельных прямых 2) признак параллельности двух прямых 3) аксиома параллельности двух прямых 4) теорема параллельных прямых 2.

Если две прямые параллельные третьей прямой, то они параллельны.

Это утверждение есть_______.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Параллельные прямые ?

Нужна помощь очень !

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Если прямая а параллельна прямой б, и прямая а параллельно прямой с?

Если прямая а параллельна прямой б, и прямая а параллельно прямой с.

То что можно сказать о прямых б и с.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Для того, чтобы прямые а и б были параллельными, нужно чтобы ?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Рассмотрим треугольник АDB и треугольник ACB : угол CA = углу ABD , угол АBD = углу DBA Сторона AB — общая . Значит треугольник ACB = треугольнику BDA по второму признаку равенства треугольников . Тогда AC = BD = 13см.

Так как∆АВС и∆АДС равнобедренные, то АД = ДС АВ = ВС Что бы получить АБД и СВД нужно провести от точки Д до точки Б прямую, она же будет общей стороной. Значит по третьему признаку равенства треугольников∆АВД = ∆СВД.

Дано : ΔCBDостроугольный и равнобедренный ; СB = CD ; BB₁┴CD ; DD₁┴CB ; ∠BPD = 126°( P — точка пересечения высотBB₁ иDD₁). — — — — — — — — — — — — — — — — — — — ∠С — ? , ∠B = ∠D — ? * * * иначе ∠СBD = ∠СDB — ? * * * ∠С + ∠B + ∠D = 180 ; ΔCBDравно..

23 вроде. Ээээээээээээээээээээээээээээххххххххххххххххххххххххэхххээхэхэхэхэ.

Нужен циркуль и линейка 1. Чертим луч ОО1. 2. Строим перпендикуляр к лучу ОО1. 3. Точка пересечения лучей будет точка А. 4. Отложим от точки А влево катет равный b, и место пересечения будет точка С 5. Отложим от точки А катет равный a вверх, по..

Пусть прямые a и b одновременно параллельны прямой c. Допустим, что a не параллельна b, тогда прямая a пересекается с прямой b в некоторой точке М, не лежащей на прямой c по условию. Следовательно, мы имеем две прямые a и b, проходящие через точку ..

ОДЗ х не равен 4 Сокращаем дробь на (х — 4) строим график гиперболы у = 1 — 1 / х Выкалываем из графика точку (4 ; 0. 75).

Учебник геометрии, посмотри и все поймешь.

Радиус окружности, описанной около правильного (равностороннего) треугольника, равен двойному радиусу окружности, вписанной в этот треугольник. R = 2r , где R — радиус описанной окружности, r — радиус вписанной окружности R = 2 * 2 = 4 (cм) Радиусок..

Находим вторую точку (правую) криволинейной трапеции, приравняв уравнение значению у = 0, 5. 1 / х = 0, 5, х = 1 / 0, 5 = 2. Из этой трапеции вычитается нижняя её часть от 0 до 0, 5. Тогда площадь S равна .

Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

Урок на тему Повторение. Параллельные прямые

Видео:Параллельные прямые - геометрия 7 классСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ТЕМА . Повторение. Параллельные прямые

Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.

Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности.

Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов.

Личностные: осознают важность и необходимость изучения предмета

Фронтальная (Ф); индивидуальная (И)

• Задания для теста.

• Задания для фронтальной работы

I этап. Актуализация опорных знаний учащихся

Задания для математического диктанта

Привести в систему
теоретические знания по теме

1. Проверка домашнего задания. Обсуждение вопросов учащихся.

2. Тест на проверку теоретических знаний (самостоятельное выполнение с последующим обсуждением)
(см. Ресурсный материал)

II этап. Решение задач

Совершенствовать
навыки решения задач

Решение задач (устно) .

1. Найти: параллельные прямые. 2. Найти: параллельны ли прямые а и b ?

Ответ : а || с . Ответ : да.

3. Найти: параллельны ли прямые а и b ? 4. Дано: а || b .

Ответ : нет. Ответ :  1 = 100°,  2 = 80°.

Ответ :  1 = 50°,  2 = 130°. Ответ :  1 = 130°,  2 = 50°.

7. Найти:  1,  2. 8. Найти:  1.

Ответ :  1 = 70°,  2 = 70°. Ответ :  1 = 76°.

9. Найти:  1. 10. Найти:  3.

Ответ :  1 = 34°. Ответ :  3 = 80°.

11. Найти:  МОЕ . 12. Найти: параллельны ли АВ и СD ?

Ответ :  МОЕ = 90°. Ответ : да.

13. Дано: а || b , DE – секущая, DE = 3,9 см. 14. Дано:  2 –  1 = 44°.

Найти: MN . Найти:  1,  2.

Ответ : MN = 7,8 см. Ответ :  1 = 68°,  2 = 112°.

Ответ :  ABC = 58°. Ответ :  EMN = 106°.

Ответ :  ECP = 150°. Ответ :  ACK = 84°

III этап. Итоги урока. Рефлексия

– Сформулируйте аксиому параллельности.

– Сформулируйте признаки параллельности прямых.

– Оцените свою работу на уроке

(И) Домашнее задание: повторить главу IV (§ 1, 2, 3), вопросы 1–18 (без доказательства); записать полное решение задач 1–18 (для выполнения этого задания можно класс разбить на варианты)

а) а || b ; б) a  b ; в) ответы а) и б) неверны.

a) a  b ; б) а || b ; в) ответы а) и б) неверны.

3. Рис. 1. Если а || b , с – секущая, то:

a)  2 +  3 = 180°; б)  5 =  2; в)  1 +  3 = 180°.

4. Рис. 2. Для того чтобы прямые а и b были параллельными, нужно, чтобы:

a)  1 +  4 = 180°; б)  1 =  2; в)  3 =  2.

5. Рис. 3. PR || QD , так как:

a)  3 =  7; б)  8 =  4; в)  2 =  6.

Рис. 1 Рис. 2 Рис. 3

6. Один из углов при пересечении двух параллельных прямых третьей равен 52°. Остальные углы равны:

а) 52° и 132°; б) 52° и 128°; в) 52°.

8. Прямая АВ пересекает параллельные прямые РK и MN ( A  РK , В  MN ). Сумма углов РАВ и МВА равна 116°. Какие из следующих высказываний верны?

а) Точки K и М лежат в одной полуплоскости относительно прямой АВ .

б) Точки Р и N лежат в разных полуплоскостях относительно прямой АВ .

в) Сумма углов РАВ и NBA равна 180°.

9. Прямая MN является секущей для прямых АВ и CD ( М  АВ , N  CD ). Угол AMN равен 78°. При каком значении угла CNM прямые АВ и CD могут быть параллельны?

а) 102°; б) 12°; в) 78°; г) 78° и 102°.

Ответы : 1 – а; 2 – б; 3 – в; 4 – в; 5 – в; 6 – б; 7 – б; 8 – а, в; 9 – г.

Видео:Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Булдакова Любовь ПетровнаНаписать 2711 15.05.2018

Номер материала: ДБ-1596820

15.05.2018 419

14.05.2018 2780

30.04.2018 296

24.04.2018 896

17.04.2018 4996

15.04.2018 230

15.04.2018 174

08.04.2018 2457

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔍 Видео

Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать