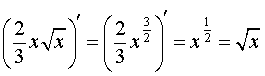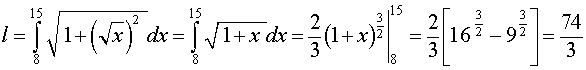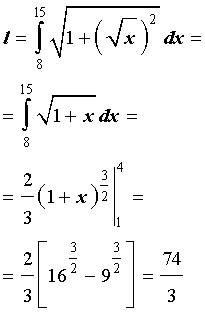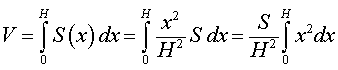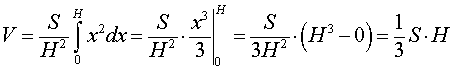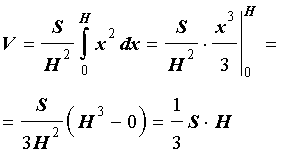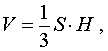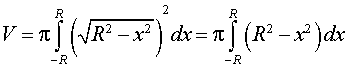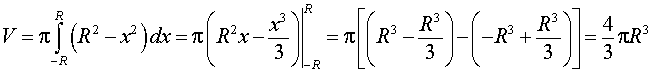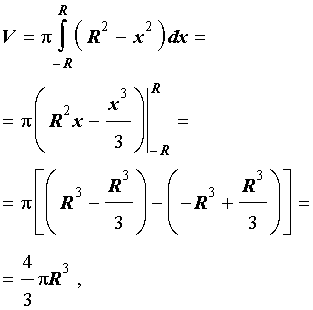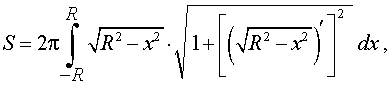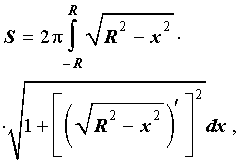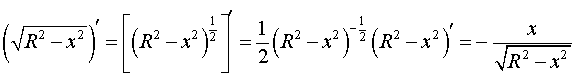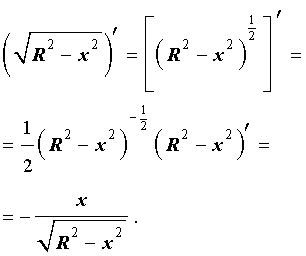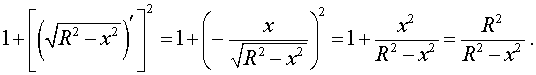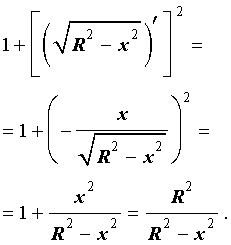Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла |
 Примеры решения задач на вычисление площадей фигур на плоскости Примеры решения задач на вычисление площадей фигур на плоскости |
 Пример решения задачи на вычисление длины дуги кривой на плоскости Пример решения задачи на вычисление длины дуги кривой на плоскости |
 Вывод формул для объема пирамиды и для объема шара Вывод формул для объема пирамиды и для объема шара |
 Вывод формулы для площади сферы Вывод формулы для площади сферы |
- Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
- Примеры решения задач на вычисление площадей фигур на плоскости
- Пример решения задачи на вычисление длины дуги кривой на плоскости
- Вывод формул для объема пирамиды и для объема шара
- Вывод формулы для площади сферы
- Приложения определенного интеграла
- Вычисление площади плоской фигуры.
- Плоская фигура и ее площадь.
- Площадь криволинейной трапеции.
- Площадь криволинейного сектора.
- Вычисление объема тела.
- Тело и его объем.
- Объем тела вращения.
- Объем тела с заданными площадями поперечных сечений.
- Вычисление длины дуги кривой.
- Вычисление площади поверхности вращения.
- Применение определенного интеграла при решении физических задач.
- Как найти длину дуги кривой с помощью интеграла
- Вычисление длины дуги кривой, заданной в прямоугольных координатах
- Вычисление длины дуги кривой, заданной параметрически
- Вычисление длины дуги кривой, заданной в полярных координатах
- 🔍 Видео
Видео:Длина окружности. Математика 6 класс.Скачать

Формулы для вычисления площадей фигур на плоскости, длин дуг кривых на плоскости, площадей поверхностей тел вращения и объемов тел с помощью определенного интеграла
В данном разделе справочника приведена таблица, содержащая формулы, с помощью которых можно вычислить:
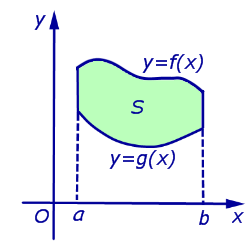
Площади криволинейных трапеций различного вида (площади фигур, ограниченных графиками функций);
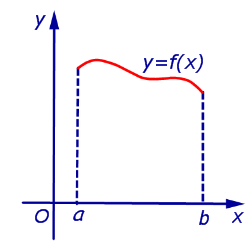
Длины дуг кривых на плоскости;
Объемы тел, если известны площади их поперечных сечений;
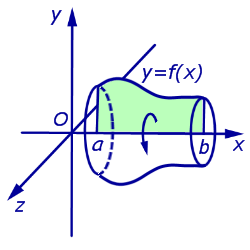
Объемы тел, полученных при вращении криволинейных трапеций вокруг оси абсцисс Ox ;
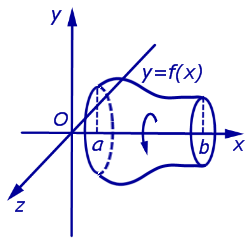
Площади поверхностей тел, полученных при вращении графиков функций вокруг оси абсцисс Ox .
| Рисунок | Формула | Описание | |||||||
 | 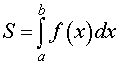 | ||||||||
 |  | ||||||||
 | 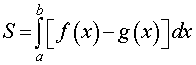 | ||||||||
 | 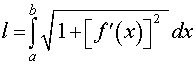 | ||||||||
 | 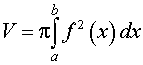 | ||||||||
 | 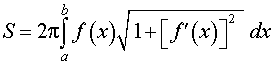 |
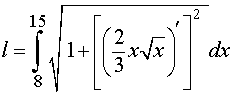 | (1) |
Подставим найденную производную в формулу (1), а затем вычислим полученные интегралы при помощи таблицы неопределенных интегралов и формулы Ньютона — Лейбница:
Ответ .
Видео:Длина эллипса и разложение в ряд для эллиптического интегралаСкачать

Вывод формул для объема пирамиды и для объема шара
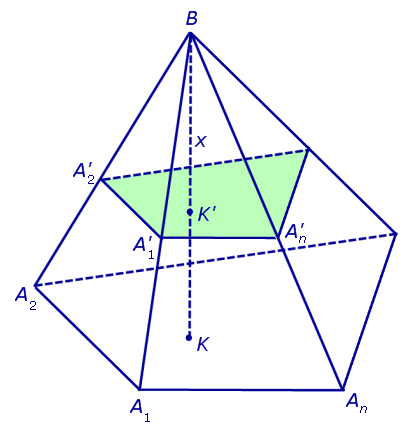
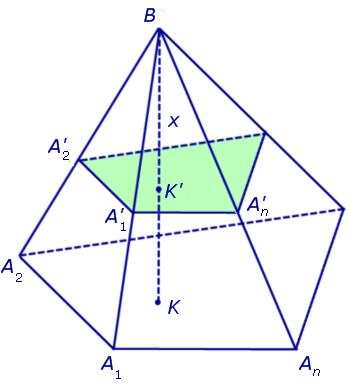
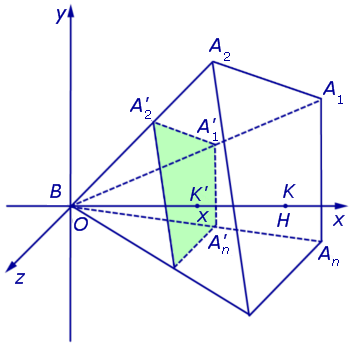
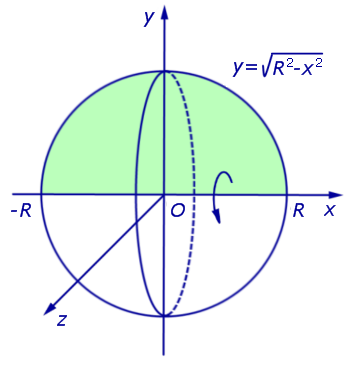
Решение . Рассмотрим произвольную n — угольную пирамиду BA1A2 . An с вершиной B, высота BK которой равна H, а площадь основания A1A2 . An равна S. Обозначим через S (x) площадь сечения 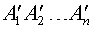
Поскольку многоугольники 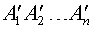
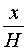
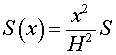 | (2) |
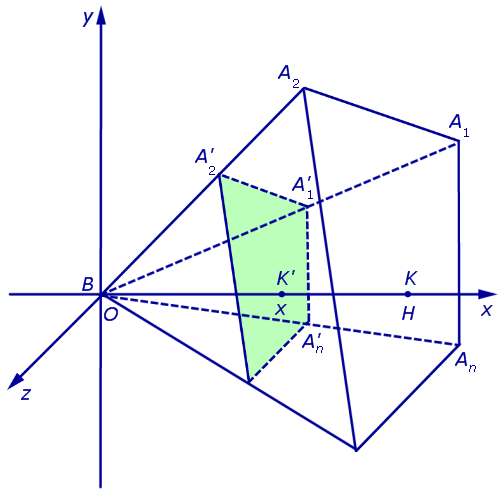
Рассмотрим теперь в пространстве систему координат Oxyz и расположим нашу пирамиду BA1A2 . An так, чтобы ее вершина B совпала с началом координат O, а высота пирамиды BK оказалась лежащей на оси Ox (рис. 5).
Тогда сечение 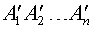
Итак, мы получили формулу для объема пирамиды
котрой пользовались в различных разделах справочника.
Замечание . Совершенно аналогично выводится формула для объема конуса. Формулы для объема прямой призмы объема прямой призмы и для объема цилиндра вывести таким способом еще проще, поскольку у них все сечения, перпендикулярные высоте, равны между собой. Мы рекомендуем провести эти выводы читателю самостоятельно в качестве полезного упражнения.
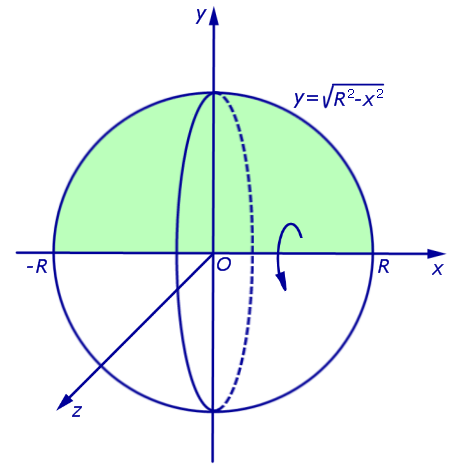
Пример 5 . Вывести формулу для объема шара радиуса R, воспользовавшись формулой для вычисления объема тела вращения.
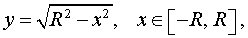 | (3) |
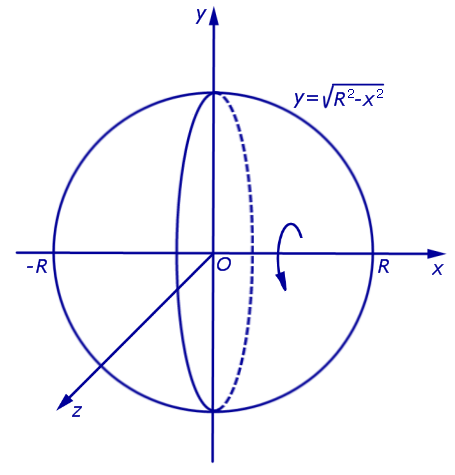
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O. Шар радиуса R получается в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции (3) и ограниченной снизу отрезком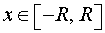
что и должно было получиться.
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Вывод формулы для площади сферы
Решение . Снова рассмотрим функцию
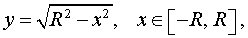 | (4) |
графиком которой является верхняя полуокружность радиуса R с центром в начале координат O (рис. 7).
Поскольку сфера радиуса R получается в результате вращения вокруг оси Ox графика функции (4), то в соответствии с формулой для вычисления площади поверхности тела вращения получаем
Подставим найденную производную в выражение, стоящее под знаком квадратного корня:
Таким образом, подынтегральная функция принимает вид:
Видео:Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

Приложения определенного интеграла
Видео:Длина окружности. 9 класс.Скачать

Вычисление площади плоской фигуры.
Плоская фигура и ее площадь.
Произвольное ограниченное множество точек плоскости будем называть плоской фигурой. Если плоскую фигуру можно представить как объединение конечного числа непересекающихся прямоугольников, то такую фигуру назовем клеточной. Подпрямоугольником будем понимать множество точек вида
$$
K = <(x, y): a_leq x leq b_, a_ leq y leq b_>nonumber
$$
или множество, получаемое из (K) удалением части границы (или всей границы) множества (K).
Площадью прямоугольника (K) назовем число ((b_-a_)(b_-a_)) независимо от того, принадлежат или не принадлежат множеству (K) его граничные точки, а площадью клеточной фигуры назовем сумму площадей прямоугольников, из которых составлена эта фигура.
Можно показать, что площадь клеточной фигуры не зависит от способа разбиения ее на прямоугольники. Нетрудно также убедиться в том, что площадь клеточной фигуры неотрицательна и обладает свойствами:
- аддитивности, то есть площадь объединения двух непересекающихся клеточных фигур равна сумме их площадей;
- инвариантности, то есть площади двух равных (конгруэнтных) клеточных фигур совпадают;
- монотонности, то есть если клеточные фигуры (G_) и (G_) таковы, что (G_ subset G_), то площадь фигуры (G_) не превосходит площади фигуры (G_).
Плоскую фигуру (G) назовем квадрируемой, если для любого (varepsilon > 0) найдутся клеточные фигуры (q) и (Q) такие, что
$$
q subset G subset Q,label
$$
$$
0 leq S(Q)-S(q) Теорема 1.
Для любой квадрируемой фигуры (G) число (S(G)) существует и единственно, причем
$$
S(G) = sup S(q) = inf S(Q).label
$$
(circ) Так как для любых клеточных фигур (q) и (Q), удовлетворяющих условию eqref, выполняется неравенство
$$
S(q) leq S(Q),nonumber
$$
то по теореме об отделимости существуют (sup S(q)) и (inf S(Q)) (супремум и инфимум берутся по всем клеточным фигурам, соответственно содержащимся в фигуре (G) и содержащим эту фигуру), причем
$$
S(q) leq sup S(q) leq inf S(Q) leq S(Q),label
$$
откуда
$$
S(q) leq sup S(q) leq S(Q),label
$$
Таким образом, число (S(G) = sup S(q)) удовлетворяет условию eqref.
Докажем единственность числа (S(G)). Предположим, что наряду с числом (S(G)) существует еще одно число (S'(G)), удовлетворяющее условию eqref, то есть
$$
S(q) leq S^(G) leq S(Q),label
$$
Тогда из eqref и eqref в силу свойств неравенств получаем, что
$$
|S(G)-S'(G)| leq S(Q)-S(q)label
$$
для любых клеточных фигур таких, что (q subset G subset Q). Так как (G) -квадрируемая фигура, то разность (S(Q)-S(q)) можно сделать сколь угодно малой в силу условия eqref, выбрав соответствующие фигуры (Q) и (q). Поэтому из eqref следует, что (S'(G) = S(G)). Таким образом, квадрируемая фигура (G) имеет площадь (S(G)), причем в силу eqref справедливо равенство eqref. (bullet)
Для того чтобы плоская фигура (G) была квадрируема, необходимо и достаточно, чтобы для любого (varepsilon > 0) существовали такие квадрируемые плоские фигуры (tilde) и (tilde
), что
$$
tilde subset G subset tilde
,quad 0 leq S(tilde
)-S(tilde
) Доказательство.
(circ) Необходимость условий eqref очевидна, так как по определению квадрируемой фигуры эти условия выполняются, если взять (tilde = q, tilde
= Q), где (q) и (Q) — клеточные фигуры, удовлетворяющие соотношениям eqref, eqref.
Докажем достаточность. Фиксируя произвольное число (varepsilon > 0), найдем в силу eqref такие квадрируемые плоские фигуры (tilde) и (tilde
), что
$$
tilde subset G subset tilde
, 0 leq S(tilde
)-S(tilde
) Замечание 2.
Можно доказать, что площадь квадрируемой фигуры обладает свойствами аддитивности, инвариантности и монотонности (см. замечание 1).
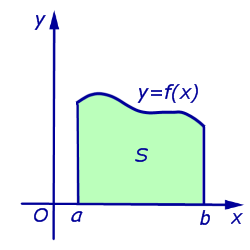
Площадь криволинейной трапеции.
Одной из основных задач, приводящих к понятию определенного интеграла, является задача о площади криволинейной трапеции, то есть фигуры (G), задаваемой на плоскости (Oxy) условиями
$$
G = ,label
$$
где (f(x)) — функция, непрерывная на отрезке ([a, b]).
Криволинейная трапеция (G) — квадрируемая фигура, площадь которой (S = S(G)) выражается формулой
$$
S = intlimits_a^b f(x) dx,label
$$
(circ) Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (M_) и (m_) — соответственно наибольшее и наименьшее значения функции (f) на отрезке (Delta_ = [x_, x_], Delta x_ = x_-x_, i = overline) (рисунок ниже).
Криволинейная трапеция
Рассмотрим клеточную фигуру (q), составленную из прямоугольников (q_ (i = overline)), таких, что длина основания (i)-го прямоугольника равна (Delta x_), а высота равна (m_).
Аналогично определяется клеточная фигура (Q), составленная из фигур (Q_), где (Q_) — прямоугольник, длина основания которого (Delta x_), а высота (M_, i = overline).
Очевидно, (q subset G subset Q), площади фигур (q) и (Q) соответственно равны
$$
S(q) = sum_^m_Delta x_,quad S(Q) = sum_^M_Delta x_.nonumber
$$
Заметим, что
$$
S(q) = s_, S(Q) = S_,label
$$
где (s_) и (S_) — соответственно нижняя и верхняя суммы Дарбу для функции (f) при разбиении (T) отрезка ([a, b]).
Так как функция (f(x)) непрерывна на отрезке ([a, b]), то в силу критерия интегрируемости для любого (varepsilon > 0) найдется такое разбиение (T) этого отрезка, что
$$
0 leq S_-s_ Замечание 3.
Ранее площадь (S) фигуры (G) была определена как предел интегральной суммы (sigma_ = displaystylesum_^f(xi_)Delta x_) при (l(T) rightarrow 0) при условии, что этот предел не зависит от разбиения (T) и выборки (xi = <xi_, i = overline>), где (xi_ in Delta_). Для непрерывной на отрезке ([a, b]) функции (displaystylelim_sigma_(xi) = intlimits_a^b f(x) dx), и поэтому оба определения площади приводят к одному и тому же результату.
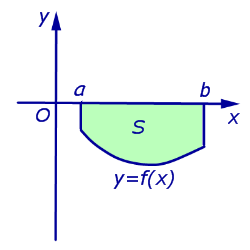
Рассмотрим теперь фигуру (D) (рис. 37.1), ограниченную отрезками прямых (x = a) и (x = b) и графиками непрерывных на отрезке ([a, b]) функций (y = f_(x)) и (y = f_(x)), где (f_(x) leq f_(x)) при (x in [a, b]). Если (f_(x) geq 0) для всех (x in [a, b]), то площадь фигуры (D) равна разности площадей криволинейных трапеций (D_) и (D_), где (D_ = <(x, y): a leq x leq b, 0 leq y leq f_(x)>, i = 1,2). Поэтому площадь фигуры (D) выражается формулой
$$
S(D) = intlimits_a^b (f_(x)-f_(x)) dx.label
$$
Формула eqref остается в силе и в случае, когда не выполняется условие (f_(x) geq 0) для всех (x in [a, b]). Чтобы убедиться в этом, достаточно сдвинуть фигуру (D) вдоль положительного направления оси (Oy) на (y_ = displaystylevertmin_f_(x)vert) и воспользоваться тем, что площади равных фигур совпадают.
Найти площадь (S) фигуры, ограниченной эллипсом
$$
frac<x^><a^> + frac<y^><b^> = 1nonumber
$$
(triangle) Искомая площадь (S) равна (4sigma), где (sigma) (рис. 37.2) — площадь криволинейной трапеции, ограниченной осями (Ox), (Oy) и графиком функции (y = b displaystylesqrt<1-frac<x^><a^>>, 0 leq x leq a). По формуле eqref находим
$$
sigma = b intlimits_0^a sqrt<1-frac<x^><a^>> dx = ab intlimits_0^1 sqrt<1-t^> dt = frac pi abnonumber
$$
(см. пример здесь). Итак, площадь, ограниченная эллипсом с полуосями (a) и (b), равна
$$
S = pi abnonumber
$$
В частности, площадь круга радиуса (R) равна (pi R^). (blacktriangle)
Отсюда следует, что площадь кругового сектора (радиуса (R)), соответствующего центральному углу (alpha), равна
$$
frac<pi R^>alpha = frac<R^alpha>.nonumber
$$
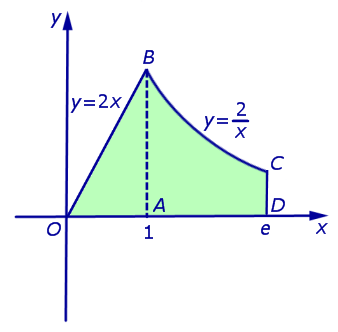
Найти площадь фигуры, ограниченной параболой (y = 6x-x^) и прямой (y = x + 4).
(triangle) Парабола (y = 6x-x^) пересекается с прямой (y = x + 4) в точках (A) и В (рис. 37.3), абсциссы которых являются корнями уравнения (6x-x^ = x + 4). Решая это уравнение, находим его корни (x_ = 1, x_ = 4). Согласно формуле eqref искомая площадь (S) равна
$$
S = intlimits_1^4 ((6x-x^)-(x + 4)) dx = left(fracx^-left.frac<x^>-4xright)right|_^ = frac. blacktrianglenonumber
$$
Рис. 37.3
Площадь криволинейного сектора.
Пусть кривая (Gamma) задана в полярной системе координат уравнением
$$
rho = rho(varphi),quad alpha leq varphi leq beta,nonumber
$$
где (rho(varphi)) — неотрицательная и непрерывная на отрезке ([alpha, beta]) функция. Тогда плоскую фигуру (G), ограниченную кривой (Gamma) и, быть может, отрезками двух лучей, составляющих с полярной осью углы (alpha) и (beta) (рис. 37.4), назовем криволинейным сектором.
Рис. 37.4
Криволинейный сектор (G) — квадрируемая фигура, площадь которой (S) выражается формулой
$$
S = frac intlimits_^ rho^(varphi) dvarphi.label
$$
(circ) Пусть (T = <varphi_, i = overline>) — разбиение отрезка ([alpha, beta]), (m_) и (M_) — соответственно наименьшее и наибольшее значения функции (rho(varphi)) на отрезке (Delta_ = [varphi_, varphi_], i = overline). Обозначим через (q_) и (Q_) круговые секторы, ограниченные лучами (varphi = varphi_, varphi = varphi_) и дугами окружностей радиусов (m_) и (M_) соответственно (рис. 37.4). Если (q) — объединение фигур (q_, ldots, q_), а (Q) — объединение фигур (Q_, ldots, Q_), то (q subset G subset Q).Так как (q_) и (Q_) — квадрируемые фигуры, то (q) и (Q) также являются квадрируемыми фигурами, а их площади соответственно равны
$$
S(q) = frac sum_^m_^Delta varphi_quad mboxquad S(Q) = frac sum_^M_^Delta varphi_.nonumber
$$
Отсюда следует, что (S(q)) и (S(Q)) совпадают соответственно с нижней и верхней суммами Дарбу для функции (displaystylefrac rho^(varphi)) на отрезке ([alpha, beta]). Поэтому (следствие из теоремы о критерии интегрируемости)
$$
sup S(q) = inf S(Q) = frac intlimits_^ rho^(varphi) dvarphi.nonumber
$$
Это означает (теорема 2), что (G) — квадрируемая фигура, а ее площадь (S) выражается формулой eqref. (bullet)
Найти площадь фигуры (G), которая ограничена лемнискатой Бернулли (рис. 37.5), заданной уравнением
$$
rho^ = a^ cos 2varphi.nonumber
$$
(triangle) Фигура (G) симметрична относительно координатных осей. Площадь (sigma) той части фигуры (G), которая лежит в первом квадранте, согласно формуле eqref равна (sigma = displaystylefrac intlimits_0^ a^ cos 2varphi dvarphi). Поэтому искомая площадь (S = 4sigma = a^). (blacktriangle)
Видео:Площадь круга через интегралСкачать

Вычисление объема тела.
Тело и его объем.
Произвольное ограниченное множество точек пространства будем называть телом.
Основные определения и утверждения, относящиеся к телам, аналогичны соответствующим определениям и утверждениям, рассмотренным выше. Поэтому некоторые утверждения для тел будут опущены.
По аналогии с понятием клеточной фигуры назовем тело клеточным, если его можно представить как объединение конечного числа непересекающихся параллелепипедов, то есть тел вида
$$
M = <(x, y, z): a_leq x leq b_, a_ leq y leq b_, a_ leq z leq b_>,nonumber
$$
а также тел, получаемых из (M) удалением части границы (или всей границы) тела (M). Объемом параллелепипеда (M) назовем число ((b_-a_)(b_-a_)(b_-a_)), а объемом клеточного тела — сумму объемов составляющих его параллелепипедов.
Тело (Omega) будем называть кубируемым, если для любого (varepsilon > 0) найдутся клеточные тела (p) и (P) такие, что
$$
p subset Omega subset P,quad 0 leq V(P)-V(p) Рис. 37.6
Если основанием цилиндрического тела (Omega) служит плоская квадрируемая фигура (G), то тело (Omega) кубируемо, а его объем (V(Omega)) равен (S(G)h), где (S(G)) — площадь основания, (h) — высота тела (Omega). В частности, объем прямого кругового цилиндра равен (V = pi R^h), где (R) — радиус основания, (h) — высота цилиндра.
(circ) По определению плоской квадрируемой фигуры для любого (varepsilon > 0) существуют такие клеточные фигуры (q) и (Q), что
$$
q subset G subset Q,quad 0 leq S(Q)-S(q) Замечание 4.
Из свойства аддитивности объема и утверждения 3 следует, что ступенчатое тело, то есть тело, являющееся объединением конечного числа цилиндрических тел, кубируемо, если основания цилиндрических тел квадрируемы; при этом объем ступенчатого тела равен сумме объемов тел, из которых составлено ступенчатое тело.
Объем тела вращения.
Тело, образованное вращением вокруг оси (Ox) криволинейной трапеции (G) (условие eqref), где (f(x)) — функция, непрерывная на отрезке ([a, b]), кубируемо, а его объем (V) выражается формулой
$$
V = pi intlimits_a^b f^(x) dx.label
$$
(circ) Пусть (T, m_, M_, Delta x_, q, Q) — те же, что и в пункте про «площадь криволинейной трапеции». При вращении вокруг оси (Ox) фигур (q), (G), (Q) получаются тела вращения (p), (Omega), (P) такие, что
$$
p subset Omega subset P,nonumber
$$
причем объемы ступенчатых тел (p) и (P) соответственно равны
$$
V(p) = pi sum_^m_^Delta x_,quad V(P) = pi sum_^M_^Delta x_.nonumber
$$
Так как (V(p)) и (V(P)) равны соответственно нижней и верхней суммам Дарбу для функции (pi f^(x)) при разбиении (T) отрезка ([a, b]), то согласно следствию из теоремы о критерии интегрируемости
$$
sup V(p) = inf V(P) = pi intlimits_a^b f^(x) dx.nonumber
$$
Следовательно, (Q) — кубируемое тело (по теореме, аналогичной теореме 2), а его объем выражается формулой eqref. (bullet)
Найти объем тела, полученного при вращении вокруг оси (Ox) фигуры, ограниченной осью (Ox) и графиком функции (y = sin x, 0 leq x leq pi).
(triangle) По формуле eqref получаем (V = pi displaystyleintlimits_0^ sin^(x) dx = frac<pi^>). (blacktriangle)
Объем тела с заданными площадями поперечных сечений.
Пусть тело (Omega) заключено между плоскостями, перпендикулярными оси Ох и пересекающими эту ось в точках (x = a) и (x = b), где (a Рис. 37.7
Обозначим через (G_) фигуру, получаемую в сечении тела (Omega) плоскостью, перпендикулярной оси (Ox) и проходящей через точку (x in [a, b]) этой оси. Будем считать, что при любом (x in [a, b]) фигура (G_) квадрируема, а ее площадь (sigma (x)) — функция, непрерывная на отрезке ([a, b]). Кроме того, предположим, что при проектировании на плоскость, перпендикулярную оси (Ox), фигур (G_) и (G_), где (alpha, beta), — любые точки отрезка ([a, b]), получаются фигуры, одна из которых содержится в другой.
При указанных выше условиях тело (Omega) кубируемо, а его объем (V) выражается формулой
$$
V = intlimits_a^b sigma(x) dx.label
$$
(circ) Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (m_) и (M_)-соответственно наименьшее и наибольшее значения функции (sigma(x)) на отрезке (Delta x_ = [x_, x_], Delta x_ = x_-x_, i = overline). Так как (sigma(x)) — непрерывная функция, то существуют точки (xi_ in Delta_) и (xi_’) такие, что (sigma(xi_) = m_, sigma(xi_’) = M_, i = overline).
Обозначим через (Omega_) ту часть тела (Omega), которая заключена между плоскостями (A_) и (A_), перпендикулярными оси (Ox) и проходящими соответственно через точки (x_) и (x_) (см. рис. 37.7).
Пусть (D_) и (D_’) — цилиндрические тела высотой (Delta x_), построенные на сечениях (G_<xi_>) и (G_<xi_’>) как на основаниях и расположенные между плоскостями (A_) и (A_). Тогда (D_ subset Omega_ subset D_’) а объемы тел (D_) и (D_’) соответственно равны
$$
V(D_) = m_Delta x_,quad V(D_’) = M_Delta x_.nonumber
$$
Если (p) — объединение тел (D_, ldots, D_), а (P) — объединение тел (D_’, ldots, D_’), то (p subset Omega subset P),
$$
V(p) = sum_^m_Delta x_,quad V(P) = sum_^M_Delta x_.nonumber
$$
Так как (sup V(p) = inf V(P) = displaystyleintlimits_a^b sigma(x) dx), то (Omega) — кубируемое тело, a его объем выражается формулой eqref. (bullet)
Вычислить объем эллипсоида (displaystylefrac<x^><a^> + frac<y^><b^> + frac<z^><c^> = 1).
(triangle) Воспользуемся тем, что площадь фигуры (G), получаемой в сечении эллипсоида плоскостью, параллельной плоскости (Oyz) и отстоящей от нее на расстоянии (x_), где (0 leq x_ leq a), равна
$$
S(x_) = pi bc (1-frac<x_^><a^>).label
$$
В самом деле, граница фигуры (G) — эллипс, задаваемый уравнениями
$$
frac<y^><b^> + frac<z^><c^> = 1-frac<x_^><a^>,quad x = x_
$$
Полуоси этого эллипса равны (blambda) и (clambda), где (lambda = displaystylesqrt<1-frac<x_^><a^>>). Используя пример 1, получаем формулу eqref, а по формуле eqref находим искомый объем эллипсоида:
$$
v = 2 intlimits_0^a S(x) dx = 2pi bc intlimits_0^a left(1-frac<x^><a^>right) dx = frac pi abc.nonumber
$$
Отсюда следует, что объем шара, радиус которого равен (R), выражается формулой (v = displaystylefrac pi R^) . (blacktriangle)
Видео:Длина дуги окружности. 9 класс.Скачать

Вычисление длины дуги кривой.
Если кривая (Gamma), заданная уравнением
$$
Gamma = <boldsymbol= boldsymbol(t), alpha leq t leq beta>,label
$$
непрерывно дифференцируема, то ее длина (S) выражается формулой
$$
S = intlimits_^ |boldsymbol'(t)| dt.label
$$
(circ) Ранее было доказано, что непрерывно дифференцируемая кривая (Gamma) спрямляема (имеет длину), а производная переменной длины дуги (s(t)) этой кривой выражается формулой
$$
s'(t) dt = |boldsymbol'(t)|.label
$$
Пусть (S) — длина всей кривой (Gamma); тогда, используя равенство eqref и формулу Ньютона-Лейбница, получаем
$$
intlimits_^ |boldsymbol'(t)| dt = intlimits_^ s'(t) dt = s(beta)-s(alpha) = S.nonumber
$$
так как (s(beta) = S), a (s(alpha) = 0). (bullet)
Если (boldsymbol(t) = (x(t), y(t), z(t))), то формула eqref принимает вид
$$
S = intlimits_^ sqrt<(x'(t))^+(y'(t))^+(z'(t))^> dt.label
$$
а если (Gamma)-плоская кривая, заданная уравнением
$$
y = f(x),quad a leq x leq b,nonumber
$$
то ее длина выражается формулой
$$
S = intlimits_a^b sqrt<1 + (f^(x))^> dx.label
$$
Найти длину кривой (y = operatorname x, 0 leq x leq a).
(triangle) Применяя формулу eqref, находим
$$
S = intlimits_0^a sqrt<1 + operatorname^x> dx = intlimits_0^a operatorname x dx = operatorname a. blacktrianglenonumber
$$
Видео:Лучший способ найти площадь кругаСкачать

Вычисление площади поверхности вращения.
Пусть (f(x)) — неотрицательная и непрерывная на отрезке ([a, b]) функция, (T = <x_, i = overline>) — разбиение отрезка ([a, b]), (L_) — ломаная с вершинами (A_(x_, f(x_)), i = overline), соединяющая последовательно точки (A_, A_, ldots A_) (рис. 37.8), (l_) — длина отрезка (mathcal_ = [A_, A_]) — (i)-го звена ломаной (L_). Тогда
$$
l_ = sqrt<(x_-x_)^ + (f(x_)-f(x_))^>.label
$$
При вращении вокруг оси (Ox) звена (mathcal_) образуется боковая поверхность усеченного конуса (цилиндра в случае, когда (f(x_) = f(x_))). Площадь этой поверхности, как известно из курса элементарной геометрии, равна
$$
p_ = pi (y_ + y_)l_,quad y_ = f(x_),quad k = overline,nonumber
$$
откуда следует, что площадь (mathcal
_) поверхности, получаемой при вращении ломаной (L_) вокруг оси (Ox), равна
$$
mathcal
_ = sum_^(y_ + y_)l_.label
$$
Если существует
$$
lim_ mathcal
_ = mathcal
.label
$$
где (l(T)) — мелкость разбиения (T), а (mathcal
_) определяется формулой eqref, то число (mathcal
) называют площадью поверхности вращения, то есть площадью поверхности, образующейся при вращении вокруг оси (Ox) графика функции (y = f(x), a leq x leq b).
Рис. 37.8
Если функция (f) имеет непрерывную производную на отрезке ([a, b]), то предел eqref существует, а площадь (mathcal
) поверхности вращения выражается формулой
$$
mathcal
= 2pi intlimits_a^b f(x) sqrt<1 + (f'(x))^> dx.label
$$
(circ) Из формул eqref и eqref следует, что
$$
mathcal
_ = pisum_^sqrt<(x_-x_)^ + (y_-y_)^>(y_ + y_),label
$$
где (y_i=f(x_i)). По теореме Лагранжа
$$
y_-y_ = f'(xi_)Delta x_,label
$$
где (xi_ in Delta_ = [x_, x_]), (Delta x_ = x_-x_). Поэтому формулу eqref можно записать в виде
$$
mathcal
_ = pi sum_^(y_ + y_) sqrt<1 + (f'(xi_))^>Delta x_.label
$$
Прибавим и вычтем в правой части равенства eqref интегральную сумму для интеграла eqref, соответствующую разбиению (T) и выборке (xi = xi_ (i = overline)), указанной формулой eqref, то есть сумму
$$
sigma_ (xi, g)= 2pi sum_^(f(xi_))sqrt<1 + (f'(xi_))^>Delta x_.label
$$
где (g(x) = 2pi f(x)displaystylesqrt<1 + (f'(x))^>). Заметим, что в силу непрерывности функции (g) для любой выборки (xi) существует
$$
lim_ sigma_ (xi, g) = 2pi intlimits_a^b f(x) sqrt<1 + (f'(x))^> dx.nonumber
$$
Поэтому для доказательства формулы eqref достаточно показать, что
$$
omega = mathcal
_-sigma_ (xi, g) rightarrow 0 mbox l(T) rightarrow 0.label
$$
Из eqref и eqref следует, что
$$
omega = pi sum_^(y_ + y_-2f(xi_i)) sqrt<1 + (f'(xi_))^>Delta x_.label
$$
При оценке величины (omega) воспользуемся тем, что функция (a) равномерно непрерывна на отрезке ([a, b]), то есть для любого (varepsilon > 0) существует (delta_ > 0) такое, что для любых точек (x’), (x″) из отрезка ([a, b]), удовлетворяющих условию (|x’-x″| 0) будет выбрано ниже.
Пусть разбиение (T) удовлетворяет условию (l(T) = displaystylemax_ Delta x_ 0) такое, что (0 0) существует (delta_ > 0) такое, что для каждого разбиения (T), мелкость (l(T)) которого удовлетворяет условию (l(T) Пример 7.
Пользуясь формулой eqref, вычислить площадь (mathcal
) поверхности сферического пояса высоты (h), если радиус сферы равен (R).
(triangle) Сферический пояс высоты (h) можно получить вращением дуги полуокружности, заданной уравнением (y = f(x) = displaystylesqrt<R^-x^>, a leq x leq b), где ([a, b] subset [-R, R], b-a = h), вокруг оси (Ox) (рис. 37.9). Так как (f'(x) =-displaystylefrac<sqrt<R^-x^>>), то (1 + (f'(x))^ = displaystylefrac<R^><R^-x^>), (f(x)sqrt<1 + (f'(x))^> = R) и по формуле eqref получаем (mathcal
_ = 2pi displaystyleintlimits_a^b R dx = 2pi R(b-a) = 2pi Rh). В частности, площадь поверхности сферы радиуса (R) равна (4pi R^). (blacktriangle)
Рис. 37.9
Видео:Как брать неберущийся интеграл Задача Найти длину дуги параболыСкачать

Применение определенного интеграла при решении физических задач.
Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; работу переменной силы; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры и так далее.
Пусть плоская пластинка (G), имеющая форму криволинейной трапеции, определяемой условиями eqref, погружена вертикально в жидкость с плотностью (rho) так, что ее боковые стороны параллельны поверхности жидкости и удалены от уровня жидкости на расстояния (a) и (b) (рис. 37.10). Требуется найти силу давления жидкости на пластинку.
Рис. 37.10
Из курса физики известно, что если пластинка погружена в жидкость и расположена горизонтально на расстоянии (h) от поверхности жидкости, то сила давления (mathcal
) на одну из сторон пластинки равна
$$
mathcal
= g rho hS,nonumber
$$
где (S) — площадь пластинки, (g) — ускорение силы тяжести. Таким образом, сила давления — линейная функция от глубины погружения пластинки. Поэтому естественно разбить пластинку (G) на части прямыми, параллельными поверхности жидкости (оси (Oy)).
Пусть (T = <x_, i = overline>) — разбиение отрезка ([a, b]). Прямыми, проведенными через точки (x_ (i = overline)), разобьем фигуру (G) на (n) частей (полосок) (G_ (i = overline)). Выделим полоску (G_), ограниченную прямыми (x = x_) и (x = x_) (рис. 37.10). Площадь этой полоски приближенно равна площади прямоугольника с основанием (Delta x_) и высотой (f(x_)), глубину погружения всех точек полоски (G_) можно считать равной (x_). Поэтому сила давления жидкости на полоску (G_) приближенно равна
$$
g rho x_f(x_)Delta x_,nonumber
$$
а сумма
$$
mathcal
_ = sum_<substack>^<substack> g rho x_f(x_)Delta x_nonumber
$$
приближенно равна силе давления жидкости на пластинку (G).
Если (l(T) rightarrow 0), где (l(T)) — мелкость разбиения (T), а функция (f) непрерывна на отрезке ([a, b]), то (mathcal
_ rightarrow mathcal
), где
$$
mathcal
= g intlimits_a^b rho x f(x) dx.label
$$
Число (mathcal
) выражаемое формулой eqref, называют силой давления жидкости на пластинку (G).
Вычислить силу давления (mathcal
) жидкости с плотностью (rho) на вертикальную стенку, имеющую форму полукруга радиуса (R) и погруженную в жидкость так, что диаметр полукруга расположен на поверхности жидкости (рис. 37.11).
Рис. 37.11
(triangle) Выберем систему координат так, как указано на рис. 37.11. Пользуясь формулой eqref, где (f(x) = sqrt<R^-x^>, a = 0, b = R), получаем
$$
mathcal
= 2g rho intlimits_0^R x sqrt<R^-x^> dx =-left.frac g rho (R^-x^)^right|_^ = frac R^. blacktrianglenonumber
$$
Видео:ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Как найти длину дуги кривой с помощью интеграла
Задачи на вычисление длины дуги кривой — однотипные. Существуют чёткие схемы для решения таких задач по формулам, которые отличаются в зависимости от того, какими и сколькими уравнениями задана кривая. Формулы представляют собой интегралы от корня, под которым в тех или иных сочетаниях присутствуют производные функций, которыми задана кривая. Следовательно, для того, чтобы вычислять длину дуги кривой, требуется уметь вычислять производные и интегралы. При вычислении интегралов возможны типичные трудности, связанные, например, с выбором подходящей подстановки. Эти задачи будем решать в примерах к данному уроку.
Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Вычисление длины дуги кривой, заданной в прямоугольных координатах
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.
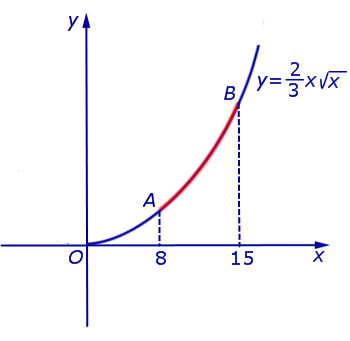
Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).
Возьмём на дуге AB точки A, M 1 , M 2 , . M i , . B с абсциссами x 0 = a, x 1 , x 2 , . x i , . b = x n и проведём хорды AM 1 , M 1 M 2 , . M n-1 B , длины которых обозначим соответственно через Δs 1 , Δs 2 , . Δs n . Тогда получим ломаную AM 1 M 2 . M n-1 B , вписанную в дугу AB. Длина ломаной равна

Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

Этот предел интегральной суммы равен определённому интегралу

Формула выше и есть формула для вычисления дуги кривой.
Пример 1. Найти длину дуги кривой 

Решение. Находим производную данной функции:
Используем формулу (1), подставляя найденную производную:
Ответ: длина дуги кривой равна 74.
Пример 2. Найти длину окружности 
Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

откуда находим производную функции:
Используем формулу (1) подставляя в неё производную, получаем:
Ответ: длина всей окружности равна 
Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

Видео:Астроида: найдем площадь и длину через определенный интегралСкачать

Вычисление длины дуги кривой, заданной параметрически
Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:
В этом случае длину дуги кривой следует находить по формуле

Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями
если 
Решение. Рассчитаем интервал, в котором будет меняться значение t, если 
Вычислим производные функций x и y:
Используем формулу (3):

Ответ: длина дуги кривой равна 26.
Если параметрическими уравнениями
задана пространственная кривая, то длина её дуги вычисляется по формуле:

Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями
Решение. Вычислим производные функций x, y и z:
Используем формулу (4):
Видео:Длина окружности и площадь кругаСкачать

Вычисление длины дуги кривой, заданной в полярных координатах
Пусть кривая задана в полярных координатах:
Длина её дуги вычисляется по формуле:

Пример 5. Найти длину дуги кривой, заданной в полярных координатах 
Решение. Вычислим производную функции:

Заданная кривая — кардиоида (рисунок выше). Так как она симметрична, вычислим только ту часть длины дуги, у которой 

🔍 Видео
Площадь круга. Математика 6 класс.Скачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

9 класс, 26 урок, Длина окружностиСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать


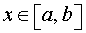 ,
,
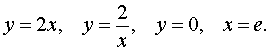
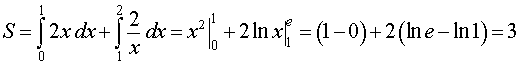
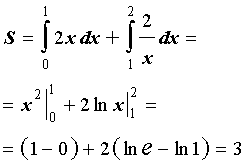
 .
.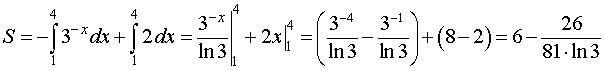
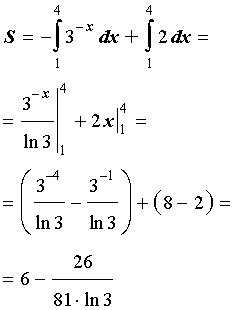
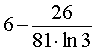 .
.
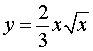 , 8 .
, 8 .