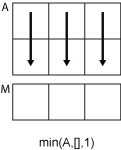
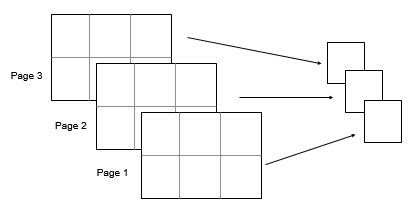
Минимальный элемент вектора матлаб (8 видео)

Нахождение максимального и минимального элементов массива

Нахождение максимального и минимального элементов массива

Самый простой анализ данных, содержащихся в некотором массиве, заключается в поиске его элементов с максимальным и минимальным значениями. В системе MATLAB определены следующие быстрые функции для нахождения минимальных и максимальных элементов массива:

mах(А) — возвращает наибольший элемент, если А — вектор; или возвращает вектор-строку, содержащую максимальные элементы каждого столбца, если А — матрица, в многомерных массивах работает с первой не единичной размерности;

mах(А.В) — возвращает массив того же размера, что А и В, каждый элемент которого есть максимальный из соответствующих элементов этих массивов;

max(A.[ ],dim) — возвращает наибольшие элементы по столбцам или по строкам матрицы в зависимости от значения скаляра dim. Например, тах(А,[ ],1) возвращает максимальные элементы каждого столбца матрицы А;

Содержание

Минимальный элемент вектора матлаб
Syntax
Description
Examples
Smallest Vector Element
Smallest Complex Element
Smallest Element in Each Matrix Column
Smallest Element in Each Matrix Row
Smallest Element Involving NaN
Smallest Element Indices
Minimum of Array Page
Return Linear Indices
Smallest Element Comparison
Input Arguments
A — Input array scalar | vector | matrix | multidimensional array
dim — Dimension to operate along positive integer scalar
vecdim — Vector of dimensions vector of positive integers
B — Additional input array scalar | vector | matrix | multidimensional array
Минимальный элемент вектора матлаб
📺 Видео

Видео:Язык C++ с нуля | #33 Найти максимальный и минимальный элемент массива в c++Скачать

Минимальный элемент вектора матлаб

Minimum elements of an array

Видео:MATLAB 04 Массивы и матрицыСкачать

Syntax

Видео:Найти минимальный элемент массива. Поиск минимального элемента в массиве. C++ для начинающих. ДЗ#8.Скачать

Description

M = min( A ) returns the minimum elements of an array.

If A is a vector, then min(A) returns the minimum of A .

If A is a matrix, then min(A) is a row vector containing the minimum value of each column.

If A is a multidimensional array, then min(A) operates along the first array dimension whose size does not equal 1 , treating the elements as vectors. The size of this dimension becomes 1 while the sizes of all other dimensions remain the same. If A is an empty array with first dimension 0 , then min(A) returns an empty array with the same size as A .

M = min( A ,[], dim ) returns the minimum element along dimension dim . For example, if A is a matrix, then min(A,[],2) is a column vector containing the minimum value of each row.

M = min( A ,[], nanflag ) specifies whether to include or omit NaN values in the calculation. For example, min(A,[],’includenan’) includes all NaN values in A while min(A,[],’omitnan’) ignores them.

M = min( A ,[], dim , nanflag ) also specifies the dimension to operate along when using the nanflag option.

[ M , I ] = min( ___ ) also returns the index into the operating dimension that corresponds to the minimum value of A for any of the previous syntaxes.

M = min( A ,[], ‘all’ ) finds the minimum over all elements of A . This syntax is valid for MATLAB ® versions R2018b and later.

M = min( A ,[], vecdim ) computes the minimum over the dimensions specified in the vector vecdim . For example, if A is a matrix, then min(A,[],[1 2]) computes the minimum over all elements in A , since every element of a matrix is contained in the array slice defined by dimensions 1 and 2.

M = min( A ,[], ‘all’ , nanflag ) computes the minimum over all elements of A when using the nanflag option.

M = min( A ,[], vecdim , nanflag ) specifies multiple dimensions to operate along when using the nanflag option.

[ M , I ] = min( A ,[], ‘all’ , ___ ) returns the linear index into A that corresponds to the minimum value in A when specifying ‘all’ .

[ M , I ] = min( A ,[], ___ ,’linear’) returns the linear index into A that corresponds to the minimum value in A .

C = min( A , B ) returns an array with the smallest elements taken from A or B .

C = min( A , B , nanflag ) also specifies how to treat NaN values.

___ = min( ___ ,’ComparisonMethod’, method ) optionally specifies how to compare elements for any of the previous syntaxes. For example, for a vector A = [-1 2 -9] , the syntax min(A,[],’ComparisonMethod’,’abs’) compares the elements of A according to their absolute values and returns -1 .

Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Examples

Smallest Vector Element

Create a vector and compute its smallest element.

Smallest Complex Element

Create a complex vector and compute its smallest element, that is, the element with the smallest magnitude.

Smallest Element in Each Matrix Column

Create a matrix and compute the smallest element in each column.

Smallest Element in Each Matrix Row

Create a matrix and compute the smallest element in each row.

Smallest Element Involving NaN

Create a vector and compute its minimum, excluding NaN values.

min(A) will also produce this result since ‘omitnan’ is the default option.

Use the ‘includenan’ flag to return NaN .

Smallest Element Indices

Create a matrix A and compute the smallest elements in each column as well as the row indices of A in which they appear.

Minimum of Array Page

Create a 3-D array and compute the minimum over each page of data (rows and columns).

Starting in R2018b, to compute the minimum over all dimensions of an array, you can either specify each dimension in the vector dimension argument, or use the ‘all’ option.

Return Linear Indices

Create a matrix A and return the minimum value of each row in the matrix M . Use the ‘linear’ option to also return the linear indices I such that M = A(I) .

Smallest Element Comparison

Create a matrix and return the smallest value between each of its elements compared to a scalar.

Видео:Matlab Tutorial - 28 - Creating Vectors with Evenly Spaced ElementsСкачать

Input Arguments

A — Input array
scalar | vector | matrix | multidimensional array

Input array, specified as a scalar, vector, matrix, or multidimensional array.

If A is complex, then min(A) returns the complex number with the smallest magnitude. If magnitudes are equal, then min(A) returns the value with the smallest magnitude and the smallest phase angle.

If A is a scalar, then min(A) returns A .

If A is a 0-by-0 empty array, then min(A) is as well.

If A has type categorical , then it must be ordinal.

dim — Dimension to operate along
positive integer scalar

Dimension to operate along, specified as a positive integer scalar. If no value is specified, then the default is the first array dimension whose size does not equal 1.

Dimension dim indicates the dimension whose length reduces to 1 . The size(M,dim) is 1 , while the sizes of all other dimensions remain the same, unless size(A,dim) is 0 . If size(A,dim) is 0 , then min(A,dim) returns an empty array with the same size as A .

Consider a two-dimensional input array, A :

If dim = 1 , then min(A,[],1) returns a row vector containing the smallest element in each column.

If dim = 2 , then min(A,[],2) returns a column vector containing the smallest element in each row.

min returns A if dim is greater than ndims(A) .

vecdim — Vector of dimensions
vector of positive integers

Vector of dimensions, specified as a vector of positive integers. Each element represents a dimension of the input array. The lengths of the output in the specified operating dimensions are 1, while the others remain the same.

Consider a 2-by-3-by-3 input array, A . Then min(A,[],[1 2]) returns a 1-by-1-by-3 array whose elements are the minimums computed over each page of A .

B — Additional input array
scalar | vector | matrix | multidimensional array

Additional input array, specified as a scalar, vector, matrix, or multidimensional array. Inputs A and B must either be the same size or have sizes that are compatible (for example, A is an M -by- N matrix and B is a scalar or 1 -by- N row vector). For more information, see Compatible Array Sizes for Basic Operations.

A and B must be the same data type unless one is a double . In that case, the data type of the other array can be single , duration , or any integer type.

If A and B are ordinal categorical arrays, they must have the same sets of categories with the same order.

Видео:Matlab создание вектора данныхСкачать

Минимальный элемент вектора матлаб

В системе MatLab достаточно просто выполняются математические операции над матрицами и векторами. Рассмотрим сначала простые операции сложения и умножения матриц и векторов. Пусть даны два вектора

a = [1 2 3 4 5]; % вектор-строка
b = [1; 1; 1; 1; 1]; % вектор-столбец

тогда умножение этих двух векторов можно записать так

c = a*b; % c=1+2+3+4+5=16
d = b*a; % d – матрица 5х5 элементов

В соответствии с операциями над векторами, умножение вектор-строки на вектор-столбец дает число, а умножение вектор-столбца на вектор-строку дает двумерную матрицу, что и является результатом вычислений в приведенном примере, т.е.

Сложение и вычитание двух векторов записывается так

a1 = [1 2 3 4 5];
a2 = [5 4 3 2 1];
c = a1+a2; % c = [1+5, 2+4, 3+3, 4+2, 5+1];
с = a2-a1; % c = [5-1, 4-2, 3-3, 2-4, 1-5];

Следует обратить внимание, что операции сложения и вычитания можно выполнять между двумя векторами-столбцами или двумя векторами-строками. Иначе MatLab выдаст сообщение об ошибке, т.к. разнотипные векторы складывать нельзя. Так обстоит дело со всеми недопустимыми арифметическими операциями: в случае невозможности их вычисления система MatLab сообщит об ошибке и выполнение программы будет завершено на соответствующей строке.

Аналогичным образом выполняются операции умножения и сложения между матрицами:

A = [1 2 3; 4 5 6; 7 8 9];
B = ones(3);
C = A+B; % сложение двух матриц одинакового размера
D = A+5; % сложение матрицы и числа
E = A*B; % умножение матрицы А на В
F = B*A; % умножение матрицы В на А
G = 5*A; % умножение матрицы на число

Операции вычисления обратной матрицы, а также транспонирования матриц и векторов, записываются следующим образом:

a = [1 1 1]; % вектор-строка
b = a’; % вектор-столбец, образованный
% транспонированием вектора-строки а.
A = [1 2 3; 4 5 6; 7 8 9]; % матрица 3х3 элемента
B = a*A; % B = [12 15 18] – вектор-строка
C = A*b; % C = [6; 15; 24] – вектор-столбец
D = a*A*a’; % D = 45 – число, сумма эл-ов матрицы А
E = A’; % E – транспонированная матрица А
F = inv(A); % F – обратная матрица А
G = A^-1; % G – обратная матрица А

Из приведенного примера видно, что операция транспонирования матриц и векторов обозначается символом ‘ (апостроф), который ставится после имени вектора или матрицы. Вычисление обратной матрицы можно делать путем вызова функции inv() или возводя матрицу в степень -1. Результат в обоих случаях будет одинаковым, а два способа вычисления сделано для удобства использования при реализации различных алгоритмов.

Если в процессе вычислений требуется поэлементно умножить, разделить или возвести в степень элементы вектора или матрицы, то для этого используются операторы:

.* — поэлементное умножение;
./ и . — поэлементные деления;
.^ — поэлементное возведение в степень.

Рассмотрим работу данных операторов на следующем примере.

a = [1 2 3]; % вектор-строка
b = [3 2 1]; % вектор-строка
c = a.*b; % c = [3 4 3]
A = ones(3); % матрица 3х3, состоящая из единиц
B = [1 2 3;4 5 6; 7 8 9]; % матрица 3х3
C = A.*B; % матрица 3х3, состоящая из
D = A./B; % матрица 3х3, состоящая из
E = A.B; % матрица 3х3, состоящая из
F = A.^2; % возведение элементов матрицы А в квадрат

В заключении данного параграфа рассмотрим несколько функций полезных при работе с векторами и матрицами.

Для поиска максимального значения элемента вектора используется стандартная функция max(), которая возвращает найденное максимальное значение элемента и его позицию (индекс):

a = [1 6 3 4];
[v, i] = max(a); % v = 6, i = 2;

Приведенный пример показывает два разных способа вызова функции max(). В первом случае определяется и максимальное значение элемента и его индекс в векторе, а во втором – только максимальное значение элемента.

В случае с матрицами, данная функция определяет максимальные значения, стоящие в столбцах, как показано ниже в примере:

A = [4 3 5; 6 7 2; 3 1 8];
[V, I] = max(A); % V=[6 7 8], I = [2 2 3]
V = max(A); % V=[6 7 8]

Полный синтаксис функции max() можно узнать, набрав в командном окне MatLab команду

Аналогичным образом работает функция min(), которая определяет минимальное значение элемента вектора или матрицы и его индекс.

Другой полезной функцией работы с матрицами и векторами является функция sum(), которая вычисляет сумму значений элементов вектора или столбцов матрицы:

a = [3 5 4 2 1];
s = sum(a); % s = 3+5+4+2+1=15
A = [4 3 5; 6 7 2; 3 1 8];
S1 = sum(A); % S1=[13 11 15]
S2 = sum(sum(A)); % S2=39

При вычислении суммы S2 сначала вычисляется сумма значений элементов матрицы А по столбцам, а затем, по строкам. В результате, переменная S2 содержит сумму значений всех элементов матрицы А.

Для сортировки значений элементов вектора или матрицы по возрастанию или убыванию используется функция sort() следующим образом:

b1 = sort(a); % b1=[1 2 3 4 5]
b2 = sort(a, ‘descend’); % b2=[5 4 3 2 1]
b3 = sort(a, ‘ascend’); % b3=[1 2 3 4 5]

A = [4 3 5; 6 7 2; 3 1 8];
B1 = sort(A); % B1=[3 1 2
% 4 3 5
% 6 7 8]
B2 = sort(A, ‘descend’); % B2=[6 7 8
% 4 3 5
% 3 1 2]

Во многих практических задачах часто требуется найти определенный элемент в векторе или матрице. Это можно выполнить с помощью стандартной функции find(), которая в качестве аргумента принимает условие, в соответствии с которым и находятся требуемые элементы, например:

a = [3 5 4 2 1];
b1 = find(a == 2); % b1 = 4 – индекс элемента 2
b2 = find(a

= 2); % b2 = [1 2 3 5] – индексы без 2
b3 = find(a > 3); % b3 = [2 3]

В приведенном примере символ ‘==’ означает проверку на равенство, а символ ‘

=’ выполняет проверку на неравенство значений элементов вектора а. Более подробно об этих операторах будет описано в разделе условные операторы.

Еще одной полезной функцией работы с векторами и матрицами является функция mean() для вычисления среднего арифметического значения, которая работает следующим образом:

a = [3 5 4 2 1];
m = mean(a); % m = 3
A = [4 3 5; 6 7 2; 3 1 8];
M1 = mean(A); % M1 = [4.333 3.667 5.000]
M2 = mean(mean(A)); % M2 = 4.333

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт