Дивергенция вектора в цилиндрических координатах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Дифференциальные уравнения векторных линий Рассмотрим поле вектора Уравнения векторных линий в криволинейных координатах q, q2i g3 имеют вид В цилиндрических координатах в сферических координатах 14.2. Градиент в ортогональных координатах Пусть скалярное поле. Тогда Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах В цилиндрических координатах в сферических координатах 14.3. Ротор в ортогональных координатах Рассмотрим векгорное поле и вычислим rot а. Имеем В цилиндрических координатах в сферических координатах 14.4. Дивергенция в ортогональных координатах Дивергенция div а векторного поля вычисляется по формуле.

В цилиндрических координатах или в сферических координатах

Применяя формулу (7) к единичным векторам получим Вычисление потока в криволинейных координатах Пусть S — часть координатной поверхности , ограниченная координатными линиями Тогда поток вектора через поверхность 5 в направлении вектора ei вычисляется по формуле Аналогично вычисляется поток через часть поверхности д2 = с, а также через часть поверхности д3 = с, где с = const. Пример I.

Найти поток П векторного поля через внешнюю сторону верхней полусферы 5 радиуса R с центром в начале координат. Ч Полусфера S есть часть юординатной поверхности г = const, а именно г = R. На полусфере 5 имеем , причем Учитывая, что в сферических коорои патах по формуле (8) найдем 14.6. Вычисление потенциала в криволинейных координатах Пусть в некоторой области О задано потенциальное векторное поле в области Для нахождения потенциала ) этого векторного поля запишем равенство в следующем виде:

Отсюда следует, что Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал произвольная постоянная. В цилиндрических координатах система (9) принимает вид В сферических координатах система (9) имеет вид Пример 2. Найти потенциал векторного поля, заданного в цилиндрических координа тех Убедимся, что По формуле (5) л о лучим данное поле потенциально.

Искомый потенциал и = и(р, у, г) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)): Интегрированием по р из первого уравнения находим Дифференцируя соотношение (11) no р и используя второе уравнение, получим или откуда . Таким образом.

Возможно вам будут полезны данные страницы:

Дифференцируя это соотношение no z и используя тре тье уравнение, получим Линейный интеграл и циркуляция в ортогональных криволинейных координатах Пусть векторное поле определено и непрерывно в области Q изменения ортогональных криволинейных координат 4i, 42, 4з • Так как дифференциал радиус-вектора г любой точки M(qb 42, 43) G П выражается формулой то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L СП будет равен В частности, для цилиндрических координат ) будем иметь.

Отсюда по формуле (13) получим Аналогично для сферических координат будем иметь Отсюда по формуле (13) получим Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах.

Оператор Лапласа в ортогональных координатах Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а(М) в криволинейных координатах 4,, q2, 43 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно. Пример 3. Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах по замкнутой кривой L, Координаты данного вектора равны соответственно Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).

Подставляя координаты данного вектора в формулу.(14), получим На кривой L имеем . Искомая циркуляция будет равна 14.8. Оператор Лапласа в ортогональных координатах Если скалярная функция, то Используя формулы (16) и (17), для оператора Лапласа Д получим следующее выражение В цилиндрических координатах получим В сферических координатах будем иметь Пример 4. Найти все решения уравнения Лапласа Аи = 0, зависящие только от расстояния г.

Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т., то уравнение Лапласа Ди = 0 в сферических координатах будет иметь вид Отсюда так что где постоянные. Упражнения Найдите производную скалярного поля в точке по направлению кточке Найдите производную скалярного поля и(х, у, z) в точке Л#о(хо, Уо» *о) по направлению нормали к поверхности S, образующей острый угол с положительным направлением оси О г: 6.

Найдите производную скалярного поля в точке эллипса + = 1 по направлению внешней нормали к эллипсу в этой точке. 7. Найдите производную скалярного поля в точке по направлению окружности 8. Найдигеугол между градиентами функции и = arctg | в точках 9. Найдите производную плоского поля и вточке понаправле-нию, задаваемому вектором, лежащим в плоскости хОу и наклоненным под углом | коси Ох. Найдите векторные линии следующих векторных полей: 13.

через точку 14. Найдите векгорную линию поля а, проходящую через точку М(3,4, -1). 15. Вычислите поток векторного поля через верхнюю сторону круга, вырезаемого конусом х2 4- у2 = г2 из плоскости 16. Вычислите поток векторного поля к через треугольник ABC с вершинами в точках (нормаль образует с осью Oz острый угол). 17. Вычислите поток векторного поля а = xi + zk через боковую поверхность кругового цилиндра , ограниченную плоскостями z 18.

Вычислите поток векторного поля а = yzi — xj — yk через полную поверхность конуса х2 + у2 = z2, ограниченную плоскостью z Методом введения криволинейных координат на поверхности вычислите поток заданного векгора а через заданную поверхность S: 19. — внешняя сторона цилиндрической поверхности х2 + у2 = 9, ограниченной сферой Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах.

Дивергенция в ортогональных координатах

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах 20. — внешняя сторона части сферы , вырезанная конической поверхностью Вычислите поток векгорного поля а через замкнутую поверхность S (нормаль внешняя). Проверьте результат с помощью формулы Гаусса—Остроградского:

Достраивая подходящим образом заданные незамкнутые поверхности до замкнутых и пользуясь теоремой Гаусса—Остроградского, вычислите потоки векторных полей через указанные поверхности (к замкнутой поверхности берем внешнюю нормаль): Найдите работу силы F при перемещении вдольлинии L от точки М к точке N: Найдите циркуляцию векторного поля а вдоль замкнутого контура L (в направлении, соответствующем возрастанию параметра Вычислите циркуляцию векторного поля а по замкнутому контуру L.

Проверьте результат при помощи формулы Стокса: — линия пересечения плоскости с координатными плоскостями 38. Найдите дивергенцию векторного пол я а = (с, г), где с — постоянный вектор, . 39. При какой функции ip(z) дивергенция векгорного поля а =)k будет равна z? 40. Найдите , где г = 41. Найдите функцию tf>(r), для которой выполняется равенство 42. Какова должна быть функция /(х, z), чтобы ротор векгорного поля совпал с вектором Найдите ротор следующих векторов: Докажите, что следующие векторные поля являются потенциальными, и найдите их потенциалы: Ответы

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Оператор Лапласа в криволинейных координатахСкачать

Дивергенция

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Дивергенция

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

У этого термина существуют и другие значения, см. Дивергенция (биология).

Дивергенция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток).

Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учетом знака. Поэтому можно дать более короткое определение дивергенции:

дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Оператор дивергенции, применённый к полю , обозначают как

.

Видео:Демидович №4433: дивергенция в полярных координатахСкачать

Содержание

1 Определение 2 Определение в декартовых координатах 3 Физическая интерпретация 4 Свойства 5 Дивергенция в ортогональных криволинейных координатах
5.1 Цилиндрические координаты 5.2 Сферические координаты 5.3 Параболические координаты 5.4 Эллиптические координаты

6 Дивергенция в произвольных криволинейных координатах и её обобщение

6.1 Свойства дивергенции тензора

7 См. также

Видео:Демидович №4434: дивергенция в криволинейной системеСкачать

// [править] Определение

Определение дивергенции выглядит так:

где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объем V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю. Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат, приведённые в следующем параграфе).

Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

[править] Определение в декартовых координатах

Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением

Это же выражение можно записать с использованием оператора набла

Многомерная, а также двумерная и одномерная, дивергенция определяется в декартовых координатах в пространствах соответствующей размерности совершенно аналогично (в верхней формуле меняется лишь количество слагаемых, а нижняя остается той же, подразумевая оператор набла подходящей размерности).

Видео:§55 Цилиндрическая система координатСкачать

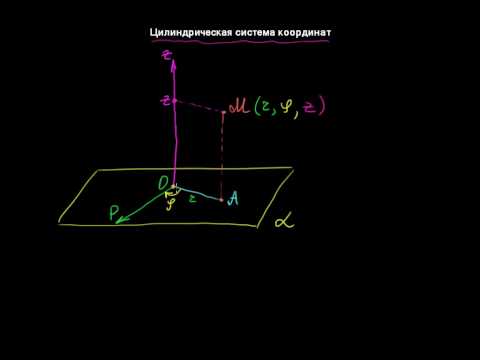
[править] Физическая интерпретация

С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля:

0 » width=»80″ height=»14 src=»/> — точка поля является источником;

— точка поля является стоком;

— стоков и источников нет, либо они компенсируют друг друга.

Например, если в качестве векторного поля взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся).

Ещё одним, быть может, несколько схематическим, примером может служить озеро (для простоты — постоянной единичной глубины со всюду горизонтальной скоростью течения воды, не зависящей от глубины, давая, таким образом двумерное векторное поле на двумерном пространстве). Если угодно иметь более реалистическую картину, то можно рассмотреть горизонтальную проекцию скорости, проинтегрированную по вертикальной пространственной координате, что даст ту же картину двумерного векторного поля на двумерном пространстве, причём картина качественно будет для наших целей не сильно отличаться от упрощённой первой, количественно же являться её обобщением (весьма реалистическим). В такой модели (и в первом, и во втором варианте) родники, бьющие из дна озера будут давать положительную дивергенцию поля скоростей течения, а подводные стоки (пещеры, куда вода утекает) — отрицательную дивергенцию.

Дивергенция вектора плотности тока дает минус скорость накопления заряда в обычной трёхмерной физике (так как заряд сохраняется, то есть не исчезает и не появляется, а может только переместиться через границы какого-то объёма, чтобы накопиться в нем или уйти из него; а если и возникают или исчезают где-то положительные и отрицательные заряды — то только в равных количествах). (См. Уравнение непрерывности).

Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

[править] Свойства

Следующие свойства могут быть получены из обычных правил дифференцирования.

Линейность: для любых векторных полей F и G и для всех действительных чисел a и b

Если φ — скалярное поле, а F — векторное, тогда:

или

Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:

или

Дивергенция от градиента есть лапласиан:

Дивергенция от ротора:

Видео:Демидович №4415.1а: градиент в цилиндрических координатахСкачать

[править] Дивергенция в ортогональных криволинейных координатах

, где Hi — коэффициенты Ламе.

[править] Цилиндрические координаты

.

[править] Сферические координаты

.

[править] Параболические координаты

.

[править] Эллиптические координаты

.

Видео:ДивергенцияСкачать

[править] Дивергенция в произвольных криволинейных координатах и её обобщение

Формулу для дивергенции векторного поля в произвольных координатах (в любой конечной размерности) нетрудно получить из общего определения через предел отношения потока к объёму, воспользовавшись тензорной записью смешанного произведения и тензорной формулой объёма.

Существует обобщение операции дивергенции на действие не только на векторы, но и на тензоры более высокого ранга.

В общем случае дивергенция определяется через ковариантной производной:

, где — координатные векторы.

Это позволяет находить выражения для дивергенции в произвольных координатах для векторного:

.

или тензорного поля:

.

В общем случае, дивергенция понижает ранг тензора на 1.

📽️ Видео

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Демидович №4440.1: ротор в полярных координатахСкачать

Дивергенция векторного поляСкачать

Цилиндрическая система координат(ЦСК).Тройной интегралСкачать

Цилиндрические координатыСкачать

Демидович №4442: поток вектора через цилиндрСкачать

Оператор Лапласа в полярных координатахСкачать

ДивергенцияСкачать

Полярная система координатСкачать

Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Скорость и ускорение точки в полярных координатахСкачать