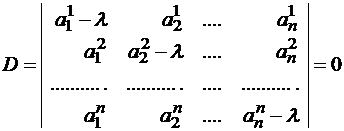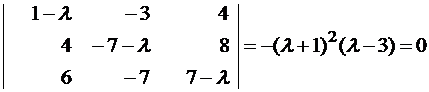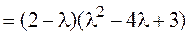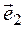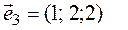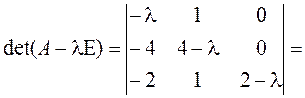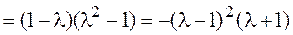Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 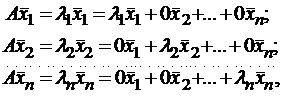

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
- Правило отыскания собственных чисел и собственных векторов
- Свойства собственных векторов
- Приведение квадратной матрицы к диагональному виду
- Упражнения
- Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду
- Страницы работы
- Фрагмент текста работы
- 🔥 Видео
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 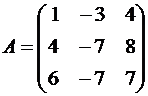
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Свойства собственных векторов
Для любого собственного значения Хк(А) существует п- кг линейно независимых собственных векторов
образующих фундаментальную систему решений однородной системы уравнений (А — ХкЕ)Х = 0. Здесь гк = г(А — ХкЕ) — ранг матрицы А — ХкЕ.
Множество всех собственных векторов А(Хк), соответствующих собственному значению Хк <А)матрицы Л, совпадает с общим решением однородной системы уравнений (Л — ХкЕ)Х = ©, т. е.
Любые два собственных вектора F <XJи F(X2), соответствующие различным собственным значениям А, ф А2 характеристического уравнения А — ХЕI = 0 матрицы А, являются линейно независимыми.
Если F(A,j), F(Х2) линейно независимые, то равенство F(X<)a + + Е(А9)Р = 0 выполняется только при а = Р = 0. Предположим, что F(Xl)а + Е(А9)Р = 0 при р * 0. Так как F(Xl) и F(X2) — собственные векторы, то они удовлетворяют уравнению АХ = XX, т. е.
Умножим первое равенство на а, второе на Р и сложим, получим
По предположению F(Xx)a + Е(А9)р = 0, тогда 
Так как по условию X,, * Xv а по предположению р * 0, то F(X2) = 0. Это противоречит тому, что собственным вектором может быть только ненулевой вектор.
Система собственных векторов, составленная из систем собственных векторов, соответствующих различным собственным значениям АДА!), А2(Л). АП(Л), является линейно независимой.
Пример 7.1. Найти собственные значения и собственные векторы матрицы
Решение. Составим систему (А — ХЕ)Х = 0, которая в координатной записи имеет вид
Приравняем определитель матрицы этой системы к нулю
Раскроем этот определитель по правилу треугольника, получим характеристическое уравнение
Найдем характеристические значения матрицы А (корни этого уравнения):
Для каждого из характеристических значений найдем собственные векторы.
При = 1 система (7.1) принимает вид
Система является разрешенной. Включим в набор разрешенных неизвестных х< и хт Свободной неизвестной х3 придадим значение д’3 = 1, получим решение С(Х1) = (1, 0, -1), которое является собственным вектором.
Аналогично найдем соответствующие собственным значениям Х2 и Х3 собственные векторы
Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Приведение квадратной матрицы к диагональному виду
Матрицу А можно привести к диагональному виду с помощью матрицы Г, если матрица Т
г АТявляется диагональной.
Для нахождения матрицы Т необходимо найти собственные значения и собственные векторы матрицы А. Матрицу Т составляют из собственных векторов-столбцов. Если эта матрица является квадратной, то матрицу А можно привести к диагональному виду.
Пример 7.2. Матрицу
привести к диагональному виду.
Решение. В предыдущем примере для матрицы А были найдены собственные значения
и соответствующие им собственные векторы 
Найдем обратную матрицу Т 1 с использованием присоединенной матрицы.
Найдем произведение матриц Т 1 АТ:
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Упражнения
7.1. Найти собственные значения и собственные векторы матрицы А. Записать матрицу Т приводящую матрицу А к диагональному виду и Гр
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду
Страницы работы
Фрагмент текста работы
§ 2. Приведение квадратной матрицы к диагональному виду
Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица 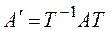
Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица 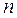
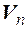
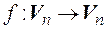
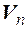
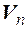
2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни 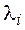
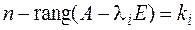
где 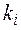
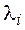
При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.
В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице 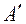
Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:
1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;
2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;
3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу 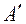
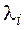
4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;
5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей 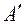
Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если
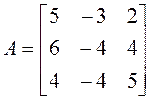
►Проводим решение по намеченному плану.

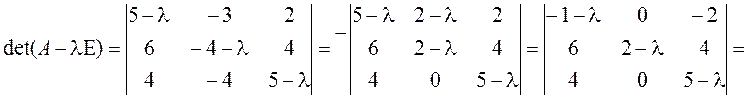
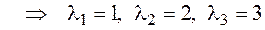
2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.
3. 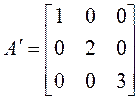
4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.
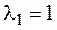
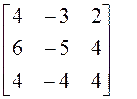
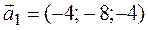
(алгебраические дополнения к элементам первой строки);
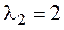
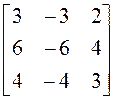
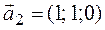
(алгебраические дополнения к элементам второй строки);
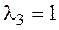
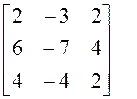
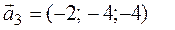
(алгебраические дополнения к элементам первой строки).
5. Составляем матрицу 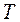
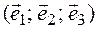
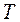
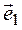
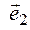
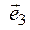
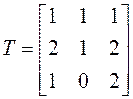
Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
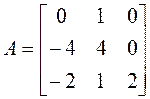
►Составляем и решаем характеристическое уравнение:
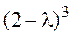
Матрица имеет только одно собственное значение 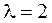
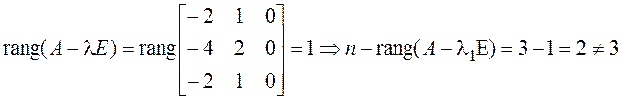
Условие не выполняется, значит, матрица к диагональному виду не приводится.◄
Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
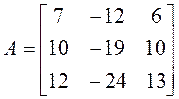
► Решение опять проводим по намеченному плану.

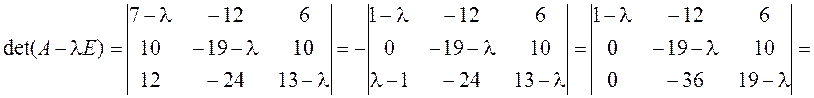
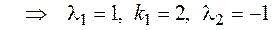
2. Проверяем выполнение условия (7) для кратного корня:
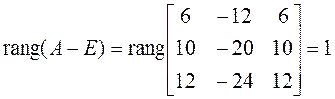
Таким образом, 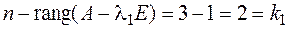
3. 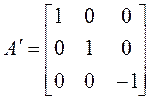
4. Так как 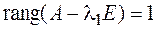
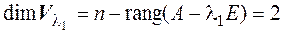
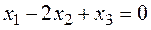
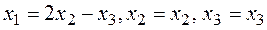
🔥 Видео
Собственные значения и собственные векторыСкачать

Собственные векторы и собственные значения матрицыСкачать

Диагональная матрица линейного оператораСкачать

Диагонализация матрицы линейного оператора. ПримерСкачать

Линал 4.3 Диагонализация матрицыСкачать

7 4 Собственные векторы и собственные значенияСкачать

Диагонализация матрицы линейного оператора. ТемаСкачать

Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

14.1 Собственные значения и собственные векторы линейного оператора.Скачать

Линал 1.8 Собственные векторы и собственные числаСкачать

Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Собственные значения и собственные векторы. ТемаСкачать

Собственные значения и собственные векторы. ПримерСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать