Диагональ четырехугольника делит его на два равновеликих

О чем эта статья:

Определение параллелограмма

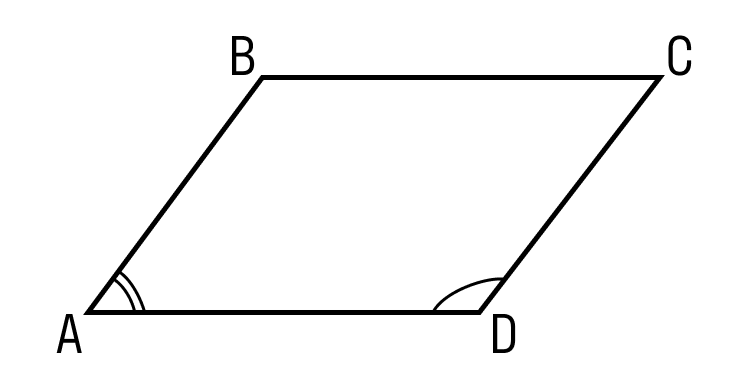
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

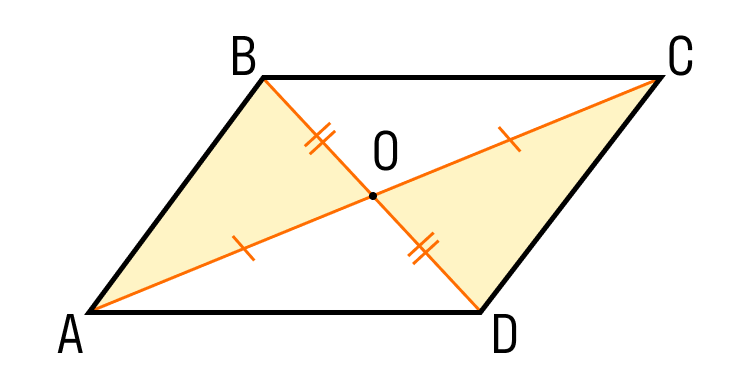
1. В параллелограмме точка пересечения диагоналей делит их пополам.
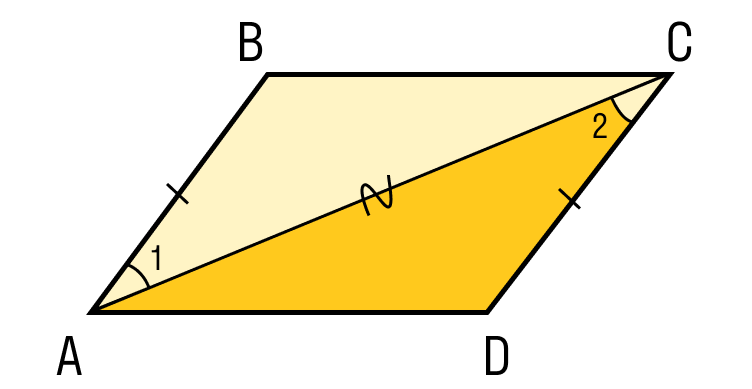
2. Любая диагональ параллелограмма делит его на два равных треугольника.
3. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.

Как найти площадь параллелограмма:

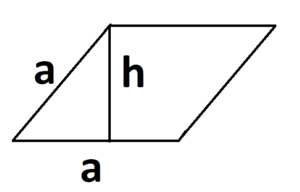
1. S = a × h, где a — сторона, h — высота.
   
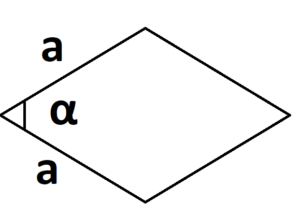
2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
   
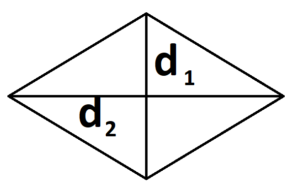
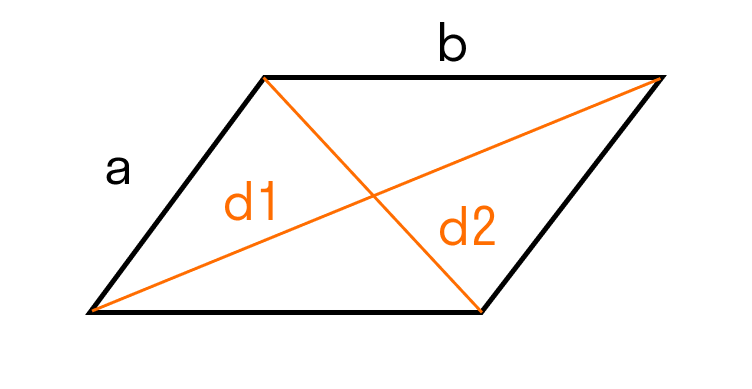
3. Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
   Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
   

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

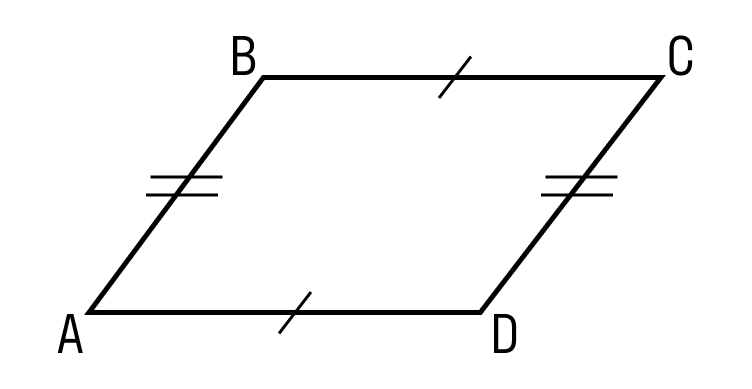
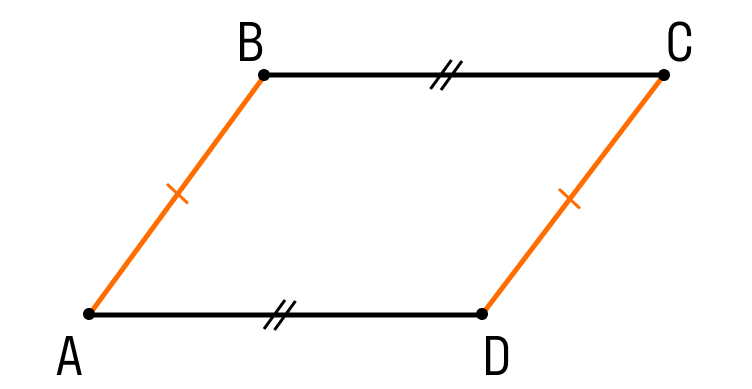
1. Противоположные стороны параллелограмма равны.
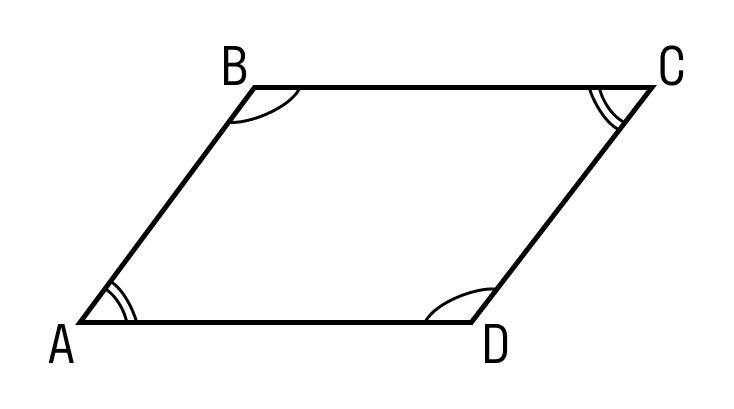
   ABCD — параллелограмм, значит, AB = DC, BC = AD.
   
2. Противоположные углы параллелограмма равны.
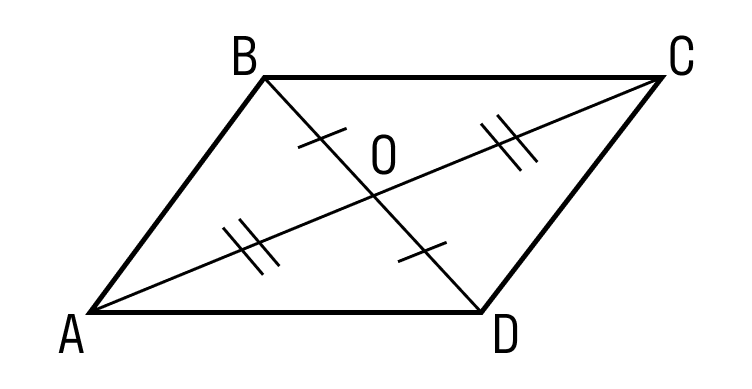
   ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
   
3. Диагонали параллелограмма точкой пересечения делятся пополам.
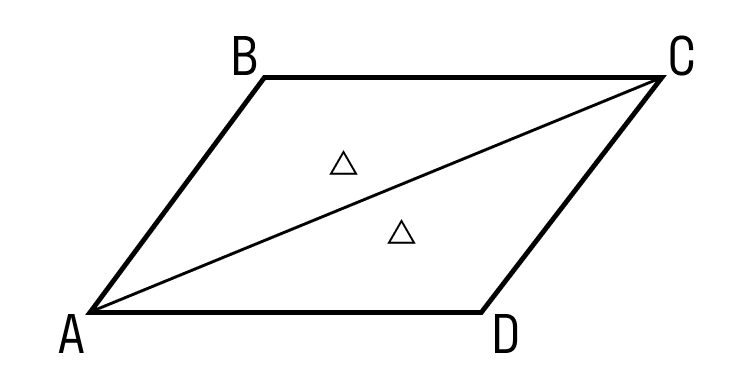
   ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
   
4. Диагональ делит параллелограмм на два равных треугольника.
   ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
   
5. Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
   ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
   
6. В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
   

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

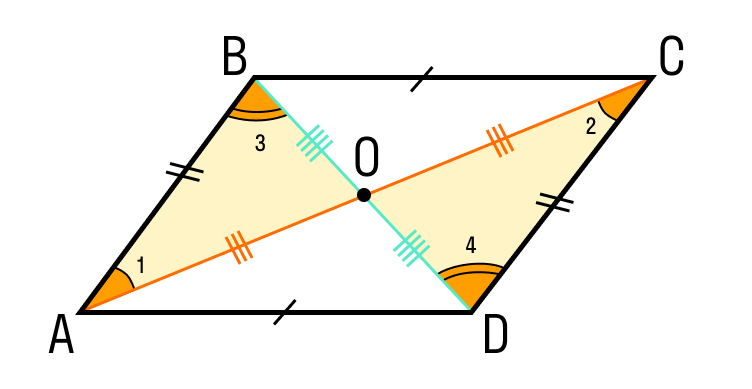
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

1. AB = CD как противоположные стороны параллелограмма.
2. ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
3. Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
   • CO = AO
   • BO = DO

   

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

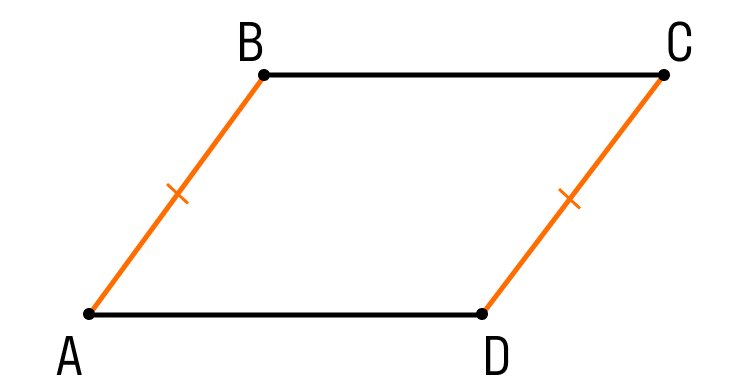
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB || CD
• AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

1. AC — общая сторона;
2. По условию AB = CD;
3. ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB = CD
• BC = AD

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

• AC — общая сторона;
• AB = CD по условию;
• BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

• CO = OA;
• DO = BO;
• углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Параллелограммы

Свойства и признаки параллелограмма

Свойства и признаки прямоугольника

Свойства и признаки ромба

Свойства и признаки квадрата

Свойства и признаки параллелограмма

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Параллелограмм		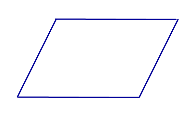Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Определение	Диагонали параллелограмма		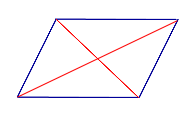Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Определение	Высота параллелограмма		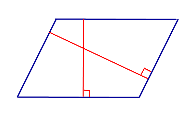Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Свойство	Равенство противолежащих сторон		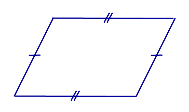Если четырёхугольник является параллелограммом, то его противолежащие стороны равны
Признак			Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом
Признак	Равенство и параллельность двух противолежащих сторон		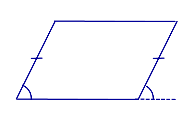Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом
Свойство	Диагонали точкой пересечения делятся пополам		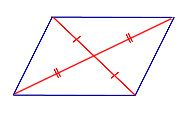Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам
Признак			Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом
Свойство	Суммы углов, прилежащих к сторонам		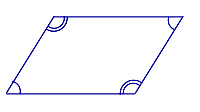Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°
Признак			Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180° , то четырёхугольник является параллелограммом
Свойство	Равенство противолежащих углов		Если четырёхугольник является параллелограммом, то его противолежащие углы равны
Признак			Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом
Свойство	Два треугольника, на которые каждая диагональ делит четырёхугольник		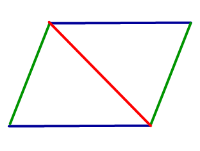Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника
Признак			Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом
Свойство	Четыре треугольника, на которые диагонали делят четырёхугольник		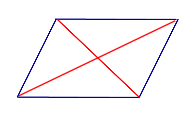Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак			Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом

Определение: параллелограмм
	Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Определение: диагонали параллелограмма
	Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Определение: высота параллелограмма
	Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Свойство: равенство противолежащих сторон
	Если четырёхугольник является параллелограммом, то его противолежащие стороны равны
Признак: равенство противолежащих сторон
	Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом
Признак: равенство и параллельность двух противолежащих сторон
	Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом
Свойство: диагонали точкой пересечения делятся пополам
	Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам
Признак: диагонали точкой пересечения делятся пополам
	Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом
Свойство: суммы углов, прилежащих к сторонам
	Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°
Признак: суммы углов, прилежащих к сторонам
	Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180° , то четырёхугольник является параллелограммом
Свойство: равенство противолежащих углов
	Если четырёхугольник является параллелограммом, то его противолежащие углы равны
Признак: равенство противолежащих углов
	Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом
Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника
Признак: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом
Свойство: четыре треугольника, на которые диагонали делят четырёхугольник
	Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак: четыре треугольника, на которые диагонали делят четырёхугольник
	Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом

Параллелограмм

Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны

Диагонали параллелограмма

Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины

Высота параллелограмма

Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение

Равенство противолежащих сторон

Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны.

Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом.

Равенство и параллельность двух противолежащих сторон

Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом.

Диагонали точкой пересечения делятся пополам

Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам.

Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом.

Суммы углов, прилежащих к сторонам

Свойство: Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° .

Признак: Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180° , то четырёхугольник является параллелограммом.

Равенство противолежащих углов

Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны.

Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом.

Два треугольника, на которые каждая диагональ делит четырёхугольник

Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника.

Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом.

Четыре треугольника, на которые диагонали делят четырёхугольник

Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)

Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом.

Свойства и признаки прямоугольника

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Прямоугольник		Прямоугольником называют параллелограмм, у которого все углы прямые
Свойство	Равенство диагоналей		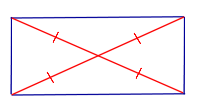Если параллелограмм является прямоугольником, то его диагонали равны
Признак			Если у параллелограмма диагонали равны, то он является прямоугольником

Определение: прямоугольник
	Прямоугольником называют параллелограмм, у которого все углы прямые
Свойство: равенство диагоналей
	Если параллелограмм является прямоугольником, то его диагонали равны
Признак: равенство диагоналей
	Если у параллелограмма диагонали равны, то он является прямоугольником

Прямоугольник

Определение: Прямоугольником называют параллелограмм, у которого все углы прямые.

Равенство диагоналей

Свойство: Если параллелограмм является прямоугольником, то его диагонали равны.

Признак: Если у параллелограмма диагонали равны, то он является прямоугольником.

Свойства и признаки ромба

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Ромб		Ромбом называют параллелограмм, у которого все стороны равны
Свойство	Биссектрисы углов диагонали		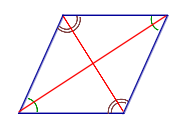Если параллелограмм является ромбом, то его диагонали является биссектрисами углов
Признак			Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство	Перпендикулярность диагоналей		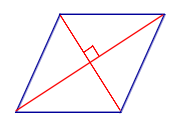Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак			Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Определение: ромб
	Ромбом называют параллелограмм, у которого все стороны равны
Свойство: биссектрисы углов и диагонали
	Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов
Признак: биссектрисы углов и диагонали
	Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство: перпендикулярность диагоналей
	Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак: перпендикулярность диагоналей
	Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Ромб

Определение: Ромбом называют параллелограмм, у которого все стороны равны

Биссектрисы углов и диагонали

Признак: Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом

Перпендикулярность диагоналей

Свойство: Если параллелограмм является ромбом, то его диагонали перпендикулярны

Признак: Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Свойства и признаки квадрата

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Квадрат		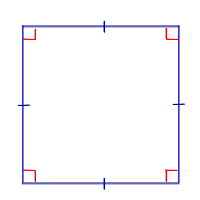Квадратом называют параллелограмм, у которого все стороны равны и все углы равны
Свойство	Перпендикулярность и равенство диагоналей		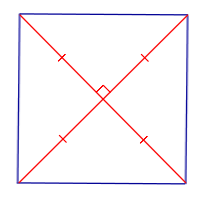Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак			Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом
Свойство	Перпендикулярность диагоналей		Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак			Если у прямоугольника диагонали перпендикулярны, то он является квадратом
Свойство	Равенство диагоналей		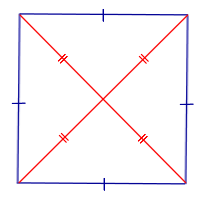Если ромб является квадратом, то его диагонали равны
Признак			Если у ромба диагонали равны, то он является квадратом

Определение: квадрат
	Квадратом называют параллелограмм, у которого все стороны равны и все углы равны
Свойство: перпендикулярность и равенство диагоналей
	Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак: перпендикулярность и равенство диагоналей
	Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом
Свойство: перпендикулярность диагоналей
	Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак: перпендикулярность диагоналей
	Если у прямоугольника диагонали перпендикулярны, то он является квадратом
Свойство: равенство диагоналей
	Если ромб является квадратом, то его диагонали равны
Признак: равенство диагоналей
	Если у ромба диагонали равны, то он является квадратом

Квадрат

Определение: Квадратом называют параллелограмм, у которого все стороны равны и все углы равны

Перпендикулярность и равенство диагоналей

Свойство: Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны

Признак: Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом

Перпендикулярность диагоналей

Свойство: Если прямоугольник является квадратом, то его диагонали перпендикулярны

Признак: Если у прямоугольника диагонали перпендикулярны, то он является квадратом

Равенство диагоналей

Свойство: Если ромб является квадратом, то его диагонали равны

Признак: Если у ромба диагонали равны, то он является квадратом

Урок геометрии «Равновеликие фигуры в решении задач»

Разделы: Математика

Цель урока:

• повторение и обобщение ключевых задач о равновеликих фигурах;
• обучение учащихся поиску решения задач в ходе создания проблемно-познавательной ситуации;
• развитие грамотной устной и письменной математической речи учащихся.

Оборудование: доска, с заготовленными чертежами или слайды; раздаточный материал: учебное пособие Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса.

Ход урока

Заканчивая изучение темы «Площади», сегодня мы повторяем и развиваем наши знания о равновеликих фигурах.

1. Чтобы вспомнить понятие «равновеликие фигуры», поиграем в «Да» и «Нет».

Я составила диктант-попурри, выбрав вопросы из ваших диктантов, связанных с этим понятием. Я читаю вопрос, его автор комментирует правильный ответ.

Учащимся к семинару по теме «Площади» было предложено домашнее задание: составить диктант из пяти вопросов по данной теме, ответы на которые предполагали либо «да», либо «нет». Данную работу можно было выполнять группами по два человека, увеличив количество вопросов. Для быстрой проверки умения оперировать с понятиями при проведении диктантов используются сигнальные карточки: треугольники белого цвета и цветные треугольники, вырезанные из бумаги, при ответе «Да» учащиеся поднимают карточку белого цвета, при ответе «Нет» — цветной треугольник.

• Верно ли, что фигуры, имеющие равные площади, называются равновеликими?
• Верно ли, что равные многоугольники равновелики?
• Верно ли, что если площади фигур равны, то и фигуры равны?
• Могут ли равновеликие фигуры быть равными?
• Верно ли, что диагонали параллелограмма делят его на четыре равновеликих треугольника?

2. Какие ключевые (базовые) задачи о равновеликих треугольниках мы рассматривали?

№1. Медиана треугольника разделяет его на два равновеликих треугольника.

Обоснуйте это утверждение (открыть заготовленный рис. №1 и по ходу обоснования сделать запись, рисунок не стирать).

№2. Все треугольники с общим основанием, вершины которых лежат на прямой, параллельной основанию, равновелики.

Обоснуйте это утверждение (открыть рис. №2 и по ходу обоснования сделать запись, рисунок не стирать).

1) На рисунке 3 я начертила ломаную ADB. Сравните площади четырёхугольников ADBС и ADBХ, ответ обоснуйте.

Вывод:

Сколько четырёхугольников равновеликих четырёхугольнику ADBC можно построить на рисунке 3?

Ответ: бесконечно много.

Что для этого надо сделать?

Ответ: отметить точку на прямойm и соединить её с точками A и B.

Полученный четырёхугольник будет равновелик четырёхугольнику ADBC.

Какой результат я могла бы получить, если бы дополнила рисунок 3 ломаной из

3-х звеньев? 4-х звеньев?

Ответ: бесконечно много равновеликих пятиугольников, шестиугольников и т.д.

Показать рисунок 4.

2) Начертите выпуклый четырёхугольник ABCD. Проведите диагональ AC. (рис.5)

Как построить четырёхугольник, равновеликий четырёхугольнику ABCD, диагональ которого есть отрезок AC?

Ответ: провести прямую а такую, что а ll АС, и D.

Пусть E, четырёхугольник ABCD равновелик четырёхугольнику ABCE.
Докажите последнее утверждение.

3) Есть ли на Рис. 6 равновеликие треугольники?

Какое утверждение позволяет нам это доказать?

Пусть .

Можно ли выразить площадь четырёхугольника ABCO через и ?

Ответ: да,

Можно ли выразить площадь четырёхугольника ABCO через ?

Ответ: да,

Как связаны ?

Ответ:

4) Решим задачу о разбиении данного выпуклого четырёхугольника на две равновеликие части.

Прочитаем условие задачи № 130 [1]

№ 130. В выпуклом четырёхугольнике ABCD через середину O диагонали BD проведена прямая, параллельная диагонали AC. Она пересекает сторону AD в точке E.

Докажите, что .

Сделаем чертёж (рис.7).

На рисунке отметим, что точка О – середина BD и укажем, что EO ll AC. Итак, что мы должны доказать? . Обозначим . Какую часть должна составлять площадь каждой фигуры от S? Проанализируем условие, подумаем: по условию точка О – середина BD, какое утверждение, связанное с равносильностью фигур, мы могли бы использовать?

Ответ: медиана делит треугольник на два равновеликих треугольника.

Что нам надо провести на чертеже, чтобы можно было это утверждение применить?

Ответ: медианы АО и СО.

1. Проведём АО и СО.
2. 
3. по свойству медианы.
4. , по свойству 2 площадей.
   Какое условие мы не использовали?
   Ответ: EO ll AC.
   Можем ли мы сравнить площади четырёхугольников ABCE и ABCO?
5. т.к. EO ll AC, то , , .
6. , , значит, по свойству 2 площадей , ч.т.д.

Итог урока

Сегодня мы посвятили урок равновеликим многоугольникам. А где это может нам понадобиться, где практически можно применить полученные знания?

Пусть пройдёт какое-то время и кому-то из вас доведётся стать землеустроителем. Всем известно, что земледельцу не важно, какой формы участок, важна его площадь.

Допустим, что надо решить задачу: разделить участок на две части, равные по площади, если участок имеет форму: а) треугольника; б) четырёхугольника, при условии, что граница должна проходить через вершину многоугольника (столб на участке, например, стоит в этой вершине, и никому не хочется иметь его на своей земле).

Как выгоднее проводить границу: в виде ломаной или в виде отрезка прямой?

Ответ: длина отрезка меньше длины ломаной, соединяющей его концы, значит, если граница пройдёт по отрезку, то меньше материала уйдёт на ограждение.

Сформулируйте поставленную задачу на языке геометрии.

Ответ: а) Разделить треугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Ответ: Провести медиану из этой вершины.

Ответ: б) Разделить четырёхугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Решить задачу №130.

1. Провести АС.
2. Провести ВD.
3. Отметить точку О середину ВD.
4. Провести прямую mтакую, чтоm ll AC,
5. m пересекает CD в точке М
6. АМ – искомая граница.

Как разделить на две равновеликие части участок, имеющий форму пятиугольника?

Литература

1. Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса. М.: Просвещение, 1996.

🎥 Видео