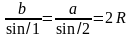Дельтоид вписанный в окружность свойства

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дельтоид

Автор работы награжден дипломом победителя III степени

На уроках геометрии в первой четверти 8 класса мы изучали различные четырехугольники, такие как параллелограмм, прямоугольник, квадрат, ромб и трапеция. Мы доказывали их свойства и признаки, с помощью которых потом решали различные задачи. Возник вопрос: все ли виды четырехугольников мы изучили? Пытаясь ответить на этот вопрос, в сети Интернет я наткнулась на еще один четырехугольник – дельтоид. Проведя анализ привычных школьных справочников, а также заглянув в знаменитый справочник Бронштейна, я не нашла никаких сведений о дельтоиде. Между тем эту фигуру мы часто встречаем в окружающем мире, например, крона дерева туя (рис.1), тело рыбы (рис.2), человеческий мозжечок (рис.3), соединенные человеческие руки (рис.4), воздушный змей (рис.5), лист дерева (ри.6), а также форма носа и глаза.

рис.1 рис.2 рис.3 рис. 4

Меня очень заинтересовал данный четырехугольник, и я решила глубже узнать, что это за дельтоид, сформулировать и доказать его свойства и признаки, решить различные задачи с ним, а потом представить свои разработки в виде сайта для своих одноклассников и всех тех, кто интересуется геометрией.

Цель: изучение четырехугольника дельтоид и создание сайта «Все о дельтоиде».

— познакомиться с литературой по данной теме;

— сформулировать различные определения дельтоида;

— сформулировать свойства и признаки дельтоида;

— составить и решить задачи с дельтоидом;

— составить тесты для проверки знаний о дельтоиде;

— создать электронный образовательный ресурс — сайт «Все о дельтоиде», содержащий теоретический и практический материал по данной теме.

Объект исследования: четырехугольник дельтоид.

Предмет исследования: определение, свойства и признаки дельтоида.

Методы исследования: работа с научной литературой, анализ и систематизация теоретического материала, решение задач.

Глава 1. Дельтоид – один из видов четырехугольников

1.1 Определение дельтоида

Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта ).

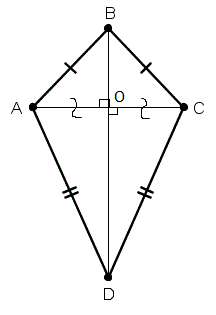
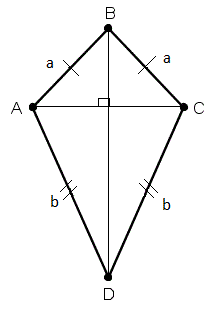
Изучив различную литературу по данной теме, я выделила два определения дельтоида (рис.7):

— Дельтоид — четырёхугольник, у которого есть две пары равных соседних сторон.

— Дельтоид – это четырехугольник, симметричный относительно одной из своих диагоналей. [4,5,6,8]

Из определения дельтоида следует, что ромб и квадрат также являются дельтоидами.

Главная диагональ дельтоида — это отрезок, соединяющий вершины неравных углов дельтоида. Неглавной диагональю дельтоида называют вторую диагональ дельтоида.

Средняя линия дельтоида это – отрезок, соединяющий середины соседних сторон дельтоида.

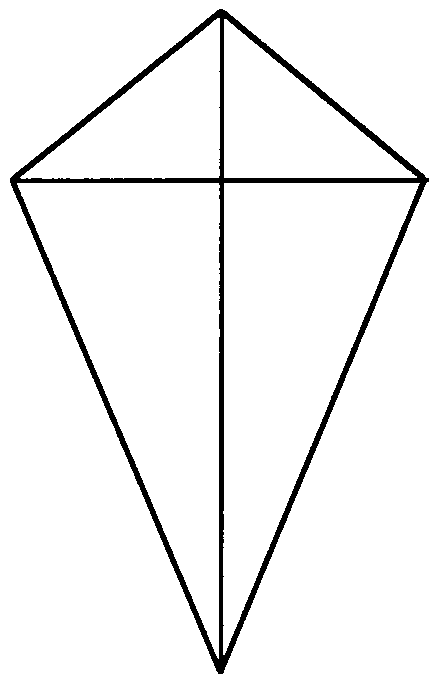
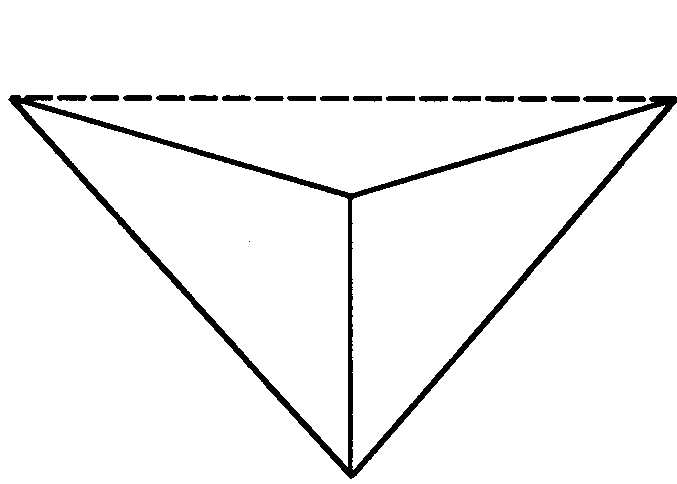
Есть два вида дельтоидов: выпуклый (рис.7) и невыпуклый (рис.8).

Все углы выпуклого дельтоида меньше развёрнутого угла, а один из углов невыпуклого дельтоида больше развёрнутого угла.

1.2 Свойства дельтоида

Изучив литературу, по данной теме, мною были выделены следующие свойства дельтоида (табл.1).

Табл.1 Свойства дельтоида

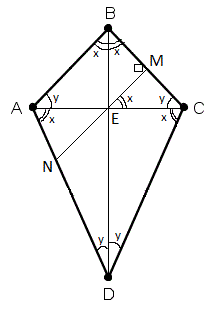
1) Углы дельтоида между сторонами разной длины имеют равную величину

2) Диагонали дельтоида перпендикулярны друг другу, одна из них делит другую на две равные части

3) Во всякий выпуклый дельтоид можно вписать окружность, и только одну

4) Неглавная диагональ делит дельтоид на два равнобедренных треугольника

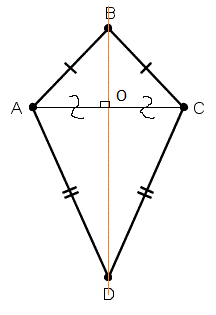
5) Главная диагональ дельтоида является биссектрисой противолежащих углов

6) Главная диагональ делит дельтоид на два равных треугольника

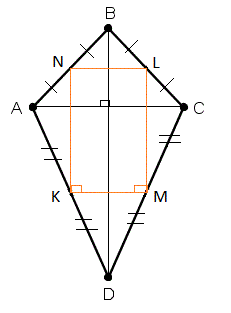
7) Средние линии дельтоида образуют прямоугольник, периметр которого равен сумме диагоналей данного дельтоида

8) Площадь дельтоида равна половине произведения диагоналей

9) Площадь дельтоида равна произведению двух его неравных сторон на синус угла между ними

Проведя сравнительный анализ со свойствами изученных четырехугольников, я выделила общие свойства дельтоида, ромба и квадрата:

— диагонали взаимно перпендикулярны;

— площадь равна половине произведения диагоналей;

— средние линии образуют прямоугольник, периметр которого равен сумме диагоналей данного дельтоида.

Также в любой выпуклый дельтоид, как и в квадрат, можно вписать окружность, и только одну.

Мною были определены и различия в свойствах дельтоида и других изученных четырехугольников. У дельтоида:

— только одна пара равных противолежащих углов (у параллелограмма, прямоугольника, ромба, квадрата – две);

— только одна диагональ точкой пересечения диагоналей делится пополам (у параллелограмма, прямоугольника, ромба, квадрата – обе диагонали);

— только главная диагональ делит на два равных треугольника (у параллелограмма, прямоугольника, ромба, квадрата – обе диагонали);

— только главная диагональ дельтоида является биссектрисой противолежащих углов (у ромба – обе диагонали);

— только неглавная диагональ делит дельтоид на два равнобедренных треугольника (у квадрата и ромба – обе диагонали).

1.3 Признаки дельтоида

Можно выделить четыре признака дельтоида (табл.2).

Табл.2 Признаки дельтоида

1)Если у четырёхугольника только одна ось симметрии, проходящая через диагональ, то это дельтоид

2) Если четырёхугольник образован двумя равнобедренными треугольниками с разными боковыми сторонами и общим основанием, то это дельтоид

3) Если у четырехугольника диагонали взаимно перпендикулярны и только одна из них делит другую пополам, то это дельтоид

4) Если в четырёхугольнике только одна диагональ является биссектрисой противоположных углов, то это дельтоид

1.4 Задачи с дельтоидом

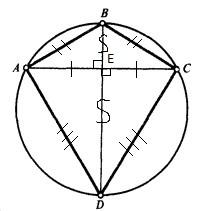
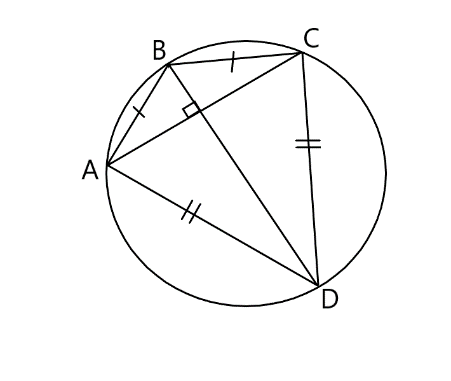
Изучив некоторые российские учебные пособия по математике [1], я не встретила системы задач про дельтоид. Однако мы встречались с этой геометрической фигурой на уроках геометрии еще в 7 классе (УМК по ред. А.Г.Мерзляка [2,3]), когда решали задачи на применение признаков равенства треугольников (№161 (рис.9), №176 (рис.10)) и задачи по теме «Касательная к окружности» (№523 (рис.11)).

рис.9 рис.10 рис.11

Изучив признаки и свойства дельтоида, я попыталась составить достаточное количество разнообразных и интересных задач с дельтоидом вычислительного характера. Примеры таких задач приведены ниже, для некоторых из них рассмотрено решение. [7]

Одна из диагоналей дельтоида равна 16 см, а его площадь – 120 см 2 . Чему равна длина второй диагонали дельтоида?

120 = ·16· d ₂; 120 = 8· d ₂; d ₂ = 120 : 8; d ₂ = 15 см

Найти стороны дельтоида, если его периметр

равен 116 см, а разность боковых сторон равна

Ответ: АВ=30,5 см; ВС=30,5 см; CD =27,5 см; AD =27,5 см

На сторонах АВ и ВС прямоугольника АВС D взяты точки К и О соответственно так, что КВ = ВО, а на стороне А D взята точка Е так, что КЕ = ОЕ. Найти АВЕ.

1)В = 90°, так как АВС D — прямоугольник.

2)Рассмотрим четырёхугольник КВОЕ.

КВ=ОВ (по условию); КЕ=ОЕ (по условию).

Значит, КВОЕ – дельтоид по определению.

3)ВЕ – главная диагональ дельтоида, следовательно, она является биссектрисой противолежащих углов дельтоида, т.е. АВЕ= В. Значит, АВЕ= · 90° = 45°.

На сторонах АВ, ВС и АС треугольника АВС отмечены точки F , D и E такие, что ЕС : АЕ = 2 : 1, F Е = D Е, А F = 2 см, D С = 5 см, F В = В D . Найдите F В.

1) Так как FE = DE , FB = BD по условию, то BDEF – дельтоид по определению.

2) BE – главная диагональ дельтоида, а, значит, и биссектриса B (по свойству дельтоида).

По свойству биссектрисы или .

Пусть FB = BD =х, тогда

Равные стороны АВ и ВС дельтоида АВС D перпендикулярны и равны

2 см, К – точка пересечения диагоналей АС и В D , АК = КС. Из точки К проведен перпендикуляр КЕ к стороне С D , СЕ = 1 см. Найдите Е D .

∆ ABC – равнобедренный прямоугольный

треугольник, т.к. AB = BC и АВ ВС. По теореме Пифагора + = ,

2) Т.К. АК = КС по условию, то АК = КС = 2 см. рис.15

3) AC BD по свойству дельтоида, значит, ∆ KCD – прямоугольный.

КС² = CE ∙ CD (по теореме о пропорциональных отрезках в прямоугольном треугольнике)

1.5 Тесты по теме «Дельтоид»

Рассмотрев свойства и признаки дельтоида, изучив возможность их применения для решения задач, я составила тесты для проверки знаний по теме «Дельтоид».

Обобщающий тест «Всё о дельтоиде»

Форму какого из четырехугольников имеет мозжечок человека:

Выберите верное утверждение:

Дельтоид – это четырехугольник, у которого стороны попарно равны

Дельтоид – это четырехугольник, у которого есть две пары равных соседних сторон

Дельтоид – это четырехугольник, у которого диагонали взаимно перпендикулярны

Дельтоид – это четырехугольник, у которого две стороны равны

Выберите неверное утверждение:

Главная диагональ дельтоида – это отрезок, соединяющий вершины неравных углов дельтоида

Дельтоид – это четырехугольник, в котором две пары соседних сторон равны

Неглавная диагональ дельтоида – это отрезок, соединяющий вершины равных углов дельтоида

Средняя линия дельтоида – это отрезок, соединяющий стороны дельтоида

Какой четырехугольник может быть невыпуклым:

Выберите верное утверждение:

Если в четырехугольнике две стороны равны, то это дельтоид

Если четырехугольник образован двумя равнобедренными треугольниками с разными боковыми сторонами и общим основанием, то это дельтоид

Если в четырехугольнике диагонали является биссектрисами противолежащих углов, то это дельтоид

Если в четырехугольнике есть пара равных соседних сторон, то это дельтоид

Выберите неверное утверждение:

Все углы дельтоида равны

Углы дельтоида между сторонами разной длины имеют равную величину

Площадь дельтоида равна половине произведения его диагоналей

Главная диагональ делит дельтоид на два равных треугольника

Выберите верное утверждение:

Около всякого выпуклого дельтоида можно описать окружность

Все стороны дельтоида равны

Неглавная диагональ делит дельтоид на два равнобедренных треугольника

В выпуклом дельтоиде один из углов больше развёрнутого

У какого четырехугольника только одна диагональ является биссектрисой противолежащих углов:

В дельтоиде смежные стороны относятся как 3 : 5. Найдите большую сторону дельтоида, если его периметр равен 48 см.

Одна из диагоналей дельтоида равна 18 см, а его площадь – 234 см 2 . Чему равна длина второй диагонали дельтоида?

Какого из перечисленных элементов нет у дельтоида?

Радиус описанной окружности

Радиус вписанной окружности

АВС D – дельтоид. Треугольник АВС равносторонний, и его периметр равен 30 см. Треугольник АС D – равнобедренный, и его периметр равен 46 см. Найдите периметр дельтоида АВС D .

1.6 Создание электронного образовательного ресурса – сайт «Все о дельтоиде»

Проделав работу по формулированию и доказательству свойств и признаков дельтоида, составлению и решению задач на вычисление различных величин в дельтоиде, созданию тестов по теме «Дельтоид», весь разработанный материал я оформила в виде сайта «Все о дельтоиде», размещенного по адресу https://sites.google.com/view/deltoid-na5 .

Данный сайт можно использовать для объяснения материала о дельтоиде на уроках геометрии и во внеурочной деятельности, для самостоятельного изучения обучающимися этой темы с последующей проверкой полученных знаний в ходе решения интерактивных тестов.

Данный сайт состоит из шести разделов:

1 раздел — Главная страница (рис. 16) — содержит общую информацию о создателе сайта, а также рассмотрены примеры дельтоидов из окружающей обстановки.

2 раздел — «Что такое дельтоид» (рис.17), в котором приведены различные определения дельтоида, рассмотрены его элементы.

3 и 4 разделы — «Свойства дельтоида» и «Признаки дельтоида» (рис.18. рис.19). В этих разделах сформулированы характерные для дельтоида свойства и признаки.

5 раздел – «Задачи и дельтоидом» (рис.20). На этой странице приведены решения некоторых задач на вычисление различных элементов дельтоида, а также предложены задачи для самостоятельного решения.

6 раздел – «Тесты по теме «Дельтоид» (рис.21, рис.22). В этом разделе можно проверить свои знания по данной теме с помощью предложенных интерактивных тестов.

На одном из уроков геометрии я предложила своим одноклассникам познакомиться с дельтоидом, изучив материал на сайте «Все о дельтоиде» (рис.23, рис.24, рис. 25).

рис.23 рис.24 рис.25

Мне было очень интересно узнать мнение ребят о моем электронном образовательном ресурсе – сайте «Все о дельтоиде». Вот некоторые из высказываний.

Таня Т.: «Очень интересно было узнать об еще одном четырехугольнике – дельтоиде».

Оля П.: «Информация изложена доступно и понятно. Понравилось самостоятельно решать задачи с дельтоидом».

Антон Р.: «Оказывается, что дельтоид окружает нас повсюду».

Настя К.: «Изучив определение, свойства и признаки дельтоида и решив задачи для самостоятельной работы, я практически без ошибок прошла интерактивное тестирование».

В данной работе изучена неизвестная в школьном курсе математики геометрическая фигура – дельтоид, которая, однако, встречается очень часто в нашей жизни. Была проделана работа по формулированию свойств и признаков этого четырехугольника, составлено достаточное количество разнообразных задач на вычисление различных элементов дельтоида, также были разработаны тесты для оценки знаний по данной теме. Весь накопленный материал я оформила в виде электронного образовательного ресурса – сайта «Все о дельтоиде», который был предложен моим одноклассникам на одном из уроков геометрии и получил положительные отзывы.

Таким образом, цели, стоящей перед нами, мы достигли – изучен четырехугольник дельтоид. Я бы порекомендовала использовать созданный электронный продукт на урочной и внеурочной деятельности для объяснения материала по данной теме, самостоятельного изучения обучающимися этой темы с последующей проверкой полученных знаний в ходе выполнения интерактивных тестов.

Киселев А.П. Геометрия / Под ред. Н.А.Глаголева.-М.:ФИЗМАТЛИТ,2013.-328с.

Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 7 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2017

Мерзляк А.Г., Полонский В.Б., Якир М.С. и др. Геометрия 8 класс: учеб. для общеобразоват. организаций.- М.: Вентана-Граф, 2018

Перельман Я.И. Занимательная алгебра, геометрия. М.: Книга, 2005

Титаренко А.М., Роганин А.Н. Новейший полный справочник школьника:5-11 классы.-М.:Эксмо, 2008.-304с.

Цыпкин А.Г. Справочник по математике для средней школы.-М.: Наука. Главная редакция физико-математической литературы, 1981.-400с.

Шноль Д, Сгибнев А, Нетрусова Н. Система открытых задач по геометрии: 8 класс – М.: Чистые пруды, 2009. – 32 с.: ил. – (Библиотечка «Первого сентября», серия «Математика». Вып. 29).

Энциклопедический словарь юного математика / Сост. А.П.Савин. -М.:Педагогика,1989.-352с.

http :// math 4 school . ru / chetyrehugolniki . html

Видео:Четырехугольник, которому не повезло | дельтоид (недоромб)Скачать

Дельтоид.

Дельтоид — четырехугольник, который содержит 2 пары смежных сторон, имеющих одинаковую длину.

Дельтоид бывает выпуклым или невыпуклым:

На рисунке слева изображен выпуклый дельтоид, справа — невыпуклый.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства дельтоида.

1. Углы меж сторонами разной длины имеют равную величину.

2. Диагонали дельтоида перпендикулярны друг другу.

3. Во всякий выпуклый дельтоид вписывается окружность, а также, если дельтоид имеет вид ромба, то есть еще одна окружность, которая касаюется продолжений всех 4-х сторон. Для невыпуклого дельтоида может быть построена окружность, которая касается 2-х бОльших сторон и продолжений 2-х меньших сторон и окружность, которая касается 2-х меньших сторон и продолжений 2-х бОльших сторон.

4. Одна диагональ точкой пересечения делится на две равные части.

5. Одна диагональ оказывается биссектрисой углов.

6. Одна диагональ разделяет дельтоид на 2 равнобедренных треугольника.

7. Одна диагональ разделяет дельтоид на 2 равных треугольника.

8. Прямые, которые содержат диагонали всех дельтоидов, пересекаются под углом, равным 90 градусам.

Во всякий выпуклый дельтоид вписывается окружность.

Если выпуклый дельтоид не оказывается ромбом, значит, есть окружность, которая касается продолжений каждой их 4-х сторон нашего дельтоида.

Для невыпуклого дельтоида строится окружность, которая касается 2-х сторон большей длины и продолжений 2-х меньших сторон, а также окружность, которая касается 2-х меньших сторон и продолжений 2-х сторон большей длины.

Около дельтоида описывается окружность только в том случае, если его стороны, имеющие разные длины, образуют углы по 90 градусов.

Радиус окружности, которая описана вокруг дельтоида можно вычислить через 2 его разные стороны:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Площадь дельтоида.

Площадь всякого дельтоида определяют:

• через диагонали дельтоида:

• через 2 соседние разные стороны и угол между ними:

где a и b длины разных сторон, а α угол между ними.

Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Частные случаи.

1. Когда угол меж разных сторон дельтоида равен 90 градусам, значит, около него можно описать окружность (вписанный дельтоид).

2. Когда пара противоположных сторон дельтоида имеют равную величину, значит, этот дельтоид называется ромбом.

3. Когда пара противоположных сторон и 2 диагонали дельтоида имеют равные величины, то дельтоид является квадратом. Квадратом оказывается и вписанный дельтоид с равными диагоналями.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Проект «Неизвестный дельтоид»

Существуют различные виды классификаций четырехугольников, например, по параллельности сторон выделяют параллелограмм и трапецию, по равенству сторон – ромб и квадрат, по равенству всех углов – квадрат и прямоугольник, все эти фигуры изучаются в школьной программе.

Изучая литературу, решая геометрические задачи, я обратила внимание, что четырехугольник, у которого диагонали перпендикулярны, но он не является ромбом, обладает рядом интересных свойств. Этот четырехугольник – дельтоид.

Просмотр содержимого документа
«Проект «Неизвестный дельтоид»»

Муниципальное общеобразовательное учреждение

Малодубенская средняя общеобразовательная школа №7

Итоговый проект по геометрии

Тема: «Неизвестный дельтоид»

Обучающейся 9 класса

Романовой Ирины Александровны

Романова Людмила Геннадьевна

Первое свойство. 4

Второе свойство. 4

Третье свойство. 5

Четвертое свойство. 5

Пятое свойство. 5

Первый признак. 6

Второй признак. 6

Площадь дельтоида. 7

Первая формула. 7

Вторая формула. 7

Третья формула. 8

Четвертая формула. 8

Окружность, вписанная в дельтоид. 9

Окружность, описанная около дельтоида. 9

Примеры решения задач. 11

Список используемой литературы. 14

Существуют различные виды классификаций четырехугольников, например, по параллельности сторон выделяют параллелограмм, у которого попарно параллельны все стороны, и трапецию — параллельны две стороны, по равенству сторон выделяют ромб и квадрат, по равенству всех углов – квадрат и прямоугольник и т.д., эти фигуры изучаются в школьной программе.

Изучая литературу, решая геометрические задачи, я обратила внимание на то, что четырехугольник, у которого диагонали перпендикулярны, но не является ромбом, обладает рядом интересных свойств. Этот четырехугольник – дельтоид.

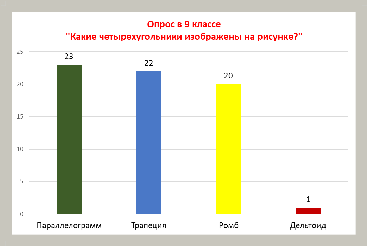
В своем классе я провела опрос по определению геометрических фигур: трапеция, параллелограмм, ромб и дельтоид. Участие приняли 25 человек. Результаты опроса отображены на диаграмме.

Поэтому целью моего проекта является: изучить дельтоид и рассмотреть применение его в окружающем мире.

Для выполнение этой цели были поставлены следующие задачи:

Дать определение дельтоида.

Изучить свойства и признаки дельтоида.

Рассмотреть задачи, которые решаются с дельтоидом.

Найти практическое применение.

Дельтоид – четырехугольник, обладающий двумя парами смежных сторон одинаковой длины, диагонали пересекаются под прямым углом. Дельтоид иначе называют ромбоидом. Название дельтоид происходит от названия греческой буквы (дельта).

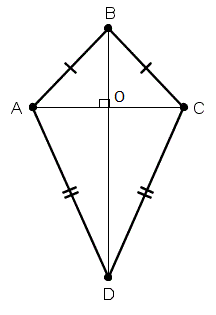
У дельтоида одна пара противолежащих углов равна. (Углы, лежащие по разные стороны от главной диагонали равны.)

Дано: ABCD – дельтоид

∆ABC –равнобедренный, AC — основание,

∆ADC –равнобедренный, AC — основание,

Большая диагональ является биссектрисой.

Дано: ABCD – дельтоид

Доказать: BD – биссектриса

1) ∆BAD = ∆BCD (по 1 призн), т.к.

AB = CB, AD = CD, /BAD = /BCD

3) BD – биссектриса.

Третье свойство.

Диагонали дельтоида пересекаются, и точкой пересечения меньшая диагональ делится пополам.

Дано: ABCD – дельтоид

1) т.к. ∆BAD = ∆BCD (аналогично в 1 свойству)

2) AO – высота ∆BAD, CO – высота ∆BCD (диагонали BD┴AC)

3) высоты равных треугольников тоже равны AO=CO

Осью симметрии дельтоида является большая диагональ.

Дано: ABCD – дельтоид

Доказать: BD – ось симметрии

Док-во: 1) рассмотрим симметрию относительно BD.

2) точка D перейдет в саму себя.

3) точка A перейдет в точку C, т.к. AO = OC и BD|AC

4) точка B перейдет в саму себя

5) точка C перейдет в точку A, т.к. AO = OC и BD|AC

6) ∆BAD перейдет в ∆BCD

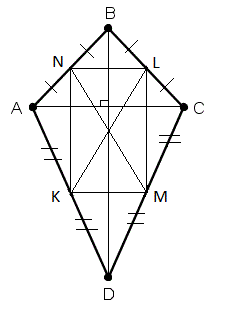
Параллелограммом Вариньона, построенный в серединах сторон дельтоида, является прямоугольник.

Дано: ABCD – дельтоид

Найти: определить вид четырехугольника KLMN

Решение: 1) рассмотрим ∆BAD,

KN — средняя линия, KN||BD,

2) рассмотрим ∆BCD,

LM — средняя линия,

4) так как BD|AC, то KN|NL, LM|KM.

5) KLMN- прямоугольник

Признаки. Первый признак.

Теорема 1. Если одна из диагоналей четырехугольника является биссектрисой одного из его углов и делит периметр четырехугольника пополам, то четырехугольник есть дельтоид.

Дано: ABCD — четырехугольник

BD — биссектриса /ABD

Доказать: ABCD — дельтоид

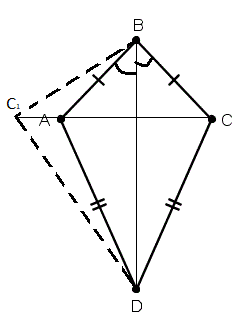
Доказательство: (от противного)

Предположим, что A и C – не симметричны, относительно BD.

Построим C₁, симметричную точке C (C_{1 =} A).

Так как периметры равны, т.е. P_BCD=P_BAC=P_BC1D, то приходим к противоречию. Значит A-C₁

Теорема 2. Если у четырехугольна, вписанного в окружность, ось симметрии совпадает с диагональю, то он является дельтоидом.

Дано: ABCD — четырехугольник

Окружность (O, R) – описанная

BD – диагональ = ось симметрии

Доказать: ABCD — дельтоид

Т.к. BD — ось симметрии, то A-C, значит AC-BD

∆ABE = ∆CBE (по 1 признаку: AE=CE, BE – общая, /BEA=/BEC=90), значит AB=BC

∆AED = ∆CED (по 1 признаку: AE=CE, DE – общая, /AED=/CED=90), значит AD=CD

Площадь дельтоида. Первая формула.

S= 1/2AO*BO + 1/2BO*CO + 1/2AO*DO + 1/2CO*DO= =1/2BO(AO+CO)+1/2BO*AC+1/2DO*AC= =1/2AC(BO+DO)= 1/2AC*BD=1/2d_1*d₂

Известным индийским математиком Брахмагуптой (около 598 года н.э.) было установлена формула площади вписанного в окружность четырехугольника, а именно:

S=√(p-a)(p-b)(p-c)(p-d), где p=(a+b+c+d)/2 – полупериметр четырехугольника. Эта формула является обобщенным случаем известной формулы площади треугольника.

Применим данную формулу для вписанного в окружность дельтоида. Так как a=b и c=d получаем, что S=(p-a)(p-b). Докажем это.

1) По теореме косинусов AC 2 = a 2 + a 2 -2a 2 *cos /B=

AC 2 = 2a 2 + 2a 2 -2a 2 *cos /B= 2b 2 + 2b 2 -2b 2 *cos /D.

2) Т.к. ABCD – вписанный четырехугольник, то /D=180 0 —/B, поэтому cos /D= -cos /B, sin /D=sin /B, следовательно, 2a 2 -2a 2 *cos /B= 2b 2 -2b 2 *cos /D.

2(a 2 -b 2 ) = 2cos /B(a 2 +b 2 )

a 2 -b 2 = (a 2 +b 2 ) cos /B (1)

Площадь четырехугольника равна сумме площадей треугольников, на который он разбивается своей диагональю, то есть

S = 1/2*a 2 *sin /B+1/2*b 2 *sin /D = ½ (a 2 + b 2 ) sin /B или

2S = (a 2 + b 2 ) sin /B (2)

Возведем неравенства (1) и (2) в квадрат и сложим их, учитывая, что cos 2 /B + sin 2 /B = 1, получим

4S 2 + (a 2 — b 2 ) 2 = (a 2 + b 2 ) 2

4S 2 = (a 2 + b 2 ) 2 — (a 2 — b 2 ) 2

4S 2 = (a 2 + b 2 — a 2 + b 2 ) (a 2 + b 2 + a 2 — b 2 )

4S 2 = 2a 2 * 2b 2

Это доказательство проводилось по рассуждениям древнего математика Брахмагупты, эту же формулу можно вывести короче:

Т.к. дельтоид вписан в окружность, то большая диагональ является диаметром, значит она разбивает четырехугольник на два равных прямоугольных треугольника (вписанный угол, опирающийся на диаметр равен 90 ⸰ ). Площадь прямоугольного треугольника равна S=12ab, значит площадь дельтоида равна S=ab.

Площадь вписанного дельтоида можно найти другим способом. Докажем теорему: если дельтоид со сторонами a, b, вписан в окружность радиуса R, то его площадь равна

Пусть диагонали дельтоида равны x и y.

Воспользовавшись формулой S= abc/4R, где a,b,c, — стороны треугольника, а R- радиус описанной окружности, получаем:

S_ABCD = abx/2R (1) или S_ABCD = a 2 y/4R+ b 2 y/4R (2)

Перемножив неравенства (1) и (2), получаем:

S_ABCD = abx/2R*(a 2 y/4R+ b 2 y/4R) = 1/8R 2 * ab(a 2 +b 2 ) * xy = 1/8R 2 * 2a 2 b 2 (a 2 + b 2 ) = 1/4R 2 * a 2 b 2 (a 2 + b 2 ) (так как по теореме Птолемея xy = ac+bd, то есть xy = 2ab), значит S = .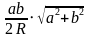

Площадь параллелограмма Вариньона равна половине площади дельтоида.

так как KL – средняя линия треугольника ABC и LM – средняя линия треугольника BCD.

Окружность, вписанная в дельтоид.

Докажем, что в дельтоид можно вписать окружность.

В четырехугольник можно вписать окружность, если суммы противолежащих сторон равны. Действительно, т.к. AB=BC и CD=AD, то AB+CD=BC+AD.

Окружность, описанная около дельтоида.

В дельтоиде ABCD через точку пересечения диагоналей проведена прямая, перпендикулярная к одной из сторон. Доказать, что если эта прямая делит другую сторону пополам, то дельтоид можно вписать в окружность.

Пусто прямая NM пересекает сторонe BC под прямым углом, а сторону AD делит пополам. Тогда /EMB=/MEC=/NAE, а это значит, что утверждение доказано.

Утверждение: если четырехугольник является вписанным, то центр описанной около него окружности – точка пересечения серединных перпендикуляров к сторонам четырехугольника.

В самом деле, серединный перпендикуляр к отрезку содержит все точки, равно удаленные от концов этого отрезка, следовательно, точка пересечения серединных перпендикуляров вписанного в окружность четырехугольника, равно удалена от вершин этого четырехугольника, т.е. от некоторых точек окружности.

По определению центра окружности, из этого следует, что данная точка – центр описанной около этого четырехугольника окружности.

Вписанный дельтоид является примером гармонического четырехугольника (вписанный четырехугольник с перпендикулярными диагоналями, произведение длин противоположенных сторон которого равны)

Вписанный в окружность четырехугольник обладает рядом интереснейших свойств. Одно из них было доказано древнегреческим математиком и астрономом Клавдием Птолемеем (около 100 – 178 г. н. э.) в его знаменитом сочинении «Альмагест» (астрономы в странах арабского Востока называли эту книгу «Альмаджисти» — «Величайшие», отсюда и происходит её название «Альмагест»).

Теорема, носящая имя Птолемея: произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон.

Т.к. у дельтоида две пары равных соседних сторон, то утверждение выглядит так: d₁*d₂=2a*b

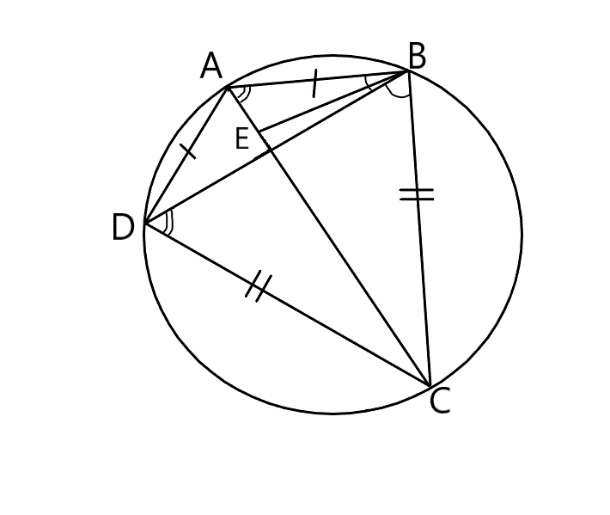
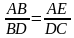
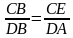
Возьмём на диагонали AC точку E так, что /ABE = /DBC. Тогда ∆ABE и ∆DBC подобны, т.к. /BAE = /BAC= /BDC. Поэтому , т.е. AB*DC = AE*DB. (1) Ясно также, что /CBE = /DBA (т.к. /CBE = /DBC + /DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. /BCE = /BDA (опираются на одну дугу), поэтому , то есть CB*DA = CE*DB (2). Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB = DB*(AE + CE) = BD*AC,

Сумма квадратов неравных сторон равна учетверённому квадрату радиуса описанной окружности.

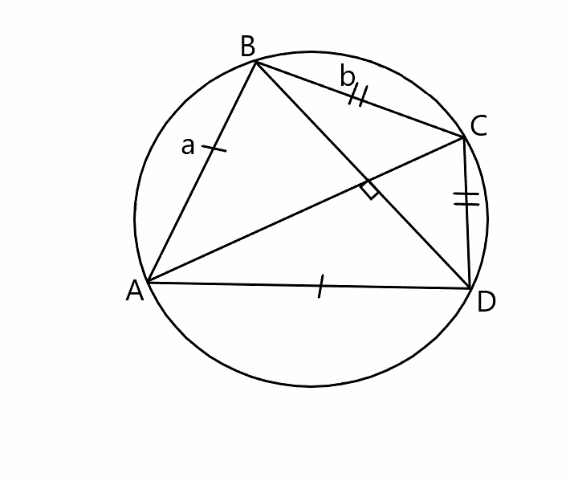
Рассмотрим вписанный в окружность четырехугольник ABCD, диагонали которого перпендикулярны. В нём AB=a, BC=b, CD=c, AD=a, а радиус описанной окружности равен R. Докажем, что

.

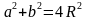
Обозначим BD как d_1, AC как d_2, /ABD как /1, /BAC как /2, /CAD как /3, /ADB как /4, тогда /BCA=/4 ( т.к. опирается с /ADB на одну дугу), аналогично /BCA=/4, /CBD=/3, /BDC=/2, /ACD=/1. По теореме синусов получаем:

a = 2R*sin /2, b = 2R*sin /1

(так как /2 = 90 ⸰ — /1), из этого

a 2 + b 2 = 4R 2 sin /1 + 4R 2 cos /1 = 4R 2 , следовательно, a 2 + b 2 = 4R 2

Примеры решения задач.

Выше мы рассмотрели общие свойства дельтоида. Также свойства некоторых особых видов таких четырехугольников.

Теперь решим несколько задач, в которых встречается данный четырехугольник.

В дельтоиде средние линии пересекаются на оси симметрии дельтоида.

Пусть K, L, M, N – середины сторон дельтоида. Поскольку KLMN – прямоугольник, то его диагонали пересекаются на оси симметрии BD.

В дельтоид вписана окружность, которая касается равных сторон в точках M и N, P и Q. Определить вид четырехугольника MNPQ.

Пусть ABCD — данный четырехугольник.

Поскольку BM=BN, то MN||AC. Аналогично QP||AC. Поскольку QM=NP, то четырехугольник – равнобедренная трапеция.

Построить дельтоид ABCD по сторонам a, b и углу между равными сторонами y.

Построить произвольную прямую.

Взять на ней точку D.

Отложить от точки в данную полуплоскость угол y.

Разделить угол пополам (т.к. у дельтоида диагональ является биссектрисой).

Провести Окр (D, a), которая пересечет стороны угла в точках A и C.

Провести Окр (A, b), которая пересечет биссектрису угла y в точке B.

ABCD — данный четырехугольник.

Т.к. диагональ AC делится точкой пересечения диагоналей пополам, то AO=1/2d

Из треугольника AOB:BO=

Из треугольника AOD:DO=

Т.к. S=12d1*d2 получаем S=12d1*( )

В данной работе было рассмотрено что такое дельтоид, какими свойствами должен обладать четырехугольник, чтобы его можно было назвать дельтоидом. В заключении работы было разобрано несколько задач.

Но это далеко не всё, что может быть изучено по теме «Дельтоид».

Если посмотреть на карту неба, то мы можем обнаружить знакомую нам фигуру. Четыре самые яркие образуют ромбоид – характерную геометрическую фигуру созвездия Весы. В окружающем мире дельтоид встречается в конструировании воздушных змеев и летательных аппаратов, плавательных судов, а также в области биологии: крона дерева туя, лист березы, тело рыбы, форма носа, соединенные пальцы человека и др.

В качестве направлений для дальнейших исследований проект предполагает рассмотреть свойства аналогичных фигур и в стереометрии.

Расширить представленную в проекте тему можно изучением применения свойств дельтоида в оригами (Оригами – наглядная модель евклидовой геометрии)

Список используемой литературы.

Журнал «Квант» №2, 1992 г. http://kvant.mccme.ru/1992/02/p37.htm

Журнал «Квант» №10, 1991 г. http://kvant.mccme.ru/1991/10/p48.htm

И.Л. Никольская «Факультативны курс математике 7-9».

В.В. Прасолов «Задачи по планиметрии».

И.Ф. Шарыгин «Геометрия (планиметрия) 7-9».

В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович «Практикум по элементарной математике (геометрия)».

📺 Видео

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Свойства дельтоида и антипараллельностьСкачать

Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

8 класс, 34 урок, Теорема о вписанном углеСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Хитрости в решении геометрических задач в ОГЭ по математике | Математика TutorOnlineСкачать

ВОТ ЭТО ПОВОРОТ! Такого вы точно не знали!Скачать

Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Вписанные и описанные окружности. Задание №16 | PARTA МАТЕМАТИКА ОГЭ 2023Скачать

ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать