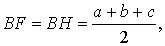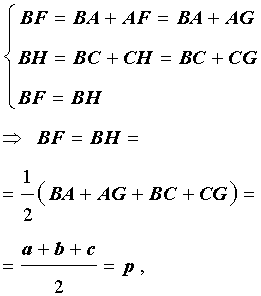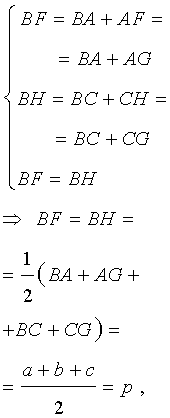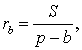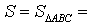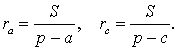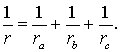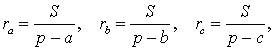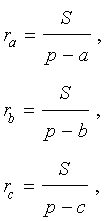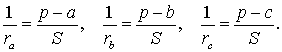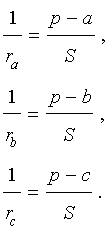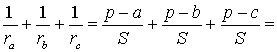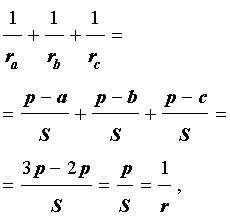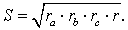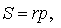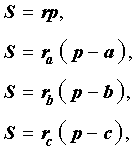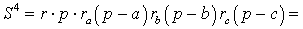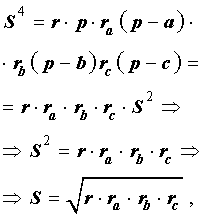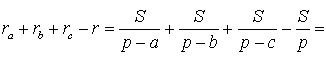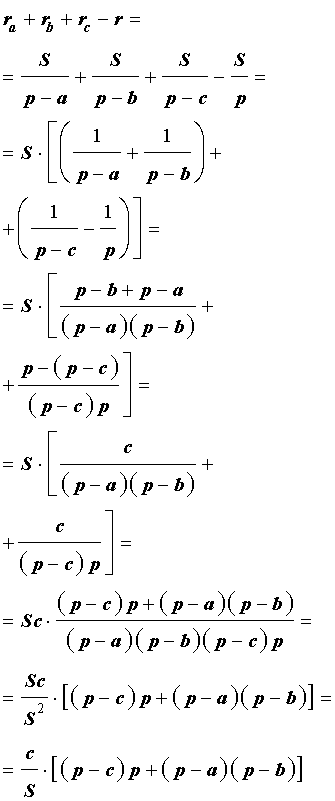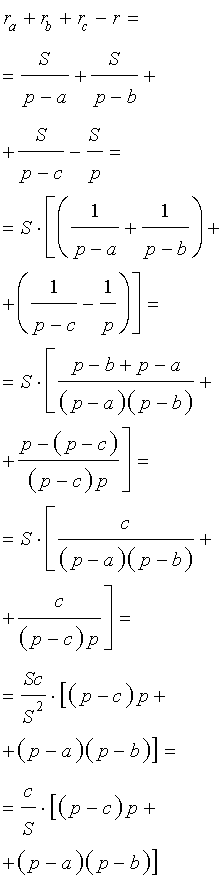Как найти расстояние между центрами вписанной и вневписанной окружностей (3 видео)

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

Треугольник
Выпуклый, правильный многоугольник
Квадрат
Равнобедренная трапеция
Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Содержание

Свойства вписанной окружности
В треугольник
В четырехугольник
Примеры вписанной окружности
Верные и неверные утверждения
Окружность вписанная в угол
Вневписанные окружности
МАТЕМАТИКА
🎦 Видео

Свойства вписанной окружности

В треугольник

В любой треугольник может быть вписана окружность, причем только один раз.
Центр вписанной окружности — точка пересечения биссектрис треугольника.
Вписанная окружность касается всех сторон треугольника.
Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

Не во всякий четырехугольник можно вписать окружность.
Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито).
Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
Точка пересечения биссектрис — это центр вписанной окружности.
Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника.
Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Треугольник
Четырехугольник
Многоугольник

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
Любой параллелограмм можно вписать в окружность. Неверное утверждение.
В любой четырехугольник можно вписать окружность. Неверное утверждение.
В любой ромб можно вписать окружность. Верное утверждение.
Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение.
Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение.
Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать

Вневписанные окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

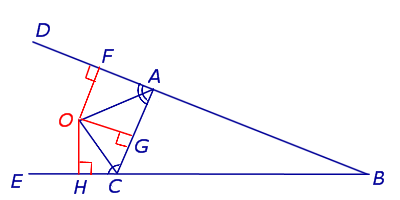
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

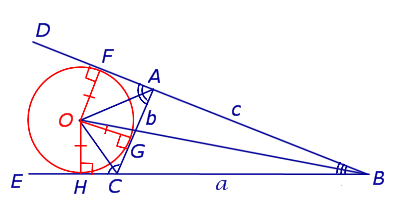
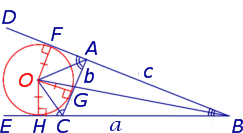
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать

МАТЕМАТИКА

Формула Эйлера

Мы знаем, что в каждый треугольник можно вписать окружность и можно описать около него окружность. Ясно, что вписанная окружность лежит внутри описанной, поскольку вписанная окружность лежит внутри треугольника, а сам треугольник лежит внутри описанной окружности.

Радиусы вписанной и описанной окружностей и расстояние между их центрами всегда связаны между собой определенным соотношением. Справедлива следующая теорема.

Теорема. В треугольнике радиус R описанной окружности и радиус r вписанной окружности связаны с расстоянием d между их центрами соотношением

В частности, если d=0 (центры окружностей совпадают), то .

Эта формула называется формулой Эйлера.

Доказательство.

Рассмотрим треугольник АВС, у которого точка О – центр описанной окружности, а точка – центр вписанной окружности. Будем считать пока, что (рисунок 1). Проведем биссектрисы и углов А и В. Они пересекаются с описанной окружностью в некоторых точках и . Пусть P и Q – точки пересечения прямой с описанной окружностью. По теореме о произведении отрезков пересекающихся хорд , или

Заметим теперь, что поскольку и – биссектрисы углов А и В, то , а . Следовательно,

Поэтому треугольник равнобедренный: . Таким образом, соотношение можно переписать так:

Проведем теперь диаметр описанной окружности и обозначим буквой К точку касания вписанной окружности и стороны АВ. Треугольники и подобны (они прямоугольные и имеют равные углы А и ), поэтому

Откуда . Подставив это выражение, получим

В случае d=0 (рисунок 2) каждая из сторон треугольника АВС равна , а значит, этот треугольник равносторонний.

Поэтому , , и, следовательно, . Теорема доказана.

Замечание. В ходе доказательства теоремы мы установили весьма полезный факт:

Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности.

Теорема Птолемея

В любой треугольник можно вписать окружность и около него можно описать окружность. Однако для других многоугольников это не так. Мы знаем, например, что в четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна . Эти утверждения очень похожи друг на друга. Используя скобки, их можно объединить в одно:

Описанная (вписанная) окружность для данного четырехугольника существует тогда и только тогда, когда суммы его противоположных углов (сторон) равны.

Существуют и другие характеристические свойства вписанных и описанных четырехугольников. Наиболее известное основано на теореме Птолемея.

Теорема (Птолемея). Произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных сторон.

Доказательство.

Рассмотрим вписанный четырехугольник АВСD. Для удобства введем обозначение: АВ = а, ВС = b, CD = c, DA = d, AC = m, BD = n (рисунок 3) и докажем, что .

На диагонали АС возьмем такую точку М, что . Треугольники АВМ и DBC подобны по двум углам ( по построению, а углы ВАМ и BDC равны как вписанные и опирающиеся на одну и ту же дугу). Следовательно, , откуда , или (1).

Далее, треугольники МВС и ADB также подобны, так как , а углы ВСМ и BDA равны как вписанные и опирающиеся на одну и ту же дугу. Поэтому , , откуда , или (2).

Сложив равенства (1) и (2), получим , или , что и требовалось доказать.

Оказывается, что рассмотренное свойство вписанного четырехугольника является характеристическим, то есть верно и обратное утверждение.

Если в выпуклом четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон, то около него можно описать окружность.

Рекомендую далее изучить тему «Вневписанные окружности».

Спасибо, что поделились статьей в социальных сетях

Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.