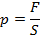Давление физика скаляр или вектор

ДАВЛЕНИЕ — скалярная величина, характеризующая напряжённое состояние сплошной среды. В случае равновесия произвольной и движения идеальной (лишённой внутр. трения) сред Д. равно взятой с обратным знаком величине нормального напряжения на произвольно ориентированной в данной точке площадке. Cp. величина Д. на к—л. площадку равна отношению ср. значения действующей перпендикулярно площадке силы к площади этой площадки. При движении среды, обладающей внутр. трением, под Д. понимают взятое с обратным знаком среднее арифметическое трех нормальных напряжений на взаимно перпендикулярных площадках в данной точке среды, представляющее в этом случае также скаляр — одну треть линейного инварианта тензора напряжений. Д., так же как плотность и темп-pa, представляет собой осн. макроскопич. параметр состояния жидкости и газа. Объяснение молекулярного механизма возникновения Д. см. в статьях Жидкость, Кинетическая теория газов.

Единицей измерения Д. в системе СИ является паскаль (1 Па=1 Н/м 2 =0,102 кгс/м 2 ). Допускается также применение следующих единиц: 1 кгс/см 2 =1 ат=9,81*10 4 Па; 1 атм=1,01*10 5 Па; 1 мм рт. ст. (1 торр)=133,322 Па.

Разности Д. измеряют манометрами, абсолютные Д., в частности атмосферное Д.,- барометрами; быстро меняющиеся Д.- разнообразными электрич. индукционными и ёмкостными датчиками.

Видео:Давление. Единицы давленияСкачать

Дав­ле­ние – ска­ляр­ная ве­ли­чи­на

Тема: Давление в жидкости и газе

Для на­ча­ла вспом­ним, что такое дав­ле­ние. Это фи­зи­че­ская ве­ли­чи­на, рав­ная мо­ду­лю силы , дей­ству­ю­щей пер­пен­ди­ку­ляр­но по­верх­но­сти, ко­то­рая при­хо­дит­ся на еди­ни­цу пло­ща­ди этой по­верх­но­сти.

Важно по­ни­мать, что дав­ле­ние – ве­ли­чи­на ска­ляр­ная, то есть у нее нет на­прав­ле­ния.

Дав­ле­ние – ска­ляр­ная ве­ли­чи­на

Если в сплош­ном бе­тоне сде­лать сфе­ри­че­скую по­лость и взо­рвать там порох, как будет рас­про­стра­нять­ся дав­ле­ние? Во все сто­ро­ны (см. рис. 4).

Рис. 4. Рас­про­стра­не­ние дав­ле­ния

Как будут раз­ле­тать­ся оскол­ки бе­тон­ной обо­лоч­ки – это будет за­ви­сеть от самой обо­лоч­ки, от того, какая она проч­ная, тол­стая. Но да­вить на стен­ки по­ло­сти газ будет везде оди­на­ко­во. И если бы внут­ри по­ло­сти был ка­кой-ни­будь пред­мет, на него газ тоже ока­зы­вал бы дав­ле­ние, при­чем со всех сто­рон (см. рис. 5), как бы мы ни по­вер­ну­ли этот пред­мет.

Рис. 5. Дав­ле­ние газа на пред­мет

Если мы за­хо­тим из­ме­рить дав­ле­ние, на­при­мер под водой, то на нуж­ную нам глу­би­ну необ­хо­ди­мо по­ме­стить ма­но­метр (см. рис. 6).

Рис. 6. Ма­но­метр

Это неболь­шая эла­стич­ная мем­бра­на, ко­то­рая про­ги­ба­ет­ся под дей­стви­ем дав­ле­ния. Как бы мы ни рас­по­ло­жи­ли эту мем­бра­ну – го­ри­зон­таль­но, вер­ти­каль­но, наи­ско­сок, на нее все­гда будет дей­ство­вать одна и та же сила и мем­бра­на про­гнет­ся оди­на­ко­во.

То есть для дав­ле­ния на­прав­ле­ние не имеет смыс­ла. Оно про­сто есть в дан­ной точке, как и тем­пе­ра­ту­ра. Тем­пе­ра­ту­ра тоже не имеет на­прав­ле­ния. Она ни­ку­да не на­прав­ле­на, она ха­рак­те­ри­зу­ет энер­гию теп­ло­во­го дви­же­ния ча­стиц ве­ще­ства. В дан­ной точке тем­пе­ра­ту­ра имеет опре­де­лен­ное зна­че­ние. Для век­тор­ной ве­ли­чи­ны, на­при­мер силы, мы можем за­дать во­прос: «Куда она дей­ству­ет, в каком на­прав­ле­нии?» (см. рис. 7).

Рис. 7. Век­тор­ная ве­ли­чи­на

Для дав­ле­ния и тем­пе­ра­ту­ры этот во­прос про­сто не имеет смыс­ла.

Дав­ле­ние пе­ре­да­ет­ся ве­ще­ством из одной точки в дру­гую. Вода в гид­рав­ли­че­ском прес­се пе­ре­да­ла дав­ле­ние. Когда мы на­ка­чи­ва­ем ко­ле­со на ве­ло­си­пе­де, мы давим на пор­шень на­со­са и дав­ле­ние по­вы­ша­ет­ся в ко­ле­се (см. рис. 8).

Рис. 8. Уве­ли­че­ние дав­ле­ния в ко­ле­се

Если два че­ло­ве­ка возь­мут­ся за про­дол­го­ва­тый воз­душ­ный шарик и один из них со­жмет этот шарик, вто­рой это по­чув­ству­ет, дав­ле­ние во всем ша­ри­ке по­вы­сит­ся (см. рис. 9).

Воз­дух тоже пе­ре­да­ет дав­ле­ние. А если мы так же со­жмем ме­тал­ли­че­ский прут, пе­ре­да­чу дав­ле­ния мы не ощу­тим. Вы­хо­дит, твер­дые тела не пе­ре­да­ют дав­ле­ние? Если по этому же пруту уда­рить (см. рис. 10), то он за­зве­нит весь, звук по пруту пе­ре­даст­ся. А зву­ко­вая волна – это об­ласть по­вы­шен­но­го дав­ле­ния, ко­то­рая пе­ре­ме­ща­ет­ся.

Рис. 9. По­вы­ше­ние дав­ле­ния в ша­ри­ке

Рис. 10. Удар по же­лез­но­му пруту

С твер­ды­ми те­ла­ми, как ви­ди­те, всё слож­нее, эти про­цес­сы изу­ча­ет наука «ме­ха­ни­ка сплош­ных сред».

Воз­дух тоже не все­гда пе­ре­да­ет дав­ле­ние: если над Аме­ри­кой про­мчал­ся ура­ган (см. рис. 11) и там об­ласть по­вы­шен­но­го дав­ле­ния, то в Рос­сии мы этого не по­чув­ству­ем.

Рис. 11. При­род­ных яв­ле­ний в Аме­ри­ке мы не по­чув­ству­ем

1. Как сила тяжести действует на жидкости и газы?

Все тела со­сто­ят из мо­ле­кул. И жид­ко­сти тоже. На все тела на Земле дей­ству­ет сила тя­же­сти. Мо­ле­ку­лы жид­ко­сти при­тя­ги­ва­ют­ся к земле. Мо­ле­ку­лы верх­них слоев вслед­ствие сво­е­го при­тя­же­ния к Земле дей­ству­ют своим весом на мо­ле­ку­лы по­сле­ду­ю­щих слоев (Рис. 1).

Рис. 1. Мо­ле­ку­лы верх­них слоев жид­ко­сти и газа своим весом дей­ству­ют на мо­ле­ку­лы ниж­них слоев

Таким об­ра­зом, со­зда­ет­ся дав­ле­ние. По за­ко­ну Пас­ка­ля оно пе­ре­да­ет­ся во всех на­прав­ле­ни­ях. Убе­дить­ся в этом можно на опыте.

2. Доказательство существования давления в жидкости

Возь­мем труб­ку. С одной сто­ро­ны она от­кры­та, с дру­гой сто­ро­ны ее за­тя­ну­ли ре­зи­но­вой плен­кой.

Рис. 2. Труб­ка для изу­че­ния дав­ле­ния в жид­ко­сти

Сей­час уро­вень этой плен­ки вро­вень с тор­цом труб­ки. Но если на­лить в труб­ку неко­то­рое ко­ли­че­ство жид­ко­сти, то мы уви­дим, что плен­ка про­гну­лась.

Если те­перь взять сосуд с жид­ко­стью и по­гру­зить труб­ку вер­ти­каль­но в сосуд, то можно убе­дить­ся, что дав­ле­ние внут­ри жид­ко­сти, на­хо­дя­щей­ся в этом со­су­де, дей­стви­тель­но су­ще­ству­ет.

Будем по­сте­пен­но по­гру­жать труб­ку в жид­кость и на­блю­дать за плен­кой на ниж­нем конце труб­ки. Можно ви­деть, что про­гиб плен­ки умень­ша­ет­ся по мере по­гру­же­ния труб­ки в жид­кость. А когда уро­вень жид­ко­сти в труб­ке и в со­су­де ста­нут оди­на­ко­вы­ми, про­гиб плен­ки пол­но­стью ис­чез­нет (Рис. 3).

Рис. 3. По про­ги­бу ре­зи­но­вой плен­ки можно су­дить об из­ме­не­нии дав­ле­ния в жид­ко­сти с глу­би­ной

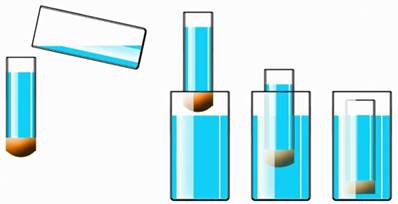
Это го­во­рит о том, что внут­ри жид­ко­сти су­ще­ству­ет дав­ле­ние, и оно ме­ня­ет­ся с глу­би­ной. Чем глуб­же мы по­гру­жа­ем­ся в жид­кость, тем дав­ле­ние жид­ко­сти ста­но­вит­ся боль­ше. Такое дав­ле­ние на­зы­ва­ет­ся гид­ро­ста­ти­че­ским, так как со­зда­ет­ся непо­движ­ной жид­ко­стью (от гре­че­ских слов hydor – вода, statos – непо­движ­ный).

3. Существует ли подобное давление в газах?

Мо­ле­ку­лы газов также при­тя­ги­ва­ют­ся к Земле, по­это­му дав­ле­ние, по­доб­ное гид­ро­ста­ти­че­ско­му дав­ле­нию жид­ко­стей, без­услов­но, су­ще­ству­ет. Толь­ко необ­хо­ди­мо пом­нить, что плот­ность газов зна­чи­тель­но мень­ше, чем плот­ность жид­ко­стей. И по­это­му, при про­чих рав­ных усло­ви­ях, дав­ле­ние газа во много раз мень­ше, чем дав­ле­ние жид­ко­стей.

Итак, бла­го­да­ря при­тя­же­нию к Земле, внут­ри жид­ко­стей и газов су­ще­ству­ет дав­ле­ние. А от каких па­ра­мет­ров за­ви­сит это дав­ле­ние, вы узна­е­те на сле­ду­ю­щих уро­ках.

В.В.Белага, И.А.Ломаченков, Ю.А.Панибратцев «Физика», Москва, Просвещение, 2016 31, с.78-79 читать.

Видео:Скалярные и векторные величины, основные определения.Скачать

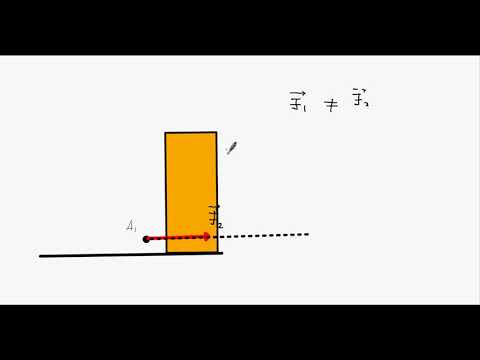
Векторная величина в физике: определение, обозначение, примеры

В математике вектор — это направленный отрезок определенной длины. В физике под векторной величиной понимают полную характеристику некоторой физической величины, которая обладает модулем и направлением действия. Рассмотрим основные свойства векторов, а также примеры физических величин, которые являются векторными.

Видео:Давление. Единицы давления | Физика 7 класс #25 | ИнфоурокСкачать

Скаляры и вектора

Скалярные величины в физике являются параметрами, которые могут быть измерены и представлены одним числом. Например, температура, масса и объем являются скалярами, поскольку они измеряются числом градусов, килограмм и кубических метров соответственно.

В большинстве же случаев оказывается, что число, определяющее скалярную величину, не несет исчерпывающей информации. Например, рассматривая такую физическую характеристику, как ускорение, будет недостаточно сказать, что оно равно 5 м/с 2 , поскольку нужно знать, куда оно направлено, против скорости движения тела, под некоторым углом к этой скорости или иначе. Помимо ускорения, примером векторной величины в физике является скорость. Также в эту категорию входят сила, напряженность электрического поля и многое другие.

Согласно определению векторной величины как направленного в пространстве отрезка, она может быть представлена в виде набора чисел (компонент вектора), если ее рассматривать в определенной системе координат. Чаще всего в физике и математике возникают задачи, которые для описания вектора требуют знания его двух (задачи на плоскости) или трех (задачи в пространстве) компонентов.

Видео:Урок 42 (осн). Давление. Единицы давленияСкачать

Определение вектора в n-мерном пространстве

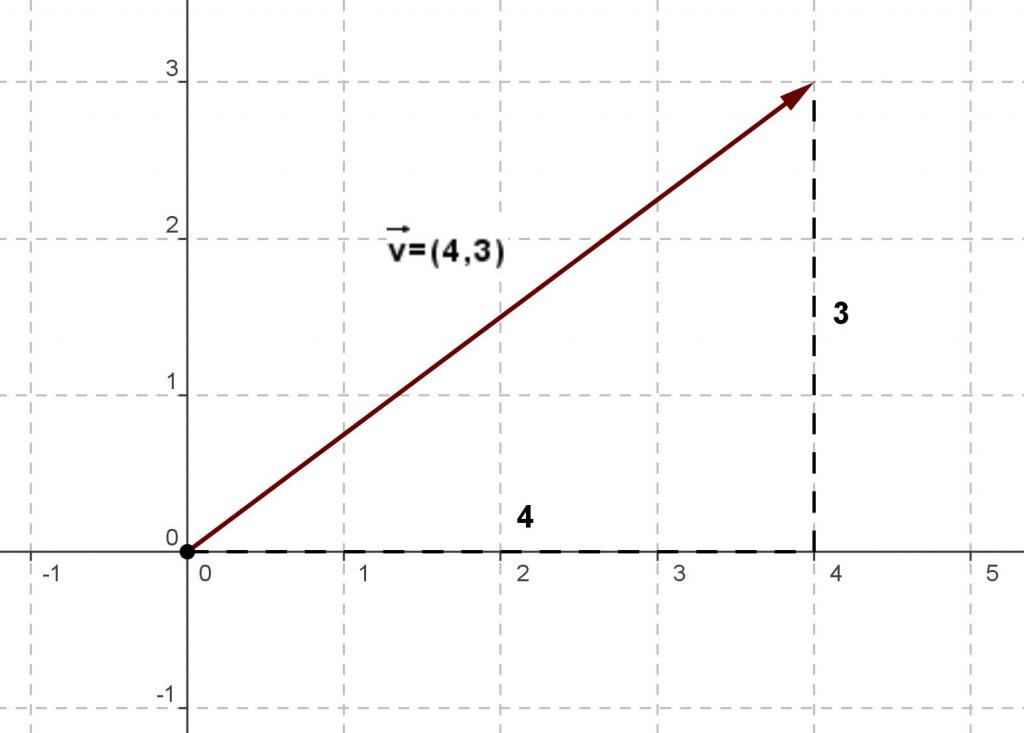
В n-мерном пространстве, где n — целое число, вектор будет однозначно определен, если известны его n компонент. Каждая компонента представляет собой координату конца вектора вдоль соответствующей оси координат при условии, что начало вектора находится в начале системы координат n-мерного пространства. В итоге вектор может быть представлен так: v = <a₁, a₂, a₃, . a_n>, где a₁ — скалярное значение 1-й компоненты вектора v. Соответственно, в 3-х мерном пространстве вектор запишется как v = <a₁, a₂, a₃>, а в 2-х мерном — v = <a₁, a₂>.

Как обозначается векторная величина? Любой вектор в 1-мерном, 2-мерном и 3-мерном пространствах можно представить как направленный отрезок, лежащий между точками A и B. В этом случае он обозначается как AB → , где стрелка показывает, что речь идет о векторной величине. Последовательность букв принято указывать от начала вектора к его концу. Это означает, что если координаты точек A и B, например, в 3-мерном пространстве, равны <x₁, y₁, z₁> и <x₂, y₂, z₂> соответственно, тогда компоненты вектора AB → будут равны <x₂-x₁, y₂-y₁, z₂-z₁>.

Видео:Физика | Ликбез по векторамСкачать

Графическое представление вектора

На рисунках принято изображать векторную величину в виде отрезка, на его конце имеется стрелочка, указывающая направление действия физической величины, представлением которой она является. Этот отрезок обычно подписывают, например, v → или F → , чтобы было понятно, о какой характеристике идет речь.

Графическое представление вектора помогает понять, куда приложена и в каком направлении действует физическая величина. Кроме того, многие математические операции над векторами удобно совершать, используя их изображения.

Видео:Физика 7 класс. §35 Давление. Единцы давленияСкачать

Математические операции над векторами

Векторные величины, так же как и обычные числа, можно складывать, вычитать и умножать как друг с другом, так и с другими числами.

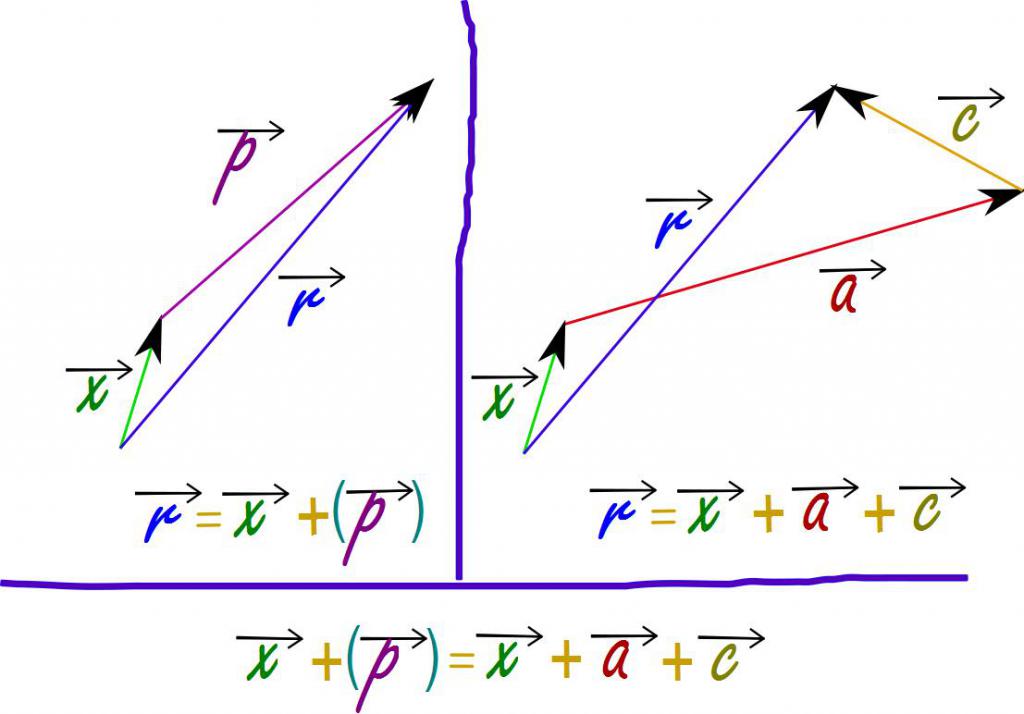
Под суммой двух векторов понимают третий вектор, который получается, если суммируемые параметры расположить так, чтобы конец первого совпадал с началом второго вектора, а затем, соединить начало первого и конец второго. Для выполнения этого математического действия разработаны три основных метода:

1. Метод параллелограмма, заключающийся в построении геометрической фигуры на двух векторах, которые выходят из одной и той же точки пространства. Диагональ этого параллелограмма, которая выходит из общей точки начала векторов, будет являться их суммой.
2. Метод многоугольника, суть которого состоит в том, что начало каждого последующего вектора следует располагать в конце предыдущего, тогда суммарный вектор будет соединять начало первого и конец последнего.
3. Аналитический метод, который состоит в попарном сложении соответствующих компонент известных векторов.

Что касается разницы векторных величин, то ее можно заменить сложением первого параметра с тем, который противоположен по направлению второму.

Умножение вектора на некоторое число A выполняется по простому правилу: на это число следует умножить каждую компоненту вектора. В результате получается также вектор, модуль которого в A раз больше исходного, а направление либо совпадает, либо противоположно исходному, все зависит от знака числа A.

Делить вектор или число на него нельзя, а вот деление вектора на число A аналогично умножению на число 1/A.

Видео:Физика.7 класс. Скалярные и векторные физические величины /11.09.2020/Скачать

Скалярное и векторное произведения

Умножение векторов можно выполнять двумя различными способами: скалярно и векторно.

Скалярным произведением векторных величин называется такой способ их умножения, результатом которого является одно число, то есть скаляр. В матричном виде скалярное произведение записывается как строки компонента 1-го вектора на столбец компонент 2-го. В итоге в n-мерном пространстве получается формула: (A → *B → ) = a₁*b₁+a₂*b₂+. +a_n*b_n.

В 3-мерном пространстве можно определить скалярное произведение иначе. Для этого нужно умножить модули соответствующих векторов на косинус угла между ними, то есть (A → *B → ) = |A → |*|B → |*cos(θ_AB). Из этой формулы следует, что если вектора направлены в одном направлении, то скалярное произведение равно умножению их модулей, а если вектора перпендикулярны друг другу, тогда оно оказывается равным нулю. Отметим, что модуль вектора в прямоугольной системе координат определяется как квадратный корень от суммы квадратов компонент этого вектора.

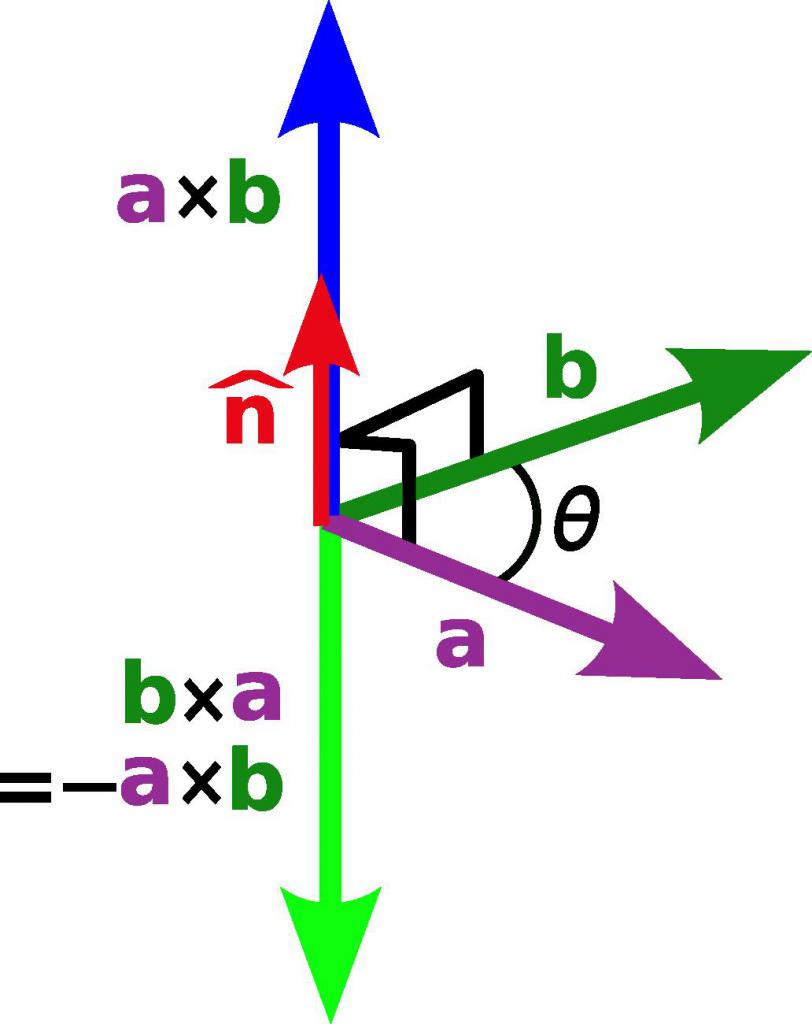
Под векторным произведением понимают такое умножение вектора на вектор, результатом которого также является вектор. Его направление оказывается перпендикулярно каждому из умножаемых параметров, а длина равна произведению модулей векторов на синус угла между ними, то есть A → x B → = |A → |*|B → |*sin(θ_AB), где значок «x» обозначает векторное произведение. В матричном виде этот вид произведения представляется как определитель, строками которого являются элементарные вектора данной системы координат и компоненты каждого вектора.

Как скалярное, так и векторное произведения используют в математике и физике для определения многих величин, например, площади и объема фигур.

Далее в статье приводятся примеры векторных величин в физике.

Видео:Физика. Объяснение темы "Векторные и скалярные величины"Скачать

Скорость и ускорение

Под скоростью в физике понимают быстроту изменения местоположения данной материальной точки. Измеряется скорость в системе СИ в метрах в секунду (м/с), а обозначается символом v → . Под ускорением понимают быстроту изменения скорости. Ускорение измеряется в метрах в квадратную секунду (м/с 2 ), а обозначается обычно символом a → . Значение 1 м/с 2 говорит о том, что за каждую секунду тело увеличивает свою скорость на 1 м/с.

Скорость и ускорение — это векторные величины, которые участвуют в формулах второго закона Ньютона и перемещения тела как материальной точки. Скорость всегда направлена вдоль направления движения, ускорение же может быть направлено произвольным образом относительно движущегося тела.

Видео:ДАВЛЕНИЕ физика 7 класс ЕДИНИЦЫ ДАВЛЕНИЯ ПерышкинСкачать

Физическая величина сила

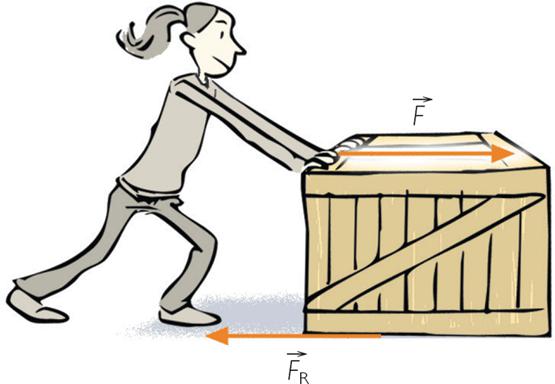
Сила — векторная физическая величина, которая отражает интенсивность взаимодействия между телами. Обозначается она символом F → , измеряется в ньютонах (Н). По определению, 1 Н — это сила, способная за каждую секунду времени изменять скорость тела, имеющего массу 1 кг, на 1 м/с.

Эта физическая величина широко применяется в физике, поскольку с ней связаны энергетические характеристики процессов взаимодействия. Природа силы может быть самой разной, например, гравитационные силы планет, сила, которая заставляет двигаться автомобиль, упругие силы твердых сред, электрические силы, описывающие поведение электрических зарядов, магнитные, ядерные силы, которые обуславливают стабильность атомных ядер, и так далее.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Векторная величина давление

С понятием силы тесно связана другая величина — давление. Под ним в физике понимают нормальную проекцию силы на площадку, на которую она действует. Поскольку сила является вектором, то, согласно правилу умножения числа на вектор, давление также будет векторной величиной: P → = F → /S, где S — площадь. Давление измеряется в паскалях (Па), 1 Па — это параметр, при котором перпендикулярная сила в 1 Н действует на поверхность площадью 1 м 2 . Исходя из определения, вектор давления направлен в том же направлении, что и вектор силы.

В физике понятие давления часто используется при изучении явлений в жидкостях и газах (например, закон Паскаля или уравнение состояния идеального газа). Давление тесно связано с температурой тела, поскольку кинетическая энергия атомов и молекул, представлением которой является температура, объясняет природу существования самого давления.

Видео:Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Напряженность электрического поля

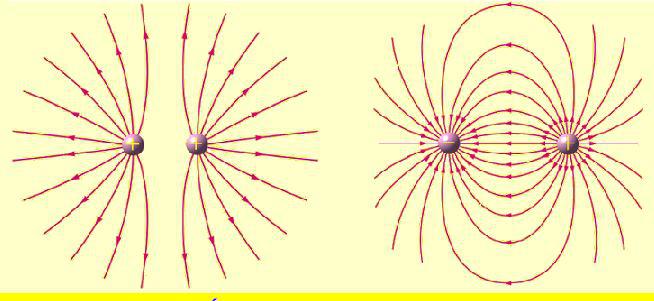
Вокруг любого заряженного тела существует электрическое поле, силовой характеристикой которого является его напряженность. Определяется эта напряженность как сила, действующая в данной точке электрического поля на единичный заряд, помещенный в эту точку. Обозначается напряженность электрического поля буквой E → и измеряется в ньютонах на кулон (Н/Кл). Вектор напряженности направлен вдоль силовой линии электрического поля в ее направлении, если заряд положительный, и против нее, если заряд отрицательный.

Напряженность электрического поля, создаваемого точечным зарядом, можно определить в любой точке, используя закон Кулона.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Магнитная индукция

Магнитное поле, как показали в XIX веке ученые Максвелл и Фарадей, тесно связано с электрическим полем. Так, изменяющееся электрическое поле порождает магнитное, и наоборот. Поэтому оба вида полей описываются в рамках электромагнитных физических явлений.

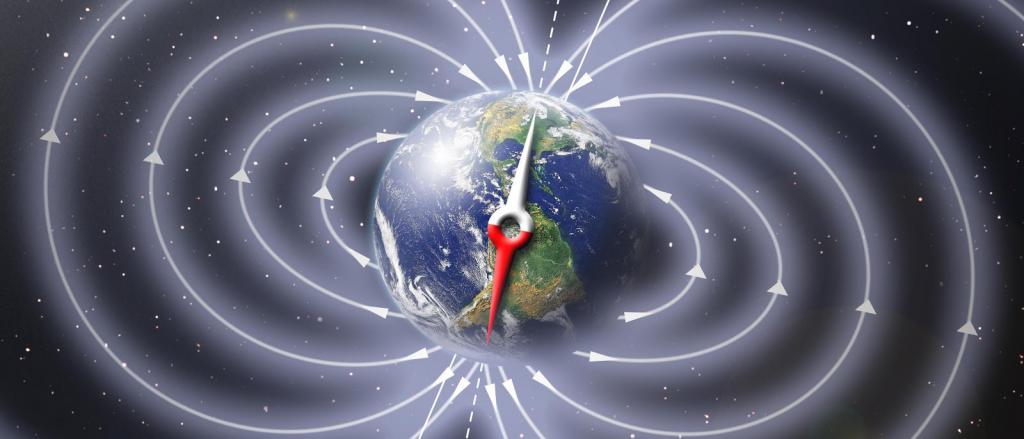
Магнитная индукция описывает силовые свойства магнитного поля. Магнитная индукция — величина скалярная или векторная? Понять это можно, зная, что она определяется через силу F → , действующую на заряд q, который пролетает со скоростью v → в магнитном поле, согласно следующей формуле: F → = q*|v → x B → |, где B → — магнитная индукция. Таким образом, отвечая на вопрос, величина скалярная или векторная — магнитная индукция, можно сказать, что это вектор, который направлен от северного магнитного полюса к южному. Измеряется B → в теслах (Тл).

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Физическая величина кандела

Еще одним примером векторной величины является кандела, которая вводится в физику через световой поток, измеряемый в люменах, проходящий через поверхность, ограниченную углом в 1 стерадиан. Кандела отражает яркость света, поскольку показывает плотность светового потока.

🔥 Видео

Что такое давление?Скачать

Урок 53 (осн). Атмосферное давлениеСкачать

Что Такое Давление? Формула Давления. Физика 7 Класс. Простыми СловамиСкачать

Физика 7 класс. §36 Способы уменьшения и увеличения давленияСкачать

§ 35. Давление. Единицы давления.Скачать

Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

Физика 7 класс. ДавлениеСкачать