Даны векторы найти np

Этот онлайн калькулятор позволит вам очень просто найти проекцию одного вектора на другой вектор.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление проекции вектора на вектор и закрепить пройденный материал.

Калькулятор для вычисления проекции вектора на другой вектор

Инструкция использования калькулятора для вычисления проекции вектора на другой вектор

Ввод даных в калькулятор для вычисления проекции вектора на другой вектор

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления проекции вектора на другой вектор

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Теория. Проекция вектора на вектор

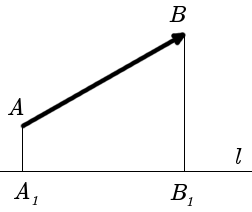
Определение Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b. Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора

При умножении вектора на число все его координаты

Умножаются на это число, при сложении векторов складываются их соответствующие координаты.

Координаты коллинеарных векторов пропорциональны.

Если A || B, то . Отсюда:

Ответ: .

Найти направляющие косинусы вектора А = .

Направляющие косинусы являются координатами орта (единичного вектора) данного направления.

Найдем модуль вектора А:

Разделив все координаты вектора А на его модуль, получим координаты орта:

Ответ:

Тогда AA + BB + GC = <2A + B— 3G; —A + B+ G; 3A — B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:

Для векторов A = , B = , C = , D = найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.

C = линейно зависимой или линейно независимой.

Система векторов называется линейно независимой, если равенство

Вычислим главный определитель Δ системы уравнений

По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).

Поскольку других решений нет, данная система векторов линейно независима.

Ответ: Система векторов линейно независима.

Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.

При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Найдем координаты этих векторов:

Из последней пропорции получаем, что Z = 1 – 2Y. Тогда

Но при этих значениях неизвестных

Условие задачи выполнено.

Используйте определение скалярного произведения:

Используем свойства скалярного произведения:

По определению скалярного произведения

Сложим левые и правые части полученных равенств:

Даны векторы А = и B = . Найти скалярное произведение

Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.

Используем свойства скалярного произведения:

Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.

Ответ: .

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.

Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Ответ: K = .

Найти проекцию вектора А = на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.

Используйте свойство направляющих косинусов:

Найдем cosγ: cos260o + cos245o + cos2γ = 1,

Тогда проекция А на заданную ось равна:

Работа с векторами в Python с помощью NumPy

В этом уроке мы узнаем, как создать вектор с помощью библиотеки Numpy в Python. Мы также рассмотрим основные операции с векторами, такие как сложение, вычитание, деление и умножение двух векторов, векторное точечное произведение и векторное скалярное произведение.

Что такое вектор в Python?

Вектор известен как одномерный массив. Вектор в Python – это единственный одномерный массив списков, который ведет себя так же, как список Python. Согласно Google, вектор представляет направление, а также величину; особенно он определяет положение одной точки в пространстве относительно другой.

Векторы очень важны в машинном обучении, потому что у них есть величина, а также особенности направления. Давайте разберемся, как мы можем создать вектор на Python.

Создание вектора в Python

Модуль Python Numpy предоставляет метод numpy.array(), который создает одномерный массив, то есть вектор. Вектор может быть горизонтальным или вертикальным.

Вышеупомянутый метод принимает список в качестве аргумента и возвращает numpy.ndarray.

Давайте разберемся в следующих примерах.

Пример – 1: горизонтальный вектор

Пример – 2: Вертикальный вектор

Базовые операции вектора Python

После создания вектора мы теперь будем выполнять арифметические операции над векторами.

Ниже приведен список основных операций, которые мы можем производить с векторами:

• сложение;
• вычитание;
• умножение;
• деление;
• точечное произведение;
• скалярные умножения.

Сложение двух векторов

В векторном сложении это происходит поэлементно, что означает, что сложение будет происходить поэлементно, а длина будет такой же, как у двух аддитивных векторов.

Давайте разберемся в следующем примере.

Вычитание

Вычитание векторов выполняется так же, как и сложение, оно следует поэлементному подходу, и элементы вектора 2 будут вычтены из вектора 1. Давайте разберемся в следующем примере.

Умножение векторов

Элементы вектора 1 умножаются на вектор 2 и возвращают векторы той же длины, что и векторы умножения.

Умножение производится следующим образом.

Первый элемент вектора 1 умножается на первый элемент соответствующего вектора 2 и так далее.

Операция деления двух векторов

В операции деления результирующий вектор содержит значение частного, полученное при делении двух элементов вектора.

Давайте разберемся в следующем примере.

Как видно из вышеприведенного вывода, операция деления вернула частное значение элементов.

Векторное точечное произведение

Векторное скалярное произведение выполняется между двумя последовательными векторами одинаковой длины и возвращает единичное скалярное произведение. Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.

Давайте разберемся в следующем примере.

Векторно-скалярное умножение

В операции скалярного умножения; мы умножаем скаляр на каждую компоненту вектора. Давайте разберемся в следующем примере.

В приведенном выше коде скалярное значение умножается на каждый элемент вектора в порядке s * v =(s * v1, s * v2, s * v3).