Даны прямая а и точка а не лежащая на прямой а сколько существует прямых параллельных

Геометрия | 5 — 9 классы

Даны прямая а и точка А, не лежащая на ней.

С помощью циркуля и линейки через точку А проведите прямую, параллельную прямой а.

Из точки О, лежащей на прямой а, провести окружность радисом ОА.

Она персечет прямую в точах О1 и О2.

Из точки О1 проведем окружность радиусом ОА, она пересечт первую окружность в точке А1.

Через точки Аи А1 проведем прямую паралльную прямой а А1 А

Видео:№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

Через точку, не лежащую на прямой, можно провести : 1) две прямые, параллельные данной прямой ; 2) только одну прямую, параллельную данной ; 3) ни одной прямой, параллельной данной ; 4) множество пара?

Через точку, не лежащую на прямой, можно провести : 1) две прямые, параллельные данной прямой ; 2) только одну прямую, параллельную данной ; 3) ни одной прямой, параллельной данной ; 4) множество параллельных прямых.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Докажите что через данную точку не лежащую на данной прямой проходит прямая параллельная данной?

Докажите что через данную точку не лежащую на данной прямой проходит прямая параллельная данной.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Через точку не лежащую на прямой, можно провести прямую, параллельно этой прямой?

Через точку не лежащую на прямой, можно провести прямую, параллельно этой прямой?

Видео:№197. Через точку, не лежащую на прямой р, проведены четыре прямые. Сколько из этих прямыхСкачать

Постройте с помощью циркуля и линейки 3 параллельных прямых к одной прямой?

Постройте с помощью циркуля и линейки 3 параллельных прямых к одной прямой.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Построение прямой проходящей через данную точку и перпендикулярной к данной прямой с помощью циркуля и линейки?

Построение прямой проходящей через данную точку и перпендикулярной к данной прямой с помощью циркуля и линейки.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Как провести перпендикуляр к прямой от точки, не лежащей на этой прямой, при помощи циркуля?

Как провести перпендикуляр к прямой от точки, не лежащей на этой прямой, при помощи циркуля?

Видео:№149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой a такСкачать

Проведите прямую?

Отметьте какую — нибудь точку А, лежащую на прямой, и точку В, не лежащую на прямой.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

С помощью циркуля и линейки постройте перпендикуляр к данной прямой через данную точку, лежащую вне этой прямой?

С помощью циркуля и линейки постройте перпендикуляр к данной прямой через данную точку, лежащую вне этой прямой.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Даны три точки , не лежащие на одной прямой?

Даны три точки , не лежащие на одной прямой.

Через каждые две точки проведена прямая.

Сколько прямых можно провести?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Дана прямая А и точка К, не лежащая на ней?

Дана прямая А и точка К, не лежащая на ней.

Через точку K проведены 4 прямые.

Сколько прямых пересекают a?

Вы зашли на страницу вопроса Даны прямая а и точка А, не лежащая на ней?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Вроде если не ошибаюсь, то 5 см.

1)угол А = 180° — 150° = 30°(из определения внешнего угла тр — ка) ; 2)угол В = 90° — 30° = 60° ( сумма острых углов прямоугольного тр — ка 90°) ; 3) т. К. ВВ1 — биссектриса, то угол АВВ1 = В1ВС = 60 : 2 = 30° и треугольник АВВ1 — равнобедренный : В..

Cos²A = 1 — sin²A = 1 — 0. 6² = 0. 64, cosA = 0. 8. tgA = sinA / cosA = 0. 6 / 0. 8 = 0. 75. В треугольнике АСН СН = АН·tgA = 8·0. 75 = 6. CН² = АН·ВН⇒ ВН = СН² / АН = 6² / 8 = 4. 5 — это ответ.

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

С какого языка тебе надо.

Амулет (с киргизского).

АС равно половине гипотенузы(5 см) сторона лежащая на против угла 90 градусов равна половине гипотенузы по теореме Пифагора : АВ вквадрате = АС в квадрате + СВ в кводрате 10 * 10 = 5 * 5 + СВ * СВ СВ квадрат = 100 — 25 СВ квадрат = 75 СВ = корень из7..

R = 2S / P. Периметр равен 50 см, площадь вычисляем по формуле Герона. Р = 50 / 2 = 25. S = √(25 * (25 — 17)(25 — 17)(25 — 16) = √(25 * 8 * 8 * 9) = √8 * 5 * 3 = 120 r = 2 * 120 / 50 = 24 / 5 = 4. 8 cм.

Какой конкретно угол? Если K, то 180° — (48° + 102°) = 30° Если 1, то 102 : 2 = 51° (соседний также находится) Если 2, сначала находим K, потом 1, далее 180° — (30° + 51°) = 99° Если 3, то находим сначала угол, смежный с 1 (они равны, так как поделе..

Видео:10 класс, 2 урок, Аксиомы стереометрииСкачать

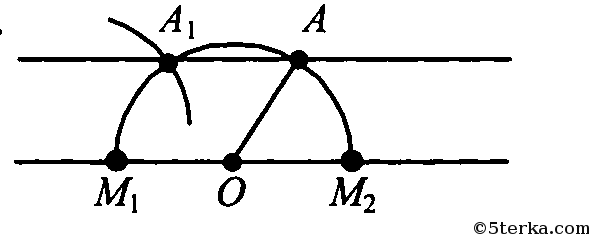
222 Даны прямая а и точка А, не лежащая на ней. С помощью циркуля и линейки через точку А проведите прямую, параллельную прямой а.

1. Построим окружность с центром в О ∈ а и радиусом ОА. Окружность пересечет прямую а в точках M₁ и М₂.

2. Построим окружность с центром в точке М₁ и радиусом ОА. Она пересечет первую окружность в точке А₁.

3. Проведем через точки А и А₁ прямую. АА₁ || а.

Решебник по геометрии за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №222
к главе «Глава III. Параллельные прямые. §2 Аксиома параллельных прямых».

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Стереометрия. Страница 2

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

1. Параллельность прямых в пространстве

Теорема. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Доказательство. Пусть b данная прямая и точка А, не лежащая на данной прямой. Проведем через точку А и прямую b плоскость α. А через точку А прямую a, параллельную прямой b. (Рис.1)

Допустим, что существует другая прямая а’, параллельная прямой b и проходящая через точку А. Тогда через них можно провести плоскость β. Отсюда следует, что через точку А и прямую b можно провести две плоскости. А это невозможно согласно теореме о единственности существования плоскости, проведеной через прямую и не лежащую на ней точку. Таким образом, плоскости α и β совпадают. А следовательно, согласно аксиоме, прямые а и a’ совпадают также.

5. Пример 1

Докажите, что если прямые АВ и CD скрещивающиеся, то прямые АС и BD тоже скрещиваются.

Доказательство:

Пусть даны две скрещивающиеся прямые АВ и CD. Проведем через прямую АВ и точку С плоскость α (Рис.5). Так как прямые АВ и CD скрещивающиеся, то прямая CD не лежит в плоскости α, а пересекает ее в одной точке С.

Отсюда следует, что точка D не принадлежит плоскости α. Она лежит вне ее.

Таким образом, если мы проведем прямую АС, то она полностью будет принадлежать плоскости α, так как две ее точки А и С принадлежат плоскости α.

А прямая BD не будет принадлежать плоскости α, так как точка D не принадлежит плоскости α. Прямая BD будет пересекать плоскость α в одной точке В.

Отсюда можно сделать вывод, что прямая АС не может пересекать прямую BD, так как прямая АС полностью принадлежит плоскости α. А прямая BD имеет только одну общую точку с плоскостью α, точку В. Но так как точка В не лежит на прямой АС, следовательно, прямые АС и BD не пересекаются. Они являются скрещивающимися.

Рис.5 Задача. Докажите, что если прямые АВ и CD скрещивающиеся.

Пример 2

Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем плоскость α через точки A, D, C и плосксоть α’ через точки А, В, С (Рис.6). Точки P, S, F, E являются серединами отрезков AB, BC, AD и CD соответственно. Необходимо доказать, что прямая PS параллельна прямой FE.

Рассмотрим треугольник АВС. Он полностью лежит в плоскости α’, так как три его вершины лежат в данной плоскости по построению. Отрезок PS представляет собой среднюю линию треугольника, которая параллельна АС.

Теперь рассмотрим треугольник АСD. Он полностью лежит в плоскости α, так как три его вершины лежат в данной плоскости по построению. Отрезок FE представляет собой среднюю линию треугольника, которая также параллельна АС.

Отсюда можно сделать вывод: если две прямые PS и FE параллельны третьей прямой АС, то они параллельны и между собой. И равны половине основанию АС. Таким образом, PSEF представляет собой параллелограмм.

Рис.6 Задача. Точки А, В, С, D не лежат в одной плоскости.

Пример 3

Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и ВС, АС и BD, AD и BC пересекаются в одной точке.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем отрезки EP, VS, FT, которые соединят середины сторон AB и CD, BC и AD, AC и BD соответственно (Рис.7).

Из предыдущей задачи нам известно, что четырехугольник EVPS, вершины которого являются серединами отрезков АВ, ВС, СD и AD, есть параллелограмм, у которого EP и VS диагонали. Эти диагонали пересекаются в точке О и делятся этой точкой пополам.

Теперь рассмотрим четырехугольник VTSF. Данный четырехугольник также является параллелограммом, так как его вершины — это середины отрезков BC, BD, AC и AD. А его диагонали VS и FT пересекаются в точке О и делятся этой точкой пополам.

Так как у отрезка VS середина одна, т.е. точка О, то все три диагонали EP, VS и FT пересекаются в этой точке.

Рис.7 Задача. Даны четыре точки А, В, С, D, не лежащие в одной плоскости.

Пример 4

Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость α по параллельным прямым, то прямая а параллельна плоскости α.

Доказательство:

Пусть даны две плоскости β и γ, пересекающиеся по прямой а (Рис.8). Эти плоскости пересекают плоскость α по параллельным прямым b и с. Необходимо доказать, что прямая а параллельна плоскости α.

Прямая b — это множество точек, которые одновременно принадлежат плоскостям α и γ. Прямая с — это множество точек, которые одновременно принадлежат плоскостям α и β. Так как прямые b и с параллельны, то на этих прямых нет ни одной точки, которая одновременно принадлежала бы трем плоскостям.

Прямая а — это множество точек, которые принадлежат двум плоскостям β и γ. Допустим, что она пересекает плоскость α. Тогда на ней должна быть точка, которая принадлежала бы одновременно трем плоскостям. А следовательно, она одновременно лежала бы на прямых b и с. Но это противоречит условию задачи, так как прямые b и с не пересекаются. Следовательно, прямая а параллельна прямым b и с. А отсюда следует, что она параллельна плоскости α.

Рис.8 Задача. Докажите, что если две плоскости, пересекающиеся по прямой а.

Пример 5

Докажите, что если четыре прямые, проходящие через точку О, пересекают плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через точку О, тоже в вершинах параллелограмма.

Доказательство:

Пусть даны четыре прямые, проходящие через точку О, ОА, ОВ, ОС и OD (Рис.9). Они пересекают плоскость α в точках А, В, С и D соответственно. Проведем плоскость α’, параллельную плоскости α. Тогда прямые ОА, ОВ, ОС и OD пересекут плоскость α’ в точках A’B’C’D’.

Проведем плоскость β через точки А, В, A’, B’. Тогда прямые АВ и A’B’ не пересекаются, так как это прямые пересечения двух параллельных плоскостей α и α’ с секущей плоскостью β.

Отсюда следует, что прямые ВС и В’С’, CD и C’D’, AD и A’D’ параллельны. А так как АВ параллельна CD, а ВС параллельна AD, то следовательно, А’В’ параллельна C’D’, а В’С’ параллельна A’D’.

Таким образом, A’B’C’D’ также является параллелограммом.

Рис.9 Задача. Докажите, что если четыре прямые, проходящие через точку А.

🔍 Видео

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Главная > Учебные материалы > Математика: Стереометрия. Страница 2 1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей. 5.Примеры.

1 2 3 4 5 6 7 8

Рис. 1 Параллельность прямых в пространстве. Видео:Точка, прямая и отрезок. 2 часть. 7 класс.Скачать 2.Признак параллельности прямых Теорема. Две прямые, параллельные третьей прямой, параллельны. Доказательство. Пусть прямые а и b лежат в разных плоскостях и параллельны прямой с. Доказать, что прямые а и b параллельны между собой. (Рис.2) Проведем через прямую a и c плоскость α. Через прямые b и c плоскость β. Прямая с — прямая пересечения плоскостей α и β. Отметим на прямой а точку А. Проведем через точку А и прямую b плоскость γ. Тогда плоскость γ будет пересекать плоскость α по прямой а’. Прямая a’ либо паралельна прямой c, либо ее пересекает. Допустим прямая а’ пересекает прямую с. Тогда эта точка пересечения принадлежит плоскости β, т.к. прямая с принадлежит двум плоскостям α и β. А т.к. прямая а’ полностью принадлежит плоскости γ, а прямая b есть прямая пересечения плоскостей γ и β, то это означает, что она пересекает и прямую b. А это означает, что прямые b и c пересекаются, т.к. прямая a’ пересекает плоскость β только в одной точке, которая должна принадлежать двум прямым b и с. А это противоречит условию. Следовательно прямая a’ не пересекает прямую с. Она ей параллельна. Согласно аксиоме, на плоскости α, через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. И эта прямая а. Т.е. прямые а и а’ совпадают. Это значит, что прямые а и b параллельны. Рис.2 Признак параллельности прямых Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать 3. Признак параллельности плоскостей Теорема: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Доказательство. Пусть α и β данные плоскости. Прямая а параллельна прямой а 1 . Прямая b параллельна b 1 (Рис.3). Допустим, что плоскости α и β пересекаются по прямой с. Тогда прямая с должна пересекать, как минимум, одну из прямых на каждой плоскости. Пусть это будут прямые а и а 1 . Т.к. прямые а и а 1 параллельны, следовательно они пересекают прямую с в разных точках Е и Е 1 . Проведем через две параллельные прямые а и а 1 плоскость γ. Тогда точки Е и Е 1 , которые лежат на прямой с, будут принадлежать плоскости γ. Следовательно, прямая с полностью принадлежит плоскости γ. Отсюда следует, что: а ∈ α, γ. а 1 ∈ β, γ. с ∈ α, β,γ т.е. плоскости α и γ пересекаются по двум прямым а и с, а плоскости β и γ пересекаются по прямым а 1 и с. Рис. 3 Признак параллельности плоскостей. Согласно аксиоме стереометрии, это невозможно, т.к. две плоскости могут пересекаться только по одной прямой. И следовательно, наше предположение неверно. Плоскости α и β не пересекаются, они параллельны. Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать 4. Свойства параллельных плоскостей Теорема: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Доказательство. Пусть даны две параллельные плоскости α и β (Рис.4). Плоскость γ пересекает их по прямым а и b. Допустим, что прямые пересечения плоскостей пересекаются. Это прямые а и b’. Прямая а — это множество точек, принадлежащих плоскостям α и γ. А так как прямая b’ представляет собой множество точек, пренадлежащих двум плоскостям β и γ, то отсюда следует, что существует точка пересечения прямых а и b’, которая принадлежит плоскости α. И следовательно, плоскости α и β имеют общую точку. А это противоречит условию, т.к. плоскости α и β не пересекаются, они параллельны. Следовательно, прямые а и b лежат в одной плоскости и не пересекаются. Т.е. они тоже параллельны. Рис. 4 Свойства параллельных плоскостей.