Даны два единичных вектора угол между которыми 120

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Задача 22492 1. Даны векторы vector и vector и.

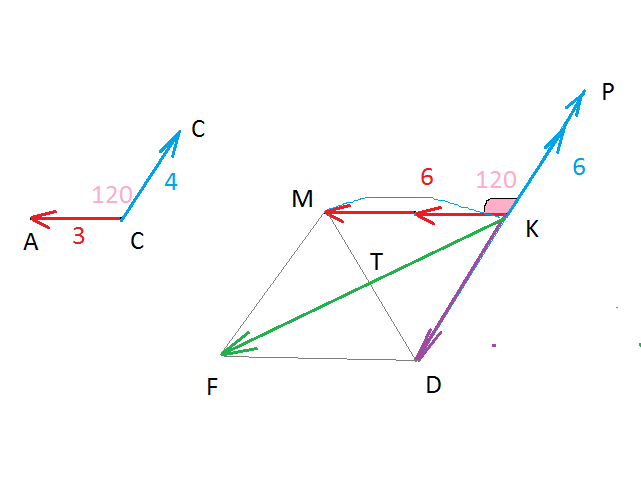
Условие

1. Даны векторы vector и vector и угол между ними равный 120°. Построить вектор vector = 2vector-1,5vector и определить его длину, если |vector| = 3, |vector| = 4.

Решение

Откладываем векторы от одной общей точки С
vector=vector
vector=vector

∠MKD=60 градусов, как смежный углу в 120 градусов.

Δ МKD — равнобедренный с углом 60 градусов при вершине, значит и другие его углы по 60 градусов и он равносторонний.

KT- высота равностороннего треугольника со стороной 6
КТ=6*sin60 градусов=6sqrt(3)/2=3sqrt(3)

|vector|=6sqrt(3)
О т в е т. 6sqrt(3)

Видео:Угол между векторами. 9 класс.Скачать

Дипломная работа

Пример. Зная векторы a и b, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a.

Решение. Обозначим AB=a, AC=b, CD=h, где CD ^ a, D-основание пер-

пендикуляра, опущенного из точки C на сторону a. По правилу сложения векторов имеем:
b + h = AD, h = AD — b. Поскольку AD çç a, то AD = l a.

Найдем значение l , используя ортогональность векторов
a и h: ah=0 или a( l a-b)=0, откуда l = ab /a2. Следовательно,
h = (ab /a2) a — b.

Пример. Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120о. Несобственный интеграл Математика Примеры вычисления интегралов Дифференциальные уравнения

Решение. Имеем: cos j = ab/ab, ab = (2m+4n) (m-n) = 2 m2 — 4n2 +2mn =
= 2 — 4+2cos120o = — 2 + 2(-0.5) = -3; a = ; a2 = (2m+4n) (2m+4n) =
= 4 m2 +16mn+16 n2 = 4+16(-0.5)+16=12, значит a = . b = ; b2 =
= (m-n)(m-n) = m2 -2mn+ n2 = 1-2(-0.5)+1 = 3, значит b = . Окончательно имеем: cos j = = -1/2, Þ j = 120o.

Зная векторы AB(-3,-2,6) и BC(-2,4,4),вычислите длину высоты AD треугольника ABC.

При каком значении векторы где , перпендикулярны?

Для нахождения длины вектора воспользуемся формулой: , для этого найдем проекции векторов на оси координат, так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат Направление вектора определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам Векторное произведение векторов

Матричный метод Если матрица А системы линейных уравнений невырожденная, т.е.
det A ¹ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A — 1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A — 1B называют матричным способом решения системы, или решением по методу обратной матрицы.

Видео:найти угол между единичными векторамиСкачать

Угол между векторами.

Видео:9 класс, 17 урок, Угол между векторамиСкачать

Формула вычисления угла между векторами

Видео:Как находить угол между векторамиСкачать

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

📽️ Видео

Скалярное произведение векторов. 9 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

105. Угол между векторамиСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Разложение вектора по базису. 9 класс.Скачать

Единичный векторСкачать

9 класс, 18 урок, Скалярное произведение векторовСкачать

Коллинеарность векторовСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать