Дано abcda1b1c1d1 параллелепипед изобразите векторы равные

Видео:№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

Ваш ответ

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

решение вопроса

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,949
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать

1. abcda1b1c1d1 — параллелепипед, изобразите на рисунке векторы равные 1)ab + b1c1 + dd1 + cd 2)bd1 — b1c1 2?

Математика | 10 — 11 классы

1. abcda1b1c1d1 — параллелепипед, изобразите на рисунке векторы равные 1)ab + b1c1 + dd1 + cd 2)bd1 — b1c1 2.

Точка S — середина ребра АС тетраэдра DABC, точка N — середина отрезка DS.

Выразите вектор BN через векторы BA = а , ВС = с , BD = d.

3. В треугольнике KLM точка С — пересечение медиан, Т — середина отрезка NC(N не лежит в плоскости KLM) Разложите вект.

МТ по векторам СВ, CD, СС1.

1. В параллелепипеде верны следующие равенства :

Видео:№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

Даны векторы а(2 ; 0), в(1 ; 2) , с( — 3 ; ) А) найдите значение м при котором ; векторы в и а — 2с перпендикулярны В)Будут ли эти коллинеарные векторы со направлены 3, В параллелограмме АВСД точка М ?

Даны векторы а(2 ; 0), в(1 ; 2) , с( — 3 ; ) А) найдите значение м при котором ; векторы в и а — 2с перпендикулярны В)Будут ли эти коллинеарные векторы со направлены 3, В параллелограмме АВСД точка М — середина стороны СД, точка К_ середина стороны ВС.

Выразите через векторы АВ = а и АД = в : векторы МВ и КМ.

Видео:№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

Дан тетраэдр DABC, K — середина ребра AC, M — середина отрезка KD, вектор DA = вектору a, вектор DB = вектору b, вектор DC = вектору c?

Дан тетраэдр DABC, K — середина ребра AC, M — середина отрезка KD, вектор DA = вектору a, вектор DB = вектору b, вектор DC = вектору c.

Разложите вектор BM по векторам a, b, c.

Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

ПОМОГИТЕ ПОЖАЛУЙСТА?

Точки D и E — середины сторон AB и BC треугольника ABC, а точки M и N лежат на стороне AC, причем AM = MN = NC, вектор CN = вектору a, вектор CE = вектору b

а) выразите векторы CD, MB, MD через векторы a и b.

Б) Докажите с помощью векторов , что MB ll NE.

Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Даны Точки А(2) и В(2½)?

Даны Точки А(2) и В(2½).

Найдите координату точки С — середины отрезка АВ, координату точки D — середины отрезка СВ, координату точки Е — середины отрезка СD.

Изобразить эти точки на координатной оси.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

DABC — тетраэдр?

Середина BC — точка E, а середина АЕ — точка О.

Найти вектор DO через векторы DA = a, DB = b, DC = c.

Заранее ОГРОМНОЕ СПАСИБО).

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Помогите пожалуйста по математике даны точки А(2) и В (2 1 / 2) найдите коортиинаты точки С — середины отрезка АВ точка D — середины отрезка СВ точки У середины отрезка CD изобразите эти точки на коор?

Помогите пожалуйста по математике даны точки А(2) и В (2 1 / 2) найдите коортиинаты точки С — середины отрезка АВ точка D — середины отрезка СВ точки У середины отрезка CD изобразите эти точки на координатном луче.

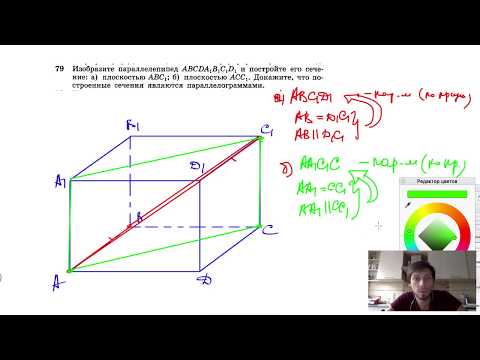
Видео:№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

Даны точки А(2) и В(2 1 / 2)?

Даны точки А(2) и В(2 1 / 2).

Найдите координаты Точки С середины отрезка АВ точки Д середины отрезка СВ точки Е середины отрезка АВ.

Видео:10 класс, 43 урок, Компланарные векторыСкачать

Даны Точки А(2) и В(2½)?

Даны Точки А(2) и В(2½).

Найдите координату точки С — середины отрезка АВ, координату точки D — середины отрезка СВ, координату точки Е — середины отрезка.

Видео:№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

Срочно, даю 39 баллов?

Срочно, даю 39 баллов!

1. Даны точки А (2) и В (2 1 / 2).

Найдите координаты : точки С — середины отрезка АВ, точки D — середины отрезка СВ, точки Е — Середины отрезка CD.

Изобразите эти точки на координатном луче.

Видео:№86. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

Дан параллелограмм ABCD?

Дан параллелограмм ABCD.

O точка пересечения диагоналей.

N середина стороны AB.

Найти сумму векторов AN и OD.

Разность векторов NC и OB.

На этой странице находится вопрос 1. abcda1b1c1d1 — параллелепипед, изобразите на рисунке векторы равные 1)ab + b1c1 + dd1 + cd 2)bd1 — b1c1 2?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

462 км растояние между портом Пирей и островом Родос.

Видео:№87. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью MNK, где точки М,Скачать

Презентация по геометрии в 10 классе на тему «Компланарные векторы. Правило параллелепипеда»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Компланарные векторы. Правило параллелепипеда

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости. Любые два вектора компланарны. *

Три вектора, среди которых имеются два коллинеарных, также компланарны. *

Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед. А О Е D C В B1 *

Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед. А О Е D C В B1 *

B C A1 B1 C1 D1 A D *

A B C A1 B1 C1 D1 D Любые два вектора компланарны. *

№355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1 Три вектора, среди которых имеются два коллинеарных, компланарны. *

№355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1 *

№355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1 Три вектора, среди которых имеются два коллинеарных, компланарны. *

№355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1

Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. Признак компланарности *

Докажем, что векторы компланарны. В1 *

Сложение векторов. Правило треугольника. b П О В Т О Р И М *

Сложение векторов. Правило параллелограмма. А В D C П О В Т О Р И М *

Сложение векторов. Правило многоугольника. П О В Т О Р И М *

Правило параллелепипеда. b

Теорема о разложении вектора по трем некомпланарным векорам. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. *

Докажем теперь, что коэффициенты разложения определяются единственным образом. Допустим, что это не так и существует другое разложение вектора – Это равенство выполняется только тогда, когда o o o *

В A С B1 C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: АВ + АD + АА1 A1 *

В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: DА + DC + DD1 A1 B1 *

В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: A1 B1 A1B1 + C1B1 + BB1 *

В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: A1 B1 *

В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: A1 B1 *

В A С C1 D1 №359 Дан параллелепипед АВСA1B1C1D1. Разложите вектор BD1 по векторам BA, ВС и ВВ1. A1 B1 *

В A С C1 D1 №359 Дан параллелепипед АВСA1B1C1D1. Разложите вектор B1D1 по векторам А1A, А1В и А1D1. A1 B1 = = =

Правило параллелепипеда a Пусть даны некоторые некомпланарные векторы c a , b, c b

Правило параллелепипеда С Отложим от некоторой точки О пространства векторы ОА=a , ОВ=b, ОС=c и построим паралле- c лепипед так, чтобы В отрезки ОА,ОВ,ОС были его рёбрами. О А b a

Правило параллелепипеда D С Диагональ OD этого параллелепипеда изобра- жает сумму векторов a , b , и c c О А b a

Правило параллелепипеда D С OD=a + b +c . Действительно, OD=OE + ED=(OA +AE)+ + ED= OA+ 0B + OC = = a +b +c В Е О А

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: а) АВ+ВD+DC

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: а) АВ+ВD+DC A D B C

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: а) АВ+ВD+DC A Решение. AB+BD= AD, AD+DC=AC D Ответ: АС B C

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: б) АD+CВ+DC

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: б) АD+CВ+DC A D B C

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: б) АD+CВ+DC A Решение. AD+DC= AC, AC+CB=AB D Ответ: АB B C

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: в) АB+CD+BC+DA

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: в) АB+CD+BC+DA A D B C

Решение задач № 379 Дан тетраэдр АВСD. Найдите сумму векторов: в) АB+CD+BC+DA A Решение. AB+BC= AC, AC+CD=AD, AD+DA=0 D Ответ: 0 B C

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А1

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А1 B1 С1 А1 D1 B С А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А1 B1 С1 А1 D1 Решение AB+AD = АС АС + A А1 = АС1 B С Ответ : АС1 А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D1

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D1 B1 С1 А1 D1 B С А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D1 B1 С1 А1 D1 Решение DA+DC = DB DB + DD1 = DB1 B С Ответ : DB1 А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А1B1+С1B1 +ВВ1

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А1B1+С1B1 +ВВ1 B1 С1 А1 D1 B С А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А1B1+С1B1 +ВВ1 B1 С1 А1 D1 Решение А1B1+С1B1= D1 А1+ А1B1 = D1В1 D1В1 + ВВ1 = DВ + ВВ1 = DB1 B С Ответ : DB1 А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) A1 A+A1D1 +AВ

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) А1А+A1D1 +AВ B1 С1 А1 D1 B С А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) А1А+A1D1 +AВ B1 С1 А1 D1 Решение А1A+A1D1= A1D1+ D1D = A1D A1D + AВ = A1D + DC = A1C B С Ответ : A1C А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) B1A1+BB1 +ВC

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : д) B1А 1 +BB1 +BC B1 С1 А1 D1 B С А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : д) B1А 1 +BB1 +BC B1 С1 А1 D1 Решение B1A 1 +BB1= BA1 BA1 + ВC = BA1 + A1D 1 = BD1 B С Ответ : BD1 А D

Решение задач № 358. Дан параллелепипед ABCDА1B1С1D1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) B1A1+BB1 +ВC

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : а) АB +B1C1 +DD1+CD B1 С1 А1 D1 B С А D

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : а) АB +B1C1 +DD1+CD B1 С1 А1 D1 Решение AB +B1C1 = AB +BC = AC AC + CD + DD1 = AD1 B С Ответ : AD1 А D

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : б) B1C1 + АB + DD1+CB1+ BC + AA1 B1 С1 А1 D1 B С А D

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : б) B1C1 + АB + DD1+CB1+ BC + AA1 B1 С1 А1 D1 Решение AB +B1C1 = AB +BC = AC AC + CB1 = AB1 BC + AA1 = BA1 ; AB1 + BA1 = AC1 B С Ответ : AС1 А D

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : в) BА + АC + CB+DC + DA B1 С1 А1 D1 B С А D

Решение задач № 380. Дан параллелепипед ABCDА1B1С1D1.. Найдите сумму векторов : в) BА + АC + CB+DC + DA B1 С1 А1 D1 Решение DC+DA+BA +AC + CB = DB B С Ответ : DB А D

Решение задач № 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что ОА1+ОВ1+ОС1=ОА+ОВ+ОС

Решение задач № 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что ОА1 +ОВ1+ОС1=ОА+ОВ+ОС В С1 А1 А В1 С

Решение задач № 384 Точки А1, B1, С1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите , что ОА1 +ОВ1+ОС1=ОА+ОВ+ОС В Доказательство ОС+СА1 =ОА1 ; ОА1 +А1В=ОВ; СА1+А1В=1/2СВ, значит ОС — ОА1=ОА1-ОВ отсюда следует, что ОС+ОВ=2ОА1 Аналогично, ОС+ОА=2ОВ1 и ОВ+ОА=2ОС1 С1 А1 Складывая почленно три полученные равенства, получим равенство, которое необходимо доказать. А В1 С

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 937 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 497 468 материалов в базе

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Дистанционные курсы для педагогов

Другие материалы

• 13.04.2020
• 4005

• 13.04.2020
• 187

• 13.04.2020
• 166

• 13.04.2020
• 128

• 13.04.2020
• 760

• 13.04.2020
• 380

• 13.04.2020
• 1875

• 13.04.2020
• 131

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 13.04.2020 1872 —> —> —> —>
• PPTX 2.9 мбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Филиппова Татьяна Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 131522
• Всего материалов: 293

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Каждый второй российский студент недоволен своим вузом

Время чтения: 1 минута

Минспорта утвердило программу подготовки киберспортсменов

Время чтения: 1 минута

В Сыктывкаре школьников переведут на дистанционное обучение

Время чтения: 1 минута

Школы Северной Осетии переведут на дистанционное обучение

Время чтения: 1 минута

УрФУ возглавил рейтинг медиаактивности вузов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📺 Видео

№85. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где КСкачать

№80. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечения плоскостями АВС1Скачать