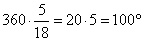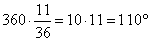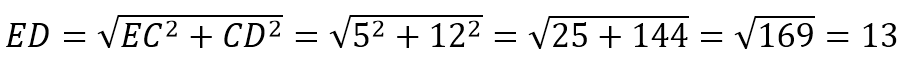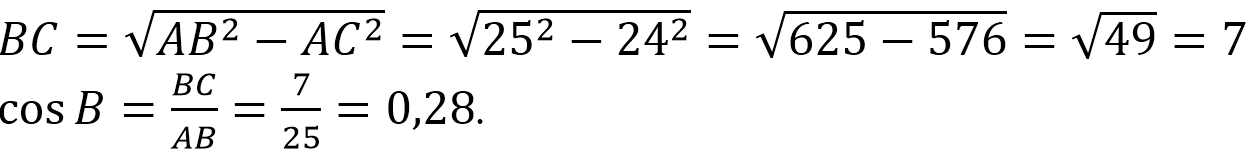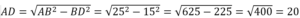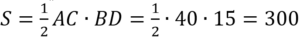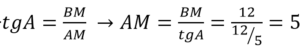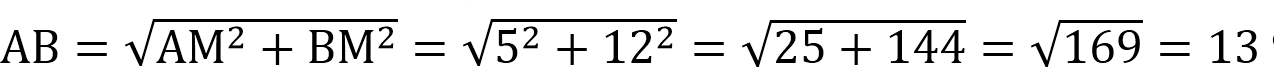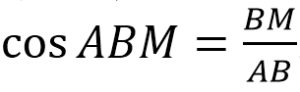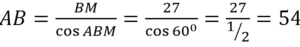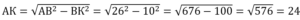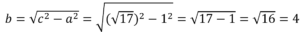Дан равнобедренный треугольник авс ав вс в окружности

Геометрия | 5 — 9 классы

В равнобедренный треугольник АВС (АВ = ВС) вписали окружность.

Касательная L к окружности, параллельна прямой АС, пересекает стороны АВ и ВС в точках Т и Р соответственно.

Известно, что периметр четырёхугольника АТРС равен 30 см.

Вычислите длину радиуса окружности.

АТРС — равнобедренная трапеция.

У трапеции, описанной около четырехугольника (трапеции в нашем случае) сумма противоположных сторон равна.

ТР + АС = 30 / 2 = 15

АС = 12см, тогда ТР = 15 — 12 = 3см

АТ + РС = 15 и так как АТ = РС, то АТ = РС = 15 / 2 = 7, 5см

Диаметр окружности является ее высотой ТН (опусти перпендикуляр из Т на АС).

АН = (АС — ТР) / 2 = (15 — 12) / 2 = 4, 5см

По теоремме пифагора :

ТН = √(АТ ^ 2 — AH ^ 2) = √(56, 25 — 20, 25) = √36 = 6см

ТН — это диаметр, а радиус равен его половине, т.

Е. r = ТР / 2 = 6 / 2 = 3см.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Периметр треугольника АВС равен 9 радиус вписанной в этот треугольник окружности равен √3?

Периметр треугольника АВС равен 9 радиус вписанной в этот треугольник окружности равен √3.

Найти расстояние от центра вписанной окружности до вершины В, если длина стороны АС равна 3, 5.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

1. Длина ребра куба ABCDA1B1C1D1 равна 4см?

1. Длина ребра куба ABCDA1B1C1D1 равна 4см.

Вычислите длину радиуса окружности, вписанной в треугольник DA1C1.

2. в равнобедренный треугольник ABC(AB = BC) вписана окружность.

Касательная l к окружности, параллельная прямой AC, пересекает стороны AB и BC в точках T и P соответственно.

Известно, что периметр четырехугольника ATPC равен 30 см и AC = 12см.

Вычислите длину радиуса окружности.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Помогите пожалуйста?

Окружность касается всех сторон треугольника АВС.

Известно, что точки касания являются серединами сторон треугольника.

Вычислите длину радиуса окружности, если известно, что периметр треугольника АВС равен 18 см.

Видео:ОГЭ 2022 Демоверсия. 25 задание | Основание AC равнобедренного треугольника ABC равно 12.....Скачать

ПОМОГИТЕ ПОЖАЛУЙСТА?

Точки Р и О лежат соответственно на сторонах АВ и АС равностороннего треугольника АВС.

Известно, что в прапецию врос можно вписать окружность и ее периметр равен 32 см вычислить площадь треугольника АВС.

Видео:Равнобедренный треугольник. 7 класс.Скачать

Радиус окружности, описанной около правильного четырёхугольника равен 6√2?

Радиус окружности, описанной около правильного четырёхугольника равен 6√2.

Вычислите отношение периметра этого четырёхугольника к длине радиуса вписанной в него окружности.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

В Пямоугольном треугольнике АВС угол А прямой, Катет АВ равен а, радиус вписанной окружности равен r?

В Пямоугольном треугольнике АВС угол А прямой, Катет АВ равен а, радиус вписанной окружности равен r.

Вписанная окружность касается АС в точке D.

Найти хорду, соединяющую точки пересечения окружности с прямой BD.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

В равнобедренный треугольник ABC (AB = AC) вписана окружность , касательная L к окружности параллельна прямой BC пересекает стороны AB и AC в точках K и O?

В равнобедренный треугольник ABC (AB = AC) вписана окружность , касательная L к окружности параллельна прямой BC пересекает стороны AB и AC в точках K и O.

Известно что периметр четырехугольника BTOC = 45 cм и TO : BC как 1 : 4 , вычислите радиус окружности.

Видео:Задание 6 ЕГЭ по математике. Урок 13Скачать

В прямоугольном треугольнике АВС угол С = 90, вписанная окружность касается стороны ВС в точке К?

В прямоугольном треугольнике АВС угол С = 90, вписанная окружность касается стороны ВС в точке К.

Известно, что АС = 24, а радиус вписанной окружности равен 7.

Найдите длину хорды, которую высекает прямая АК на вписанной окружности.

Видео:ЕГЭ 2023, сборник Ященко, вариант 36, задача 16 ЧАСТЬ 1Скачать

В угол А вписаны две окружности?

В угол А вписаны две окружности.

Общая касательная окружностей стороны угла в точках В и С какое из утверждений является верным а)окружность, радиус которой меньше, является вписанной в треугольник АВС.

Б) окружность, радиус которой больше, яляется вписанной в треугольник АВС.

Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

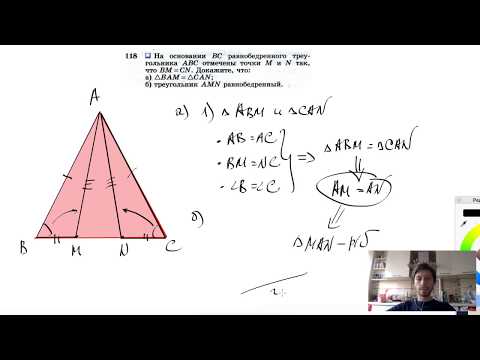
В равнобедренный треугольник АВС (АВ = ВС) вписана окружность?

В равнобедренный треугольник АВС (АВ = ВС) вписана окружность.

Касательная l к окружности, параллельная прямой АС, пересекает стороны АВ и ВС в точках Е и Р соответственно.

Известно, что периметр четырехугольника АТРС равен 30 см и АС = 12 см.

Вычислите длину радиуса окружности (рисунок).

На этой странице сайта размещен вопрос В равнобедренный треугольник АВС (АВ = ВС) вписали окружность? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

∠АДС = 44(по св — ву вписанного четырехугольника) изΔАСД ; ∠АСД = 54, ∠АВД = ∠АСД = 54(т. К опираются на одну дугу) ∠ДВС = ∠ДАС = 82⇒∠АВС = 82 + 54 = 138.

Решение задания смотри на фотографии.

Решения даны на фото.

1. а) Продолжаем прямую А1М до пересечения с продолжением ркбра В1В в точку Р. Точка Р принадлежит и прямой А1Р(А1М) и плоскости ВВ1С1, поскольку прямая В1Р принадлежит этой плоскости. Значит точка Р т является искомой точкой. Б)Точки Р и С1 прина..

8 + 3 + 1 = 12 V = a * b * c x ^ 3 = 8x * 3x * 1x 24 = 24x x = 1 a = 8x = 8 b = 3x = 3 c = 1x = 1 Sp = 2(ab + bc + ac) = 2(8 * 3 + 3 * 1 + 8 * 1) = 2(24 + 3 + 8) = 2 * 35 = 70 Ответ : площадь поверхности равна 70.

В периодах отначала к периода к концу (слева направо) усиливаются кислотные (неметаллические) свойства и ослабевают основные (металлические) свойства в связи с увеличением количества электронов на внешнем электронном уровне. В группах от начала к ко..

Длина и ширина и закрашенного прямоугольника равны C) 0, 25 см ; 1 см.

Дам совет в это значит умножить например больше в 5 раз тоесть надо умножить значит 4 умножить на 20 равно 100 АС равно 100.

Так как угол B прямой, то треугольник PBK (вписанный в окружность) — прямоугольный, а отрезок PK — ее диаметр (по свойству вписанного в окружность прямоугольного треугольника). Стало быть BH (тоже диаметр окружности) = PK = 12.

1) Т. К. треугольник ABC равнобедренный, то угол CAM = углу CBA = 50 градусов ; 2) Т. К. AM — биссектриса, то угол CAM = 1 / 2 угла CAB угол CAM = 25 градусам.

Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

Задание №15 ЕГЭ по математике базового уровня

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Планиметрия

В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.

Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня

Вариант 15МБ1

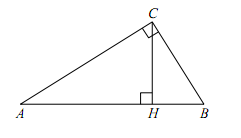
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.

Алгоритм выполнения:

1. Вспомнить определение косинуса угла.
2. Записать выражение для нахождения косинуса угла.
3. Выразить неизвестную величину.
4. Вычислить.

Решение:

Вспомним определение косинуса угла.

Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.

Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.

Прилежащий к углу А катет – АН.

Получим cos A = АН/АС.

Выразим неизвестную величину.

АН = АС · cos A = 4 · 0,8 = 3,2

Вариант 15МБ2

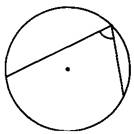
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 5/18 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ3

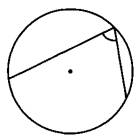
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 11/36 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ4

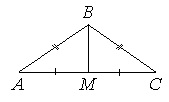
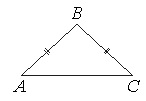
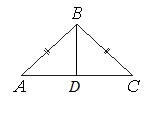
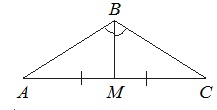
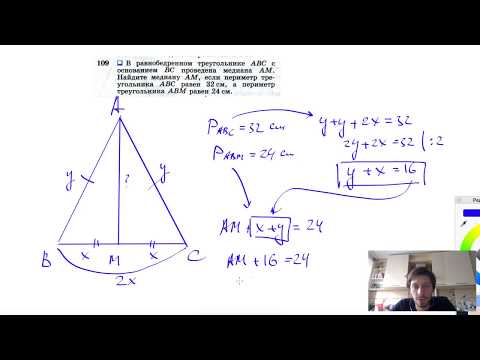
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.

Алгоритм выполнения

1. Определяем

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение:

Если АВ=ВС, то ∆АВС – равнобедренный.

В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=90 0 , и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.

По т.Пифагора АМ 2 +ВМ 2 =АВ 2 . Отсюда: .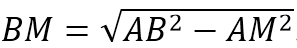

Т.к. АМ медиана, то

.

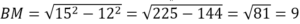
Вариант 15МБ5

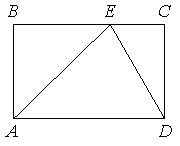
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

Алгоритм выполнения

1. Находим ЕС.
2. Определяем значение СD.
3. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.

Решение:

Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.

Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.

Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=90 0 , и ∆ЕСD прямоугольный.

Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 . Получаем:

Вариант 15МБ6

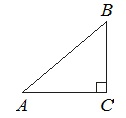
В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B.

Алгоритм выполнения

1. По т.Пифагора находим величину катета ВС.
2. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.

Решение:

Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .

Вариант 15МБ7

В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.

Алгоритм выполнения

1. Из вершины В

Проводимость — способность живой ткани проводить возбуждение.

Решение

В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.

Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →

Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.

Площадь ∆АВС равна:

Вариант 15МБ8

В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.

Алгоритм выполнения

1. Доказываем, что ∆АВМ прямоугольный.
2. Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
3. Из ∆АВМ по теореме Пифагора находим АВ.

Решение:

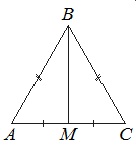
Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.

Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →

Вариант 15МБ9

В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.

Алгоритм выполнения

1. Определяем величину угла АВМ.
2. Доказываем, что ∆АМВ прямоугольный.
3. Находим АВ, используя формулу-определение для косинуса.

Решение:

По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет

Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.

В прямоугольного ∆АМВ:

Вариант 15МБ10

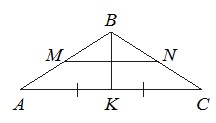
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.

Алгоритм выполнения

1. Доказываем, что ∆АКВ прямоугольный.
2. Из ∆АКВ по т.Пифагора находим АК.
3. Находим АС как 2АК.
4. Находим МN как среднюю линию.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 90 0 , и ∆АКВ прямоугольный.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 .

Поскольку ВК медиана, то АС=2АК=2·24=48.

Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).

Вариант 15МБ11

В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.

Алгоритм выполнения

1. Находим длину отрезков АМ и МС как половину от АС.
2. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.

Решение:

Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.

По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.

Вариант 15МБ12

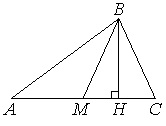
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.

Алгоритм выполнения

1. Находим величину 2-го (неизвестного) катета по т.Пифагора.
2. Определяем площадь треугольника как полупроизведение катетов.

Решение:

Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.

По т.Пифагора a 2 +b 2 =c 2 . Отсюда:

Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.

Вариант 15МБ13

В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.

Алгоритм выполнения

1. Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
2. Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
3. Из ∆АКВ по т.Пифагора находим АВ.

Решение:

Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.

Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Получаем:

Видео:Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Дан равнобедренный треугольник АВС, АВ = ВС = 8 см, ∠ АВС = 120°. Определите: а) радиус его описанной окружности;

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Ваш ответ

Видео:Построение медианы в треугольникеСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,006
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

📺 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

ОГЭ Задание 25 Доказательство параллельности прямыхСкачать

№120. В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. На сторонах АВ и СВСкачать

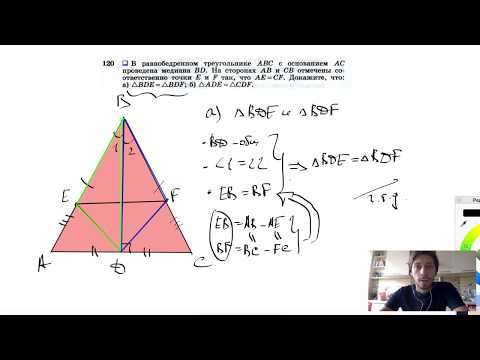
В треугольнике ABC AC = BC, высота AH равна 20, AB = 25. Найдите косинус BAC.Скачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать