- Онлайн калькулятор
- Как посчитать площадь равностороннего треугольника зная длину равных сторон
- Формула
- Пример
- Как посчитать площадь равностороннего треугольника зная его высоту
- Формула
- Пример
- Как посчитать площадь равностороннего треугольника зная радиус описанной окружности
- Формула
- Пример
- Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности
- Формула
- Пример
- Как посчитать площадь равностороннего треугольника зная его периметр
- Формула
- Пример
- Как найти площадь треугольника
- По формуле Герона
- Через основание и высоту
- Через две стороны и угол
- Через сторону и два прилежащих угла
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника через стороны
- Площадь равнобедренного треугольника через основание и угол
- Площадь равностороннего треугольника через стороны
- Площадь равностороннего треугольника через высоту
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь треугольника через радиус описанной окружности и три стороны
- Площадь треугольника через радиус вписанной окружности и три стороны
- Чему равна и как найти площадь равностороннего треугольника
- Признаки и свойства фигуры
- Расчет через сторону
- Расчет по высоте
- Расчет через окружности
- 🎦 Видео
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Онлайн калькулятор
Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину равных сторон (a)
- высоту (h)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
- периметр треугольника (P)
Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).
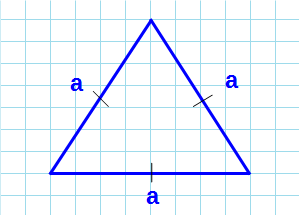
Как посчитать площадь равностороннего треугольника зная длину равных сторон
Чему равна площадь равностороннего треугольника если длина стороны ?
Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?
Формула
Пример
Если сторона a = 2 см, то:
S = √3 /4 ⋅ 2² = 1.732 /4 ⋅ 4 ≈ 1.732 см 2
Как посчитать площадь равностороннего треугольника зная его высоту
Чему равна площадь равностороннего треугольника если его ?
Какова площадь равностороннего треугольника (S) если известна его высота (h)?
Формула
Пример
Если высота h = 3 см, то:
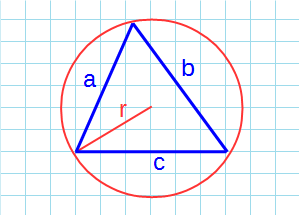
Как посчитать площадь равностороннего треугольника зная радиус описанной окружности
Чему равна площадь равностороннего треугольника если радиус описанной окружности ?
Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?
Формула
Пример
Если радиус описанной окружности R = 4 см, то:
S = 3 ⋅ √3 /4 ⋅ 4² = 3 ⋅ 1.732 /4 ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см 2
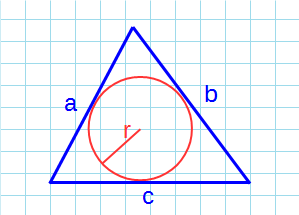
Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности
Чему равна площадь равностороннего треугольника если радиус вписанной окружности ?
Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?
Формула
Пример
Если радиус вписанной окружности r = 1 см, то:
S = 3⋅ √ 3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см 2
Как посчитать площадь равностороннего треугольника зная его периметр
Чему равна площадь равностороннего треугольника если его периметр ?
Какова площадь равностороннего треугольника (S) если известен его периметр (P)?
Формула
Пример
Если периметр P = 8 см, то:
S = √3 /36 ⋅ 8² = 1.732 /36 ⋅ 64 ≈ 3 см 2
Видео:Радиус описанной окружностиСкачать

Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
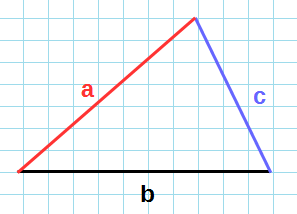
Формула Герона для нахождения площади треугольника:
Через основание и высоту
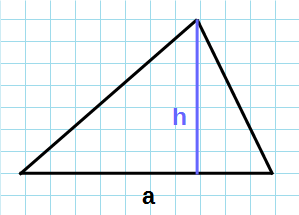
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
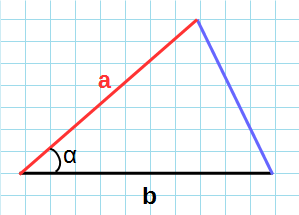
Формула нахождения площади треугольника через две стороны и угол между ними:
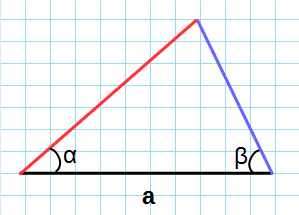
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
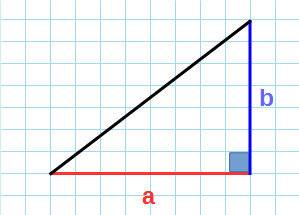
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
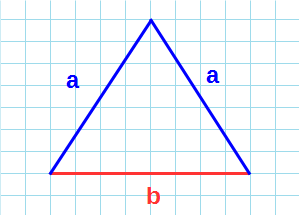
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
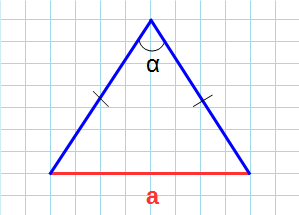
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
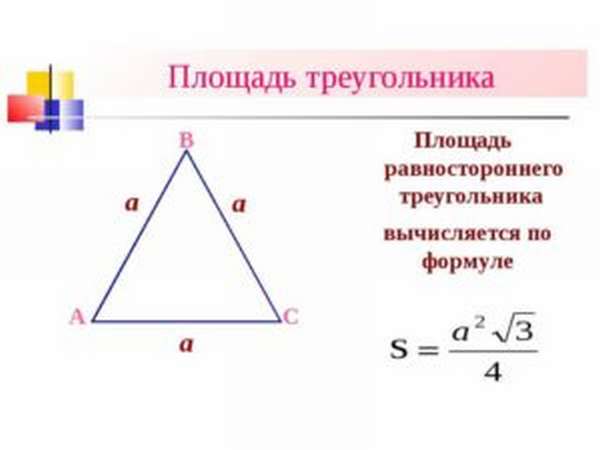
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
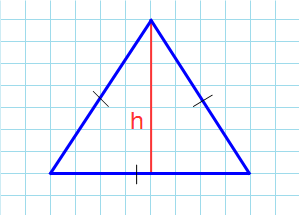
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
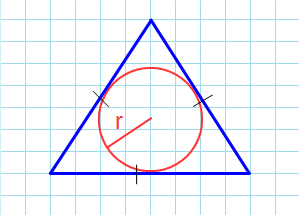
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
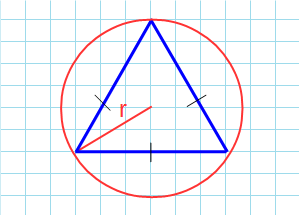
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Чему равна и как найти площадь равностороннего треугольника
Равносторонний треугольник — это самый простой правильный многоугольник из возможных. При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Признаки и свойства фигуры
Для того чтобы рассчитать его площадь необходимо понимать свойства и признаки, которыми он обладает. Можно выделить следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана выпущенные из одного угла будут совпадать.
- Любая сторона равностороннего треугольника равна двум другим.
- Центр правильного треугольника будет являться центром для вписанной и описанной окружности.
- Является частным случаем равнобедренного треугольника.
Важно! Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним. 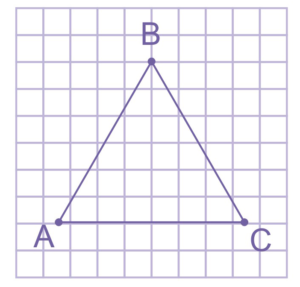
Дополнительно этот частный случай фигуры обладает следующими свойствами:
- Средняя линия, которая делит две боковые стороны пополам, равняется половине основания, параллельно которому она располагается.
- Сумма всех его углов не превышает 180 градусов.
- Радиус вписанной окружности рассчитывается по следующей формуле r =
, а описанной согласно выражению R =
.
- Радиус описанной окружности в правильном треугольнике в 2 раза больше радиуса вписанной.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Расчет через сторону
Существует множество способов расчета площади этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самая популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: 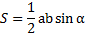
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все углы этой фигуры равны, и равняются 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется 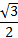
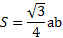
Учитывая то, что все стороны этой фигуры равны, то преобразованное выражение даст такой результат: 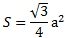
Данная формула отлично подойдет в случае, если известна величина стороны этой фигуры. В таком виде вычислять данный показатель гораздо легче и быстрее.
Те, кто помнит формула Герона, знают, как найти площадь этой фигуры. В процессе преобразования выражение изменится в представленное выше. Площадь этой фигуры по Герону рассчитывается так: 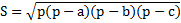
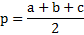
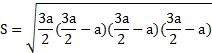
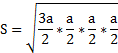
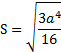
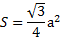
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Расчет по высоте
Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: 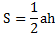
Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: 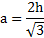
Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: 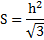
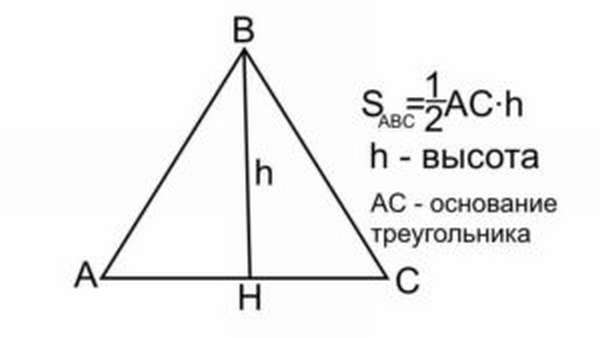
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Расчет через окружности
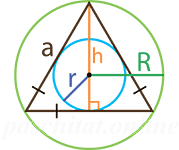
В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.
Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу 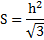
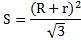
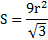
Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: 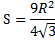
Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением 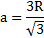
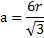
Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: 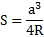
Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.
Площадь равностороннего треугольника
Площадь равностороннего треугольника, вписанного в окружность
Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
🎦 Видео
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы для радиуса окружности #shortsСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

№1117. Найдите площадь круга, вписанного: а) в равносторонний треугольник со стороной а;Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ПЛОЩАДЬ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА за 20 секунд!Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Формулы для равностороннего треугольника.Скачать

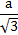 , а описанной согласно выражению R =
, а описанной согласно выражению R = 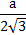 .
.