Дан пространственный четырехугольник m и n середины сторон

Дано: АВСD-пространственный четырехугольник.

Рассмотрим треугольник АВС:

М-середина АВ, N-середина ВС

Значит, MN-средняя линия треугольника АВС.

Рассмотрим треугольник АDC:

Треугольники ADC и DEK- подобные (по второму признаку подобия треугольников), т.к угол D-общий, а его стороны пропорциональны:

Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

А так как два эти треугольника подобны, то КЕ||AC

Так как KE||AC, MN||AC => KE||MN.

По определению трапеции, четырехугольник называется трапецией, если две его стороны параллельны, а две другие стороны не параллельны.

Докажем, что стороны КМ, EN не параллельны друг другу.

Значит, стороны KM, EN не могут быть параллельными в связи с разным отношением сторон.

Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2?

Алгебра | 10 — 11 классы

ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

1)Выполните рисунок к задаче.

Рисунок задачи во вложении ниже.

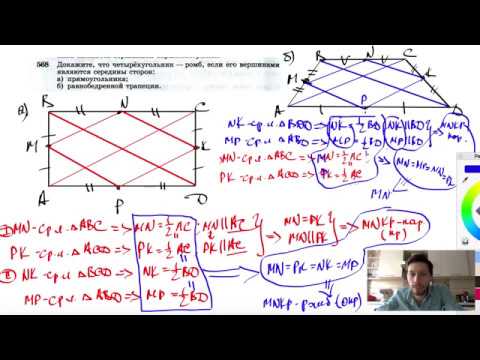
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно?

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно.

Найдите отношение площади четырехугольника abcd к площади четырёхугольника klmn.

Видео:Решение задач пространственный четырехугольникСкачать

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции?

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции.

Найдите периметр четырёхугольника NFGD если средняя линия трапеции равна 10 см, а её боковая сторона — 8 см.

Видео:№ 43 - Геометрия 10-11 класс АтанасянСкачать

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС?

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС.

Выразите через векторы А͞В = а͞ и А͞D = b͞ векторы М͞В и К͞М.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принад?

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принадлежит множеству A, но не принадлежит множеству B б) принадлежит множеству B, но не принадлежит множеству A в) принадлежит множеству A пересечённая с B?

Видео:Задание №43 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2?

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α?

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α.

Принадлежит ли плоскости середина отрезка АВ.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см?

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см.

Видео:Задание №47 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 прин?

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 принадлежит Q?

Видео:Как строить сечения параллелепипедаСкачать

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9?

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9.

Видео:Удары по Харькову и Херсону, В Беларуси пришли за родственниками. Бойко, Филипенко, ГринСкачать

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9)?

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9).

Вы перешли к вопросу ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2?. Он относится к категории Алгебра, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Алгебра. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Контрольная работа

Контрольная работа №1.

№1. Основание АD трапеции ABCD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках E и F соответственно.

а) Каково взаимное положение прямых EF и AB?

б) Чему равен угол между прямыми EF и AB, если ? Поясните ответ.

№2. Дан пространственный четырехугольник ABCD, в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.

а) Выполните рисунок к задаче.

б) Докажите, что полученный четырехугольник есть ромб.

№1. Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, а K – середина стороны DC.

а) Каково взаимное положение прямых PK и AB?

б) Чему равен угол между прямыми PK и AB, если и ? Поясните ответ.

№2. Дан пространственный четырехугольник ABCD, в котором M и N – середины сторон AB и BC соответственно.

.

а) Выполните рисунок к задаче.

б) Докажите, что четырехугольник MNEK есть трапеция.

Контрольная работа №2.

№1. Прямые а и b лежат в параллельных плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

№2. Через точку О, лежащую между параллельными плоскостями и , проведены прямые l и m. Прямая l пересекает плоскости и в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если , .

№3. Изобразите параллелепипед и постройте его сечение плоскостью, проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и DD1.

№1. Прямые а и b лежат в пересекающих плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

№2. Через точку О, не лежащую между параллельными плоскостями и , проведены прямые l и m. Прямая l пересекает плоскости и в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если , .

№3. Изобразите тетраэдр и постройте его сечение плоскостью, проходящей через точки М и N, являющиеся серединами ребер DC и ВС и точку K, такую, что .

Контрольная работа №3.

№1. Диагональ куба равна 6 см. Найдите:

б) косинус угла между диагоналями куба и плоскостью одной из его граней.

№2. Сторона AB ромба ABCD равна a, один из углов равен 60°. Через сторону AB проведена плоскость на расстоянии 0,5a, от точки D.

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла DABM, .

в) найдите синус угла между плоскостью ромба и плоскостью .

№1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна см, а его измерения относятся как 1:12 Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

№2. Сторона квадрата ABCD равна a. Через сторону AD проведена плоскость на расстоянии 0,5a, от точки B.

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла BADM, .

в) найдите синус угла между плоскостью квадрата и плоскостью .

Контрольная работа №4.

№1. Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна a. Ребро DA перпендикулярно к плоскости основания, а плоскость DBC составляет с плоскостью ABC угол в 30°. Найдите площадь боковой поверхности пирамиды.

№1. Основание прямого параллелепипеда является ромб ABCD, сторона которого равна a и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь полной поверхности параллелепипеда.

№1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, . Найдите площадь поверхности пирамиды.

№1. Основание прямого параллелепипеда является параллелограмм ABCD, сторона которого равна и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а) меньшую высоту параллелограмма;

б) угол между плоскостью и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь полной поверхности параллелепипеда.

К-1. Аксиомы стереометрии. Расположение прямых и плоскостей.

№1. Прямые a и b пересекаются. Прямая c является скрещивающейся с прямой a. Могут ли прямые b и c быть параллельными?

№2. Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки M и N.

а) Докажите, что .

б) Найдите BC, если , .

№3. Прямая MА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.

а) Докажите, что MА и BC – скрещивающиеся прямые.

б) Найдите угол между прямыми MА и BC, если .

№1. Прямые a и b пересекаются. Прямые a и c параллельны. Могут ли прямые b и c быть скрещивающимися?

№2. Плоскость проходит через основание AD трапеции ABCD. M и N – середины боковых сторон трапеции.

а) Докажите, что .

б) Найдите AD, если, .

№3. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков AB и BC.

а) Докажите, что CD и EF – скрещивающиеся прямые.

б) Найдите угол между прямыми CD и EF, если .

№1. Прямая a параллельна плоскости , а прямая b лежит в плоскости . Определите, могут ли прямые a и b:

а) быть параллельными;

в) быть скрещивающимися.

№2. Точка M не лежит в плоскости трапеции ABCD, .

а) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.

б) Найдите длины этих средних линий, если , а средняя линия трапеции равна 16 см.

№3. Через вершину А квадрата ABCD проведена прямая KA, не лежащая в плоскости квадрата.

а) Докажите, что KА и CD – скрещивающиеся прямые.

б) Найдите угол между KА и CD, если , .

№1. Прямая a параллельна плоскости , а прямая b пересекает плоскость . Определите, могут ли прямые a и b:

а) быть параллельными;

в) быть скрещивающимися.

№2. Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причем ,

а) Докажите, что

б) Найдите KP и MN, если , .

№3. Точка M не лежит в плоскости ромба ABCD.

а) Докажите, что MC и AD – скрещивающиеся прямые.

б) Найдите угол между MC и AD, если , .

№1. Плоскости и пересекаются по прямой l. Прямая a параллельна прямой l, и является скрещивающейся с прямой b. Определите, могут ли прямые a и b:

а) лежать в одной из данных плоскостей;

б) лежать в разных плоскостях и ;

в) пересекать плоскости и .

В случае утвердительного ответа укажите взаимное расположение прямых a и b.

№2. Плоскость пересекает стороны AB и BC треугольника ABC в точках M и N соответственно, причем ,

а) Докажите, что .

б) Найдите AC, если .

№3. Точки А, B, C, D не лежат в одной плоскости. Найдите угол между прямыми АC и BD, если , , а расстояние между серединами отрезков AD и BC равно 5 см.

№1. Плоскости и пересекаются по прямой l. Прямые l и a пересекаются, а прямые l и b параллельны. Определите, могут ли прямые a и b:

а) лежать в одной из данных плоскостей;

б) лежать в разных плоскостях и ;

в) пересекать плоскости и .

В случае утвердительного ответа укажите взаимное расположение прямых a и b.

№2. Плоскость проходит через сторону AC треугольника ABC. Прямая пересекает стороны AB и BC в точках M и N соответственно, причем ,

а) Докажите, что .

б) Найдите MN, если .

№3. Точки А, B, C, D не лежат в одной плоскости. Найдите угол между прямыми АB и CD, если , а расстояние между серединами отрезков AD и BC равно 3 см.

К-2. Перпендикулярность прямых и плоскостей.

№1. КА – перпендикуляр к плоскости треугольника АВС. Известно что КВ ^ ВС.

а) Докажите, что треугольник АВС – прямоугольный.

б) Докажите перпендикулярность плоскостей КАС и АВС.

в) Найдите КА, если , , .

№2. Основание АС равнобедренного треугольника лежит в плоскости . Найдите расстояние от точки В до плоскости , если , , а двугранный угол между плоскостями АВС и равен 30°.

№3. Из точки А к плоскости проведены наклонные АВ и АС, образующие с плоскостью равные углы. Известно, что . Найдите углы треугольника АВС.

№1. КА – перпендикуляр к плоскости параллелограмма ABCD. Известно, что KD ^ CD.

а) Докажите, что ABCD – прямоугольник.

б) Докажите перпендикулярность плоскостей KAD и ABC.

в) Найдите АС, если , , .

№2. Катет АВ прямоугольного треугольника АВС () лежит в плоскости . Найдите расстояние от точки С до плоскости , если , , а двугранный угол между плоскостями АВС и равен 45°.

№3. Из точки А к плоскости проведены перпендикуляр АО и две равные наклонные АВ и АС. Известно, что . Найдите углы треугольника ВОС.

№1. КА – перпендикуляр к плоскости треугольника АВС. М – середина стороны ВС. Известно, что КМ ^ ВС.

а) Докажите, что треугольник АВС – равнобедренный.

б) Докажите перпендикулярность плоскостей КВС и КАМ.

в) Найдите площадь треугольника АВС, если , , см.

№2. Точка S удалена от каждой из вершин правильного треугольника АВС на см. Найдите двугранный угол SABC, если .

№3. Прямая АВ – ребро двугранного угла, равного 90°. Прямые АА1 и ВВ1 принадлежат разным граням данного угла и перпендикулярны к прямой АВ. Докажите, что АА1^ВВ1.

№1. КА – перпендикуляр к плоскости параллелограмма ABCD. О – точка пересечения АС и BD. Известно, что КО ^ BD.

а) Докажите, что ABCD – ромб.

б) Докажите перпендикулярность плоскостей KBD и КОА.

в) Найдите площадь ABCD, если , , .

№2. Точка S удалена от каждой из сторон правильного треугольника АВС на см. Найдите угол между прямой SA и плоскостью АВС, если .

№3. Прямые АА1 и ВВ1 – перпендикуляры к ребру АВ двугранного угла, принадлежащие разным граням угла. Докажите, что если АА1^ВВ1, то данный двугранный угол – прямой.

№1. Точка О лежит на биссектрисе угла АВС, равного 60°. DО – перпендикуляр к плоскости АВС.

а) Докажите, что точка D равноудалена от сторон угла АВС.

б) Пусть DA и DC – расстояния от точки D до сторон угла. Докажите перпендикулярность плоскостей DAC и DOB.

в) Найдите DB, если , .

№2. Равнобедренные треугольники АВС и АDC имеют общее основание АС, а двугранный угол ВАСD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если , а .

№3. В кубе АВСDA1B1C1D1 постройте и найдите линейный угол двугранного угла между плоскостями сечений АВ1С1D и СВ1А1D.

№1. DO – перпендикуляр к плоскости угла АВС, равного120°, причем точка О лежит внутри угла, а D равноудалена от его сторон.

а) Докажите, что ВО – биссектриса угла АВС.

б) Пусть DA и DC – расстояния от точки D до сторон угла. Докажите перпендикулярность плоскостей DOB и DAC.

в) найдите DO, если , .

№2. Равнобедренные треугольники АВС и ADC имеют общее основание АС, а двугранный угол BACD – прямой. Найдите тангенс двугранного угла между плоскостями BAD и АDС, если , а .

№3. В кубе АВСDA1B1C1D1 постройте и найдите линейный угол двугранного угла между плоскостями сечений CD1A1B и DA1B1C.

№1. Основание прямой призмы – прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.

№2. Боковое ребро правильной четырехугольной пирамиды равно

4 см и образует с плоскостью основания пирамиды угол 45°.

а) Найдите высоту пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро правильного тетраэдра DABC равно a. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.

№1. Основание прямой призмы – прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань – квадрат.

№2. Высота правильной четырехугольной пирамиды равна см, боковое ребро наклонено к плоскости основания под углом 60°.

а) Найдите боковое ребро пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро правильного тетраэдра DABC равно a. Постройте сечение тетраэдра, проходящее через середины ребер DA и AB параллельно ребру BC, и найдите площадь этого сечения.

№1. Основание прямого параллелепипеда – ромб с диагоналями 10 и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45°. Найдите площадь полной поверхности параллелепипеда.

№2. Основание пирамиды – правильный треугольник с площадью см2. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 30°.

а) Найдите длины боковых ребер пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через прямую B1C и середину ребра AD, и найдите площадь этого сечения.

№1. Основание прямого параллелепипеда – ромб с меньшей диагональю 12 см. Большая диагональ параллелепипеда равна см и образует с боковым ребром угол 45°. Найдите площадь полной поверхности параллелепипеда.

№2. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45°.

а) Найдите длины боковых ребер пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через точку C и середину ребра AD параллельно прямой DA1, и найдите площадь этого сечения.

№1. Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20 см. Найдите площадь полной поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро, – квадрат.

№2. Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны . Найдите площадь полной поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через середины ребер AA1, B1C1 и CD, и найдите площадь этого сечения.

№1. Основание прямой призмы – равнобедренный треугольник с основанием 24 м и боковой стороной 13 см. Найдите площадь полной поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро, – квадрат.

№2. Основание пирамиды – ромб с тупым углом . Все двугранные углы при основании пирамиды равны . Найдите площадь полной поверхности пирамиды, если ее высота равна H.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через середины ребер A1B1, CC1 и AD, и найдите площадь этого сечения.

К-4. Векторы в пространстве.

№1. Дан куб АВСDA1B1C1D1.

а) Назовите вектор с началом в точке D1, равный вектору .

б) Назовите вектор, равный .

б) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. MA – перпендикуляр к плоскости ромба ABCD. Разложите вектор по векторам .

№4. Векторы неколлинеарные. Найдите значение k, при которых векторы и коллинеарные.

№1. Дан куб АВСDA1B1C1D1.

а) Назовите вектор с концом в точке C1, равный вектору .

б) Назовите вектор, равный .

б) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. MB – перпендикуляр к плоскости треугольника ABC. Разложите вектор по векторам .

№4. Векторы неколлинеарные. Найдите значение k, при которых векторы и коллинеарные.

№1. Дан параллелепипед АВСDA1B1C1D1.

а) Назовите вектор с началом в точке D, равный вектору .

б) Назовите вектор, равный ; в) .

г) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка О не лежит в плоскости параллелограмма ABCD. Разложите вектор по векторам .

№4. Даны параллелограммы ABCD и ABC1D1. Докажите, что векторы компланарны.

№1. Дан параллелепипед АВСDA1B1C1D1.

а) Назовите вектор с концом в точке B1, равный вектору .

б) Назовите вектор, равный ; в) .

г) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка О не лежит в плоскости параллелограмма ABCD. Разложите вектор по векторам .

№4. Даны параллелограммы ABCD и A1B1CD. Докажите, что векторы компланарны.

№1. Дан правильный октаэдр EАВСDF.

а) Назовите вектор с началом в точке B,

равный .

б) Назовите вектор, равный ;

в) вектор равный .

г) Назовите вектор , удовлетворяющий

равенству .

№2. В правильном тетраэдре DABC с ребром a, точка P – центр треугольника ABC, точка Q – центр треугольника BDC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка S равноудалена от вершин треугольника ABC (). SO – перпендикуляр к плоскости ABC. Разложите вектор по векторам .

№4. Точки M и N – середины ребер BD и AC правильного тетраэдра DABC. Докажите, что векторы компланарны.

№1. Дан правильный октаэдр EАВСDF.

а) Назовите вектор с концом в точке C,

равный .

б) Назовите вектор, равный ;

в) вектор равный .

г) Назовите вектор , удовлетворяющий

равенству .

№2. В правильном тетраэдре DABC с ребром a, точка P – центр треугольника ABC, точка Q – центр треугольника BDC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка S равноудалена от сторон ромба ABCD. SO – перпендикуляр к плоскости ромба. Разложите вектор по векторам .

№4. Точки M и N – середины ребер AD и BC правильного тетраэдра DABC. Докажите, что векторы компланарны.

Контрольная работа № 5.

№1. Дан прямоугольный треугольник с гипотенузой и катетом . Отрезок , равный 12 см, – перпендикуляр к плоскости .

а) Найдите .

б) Найдите угол между прямой и плоскостью .

№2. В правильной четырехугольной пирамиде диагональ основания равна см, а двугранный угол при основании равен 60°. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение куба , проходящее через вершину и середины ребер и . Определите вид многогранника, полученного в сечении.

№1. Дан прямоугольный треугольник с катетами и . Отрезок , равный 20 см, – перпендикуляр к плоскости .

а) Найдите .

б) Найдите угол между прямой и плоскостью .

№2. В правильной четырехугольной пирамиде высота равна см, а двугранный угол при основании равен 60°. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение куба , проходящее через прямую и середину ребра . Определите вид многогранника, полученного в сечении.

№1. Диагонали ромба пересекаются в точке . – перпендикуляр к плоскости ромба. см, см, см.

а) Докажите, что прямая перпендикулярна к плоскости .

б) Найдите .

в) Найдите двугранный угол .

№2. В правильной треугольной пирамиде плоский угол при вершине равен 120°. Отрезок, соединяющий основание высоты пирамиды с серединой бокового ребра, равен 3 см. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение правильного тетраэдра , проходящее через середины ребер и параллельно ребру . Определите вид многогранника, полученного в сечении.

№1. Диагонали ромба пересекаются в точке . – перпендикуляр к плоскости ромба. см, см, см.

а) Докажите перпендикулярность плоскостей и .

б) Найдите .

в) Найдите угол между прямой и плоскостью.

№2. В правильной треугольной пирамиде двугранный угол при основании равен 60°. Отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен 3 см. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение правильного тетраэдра , проходящее через середины ребер и параллельно ребру . Определите вид многогранника, полученного в сечении.

№1. Дан равнобедренный прямоугольный треугольник с гипотенузой . – перпендикуляр к плоскости . Двугран-ный угол равен 45°.

а) Докажите перпендикулярность плоскостей и .

б) – точка пересечения медиан треугольника .

Разложите вектор по векторам .

в) Найдите углы наклона прямых и к плоскости .

№2. Основание пирамиды – прямоугольный треугольник с катетом a и противолежащим углом . Боковые грани пирамиды, содержащие данный катет и гипотенузу основания, перпендикулярны к плоскости основания, а третья боковая грань наклонена к ней под углом . Найдите площадь боковой поверхности пирамиды.

№3. Постройте сечение правильной четырехугольной пирамиды , проходящее через середины ребер основания и параллельно боковому ребру .

№1. Дан равнобедренный прямоугольный треугольник с гипотенузой . – перпендикуляр к плоскости . Прямые и образуют с плоскостью угол 30°.

а) Докажите перпендикулярность плоскостей и , если – середина .

б) – точка пересечения медиан треугольника .

Разложите вектор по векторам .

в) Найдите двугранный угол .

№2. Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковые грани пирамиды, содержащие катеты основания, перпендикулярны к плоскости основания, а третья боковая грань наклонена к ней под углом . Найдите площадь боковой поверхности пирамиды.

№3. Постройте сечение правильной четырехугольной пирамиды , проходящее через середины ребра основания и бокового ребра параллельно прямой .

📽️ Видео

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

№ 47 - Геометрия 10-11 класс АтанасянСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать

Углы с сонаправленными сторонами. Угол между прямыми. Видеоурок по геометрии 10 классСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать