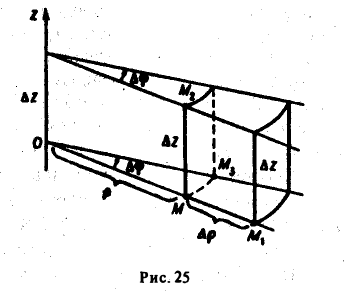
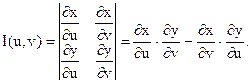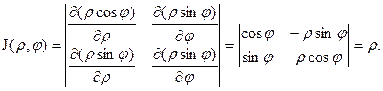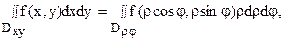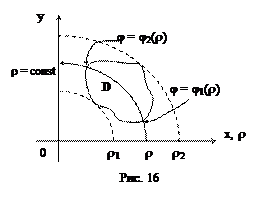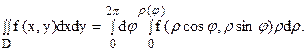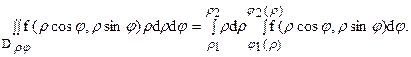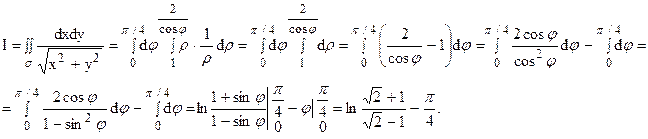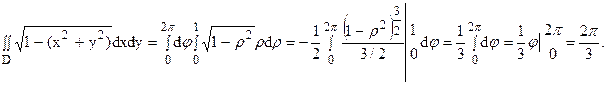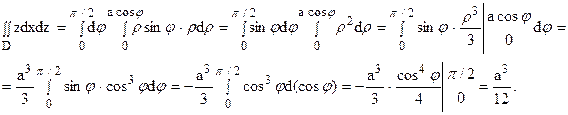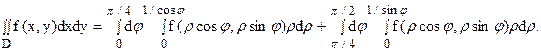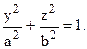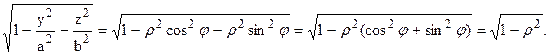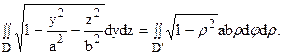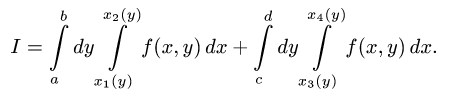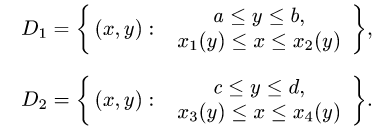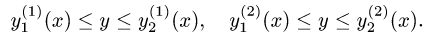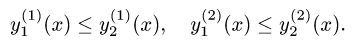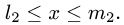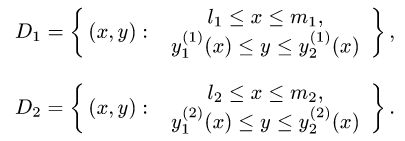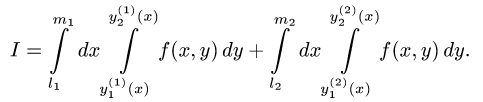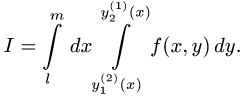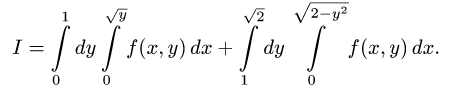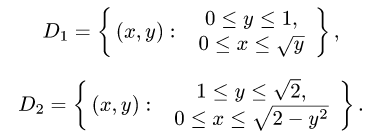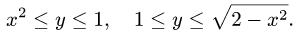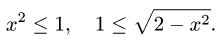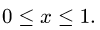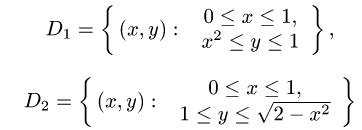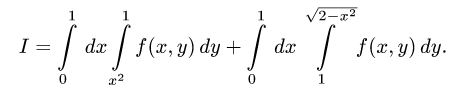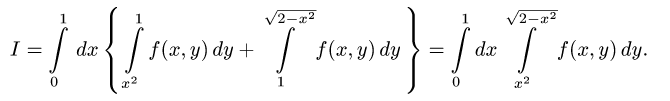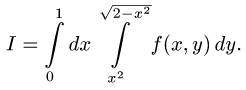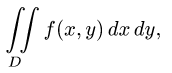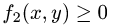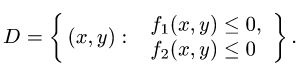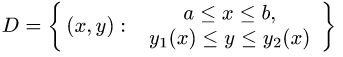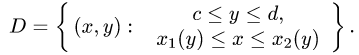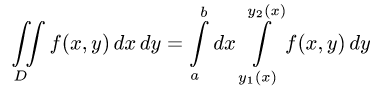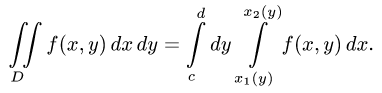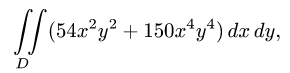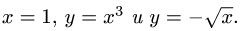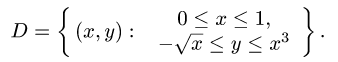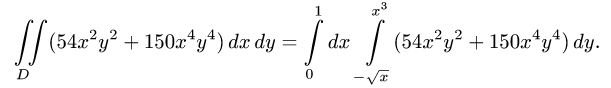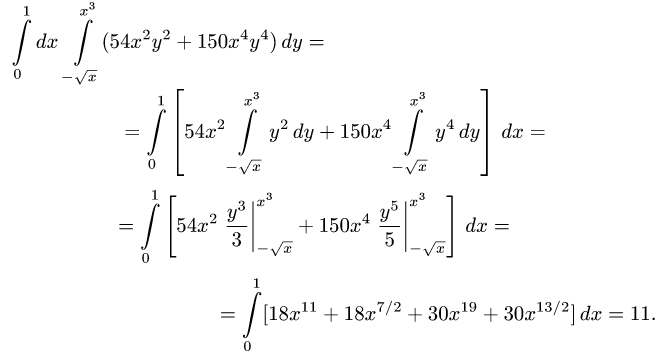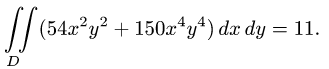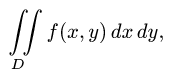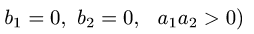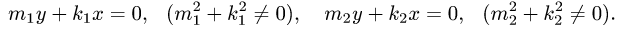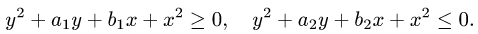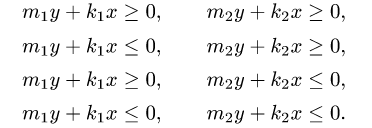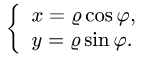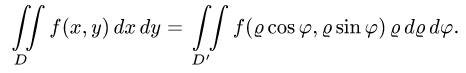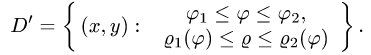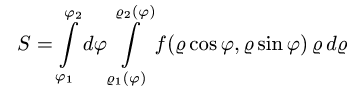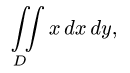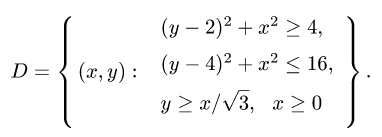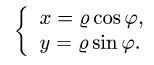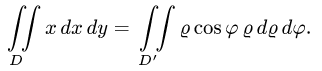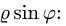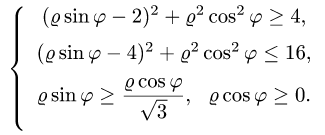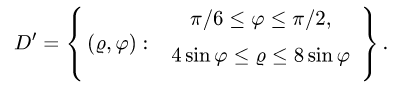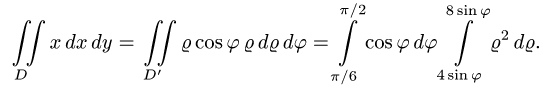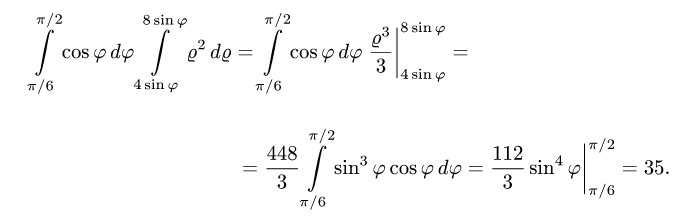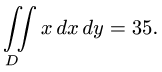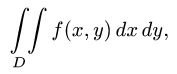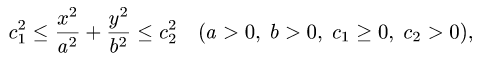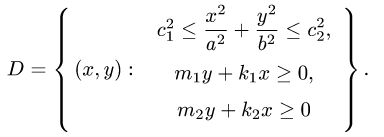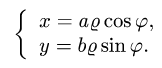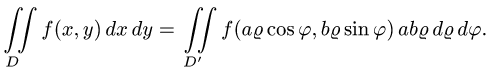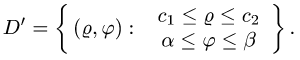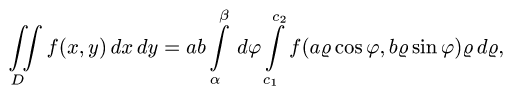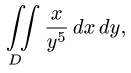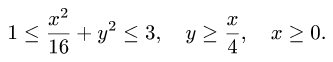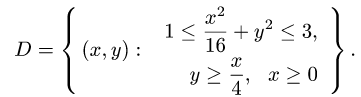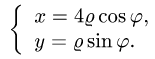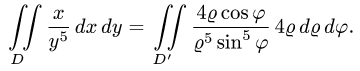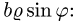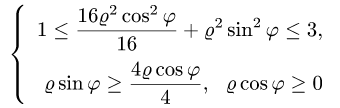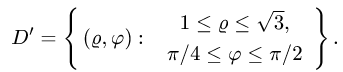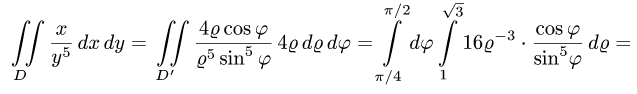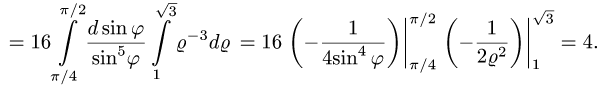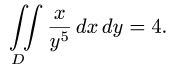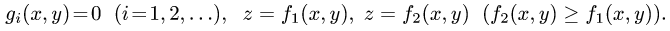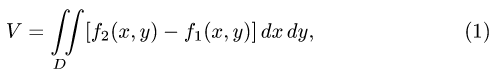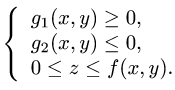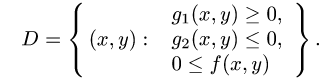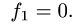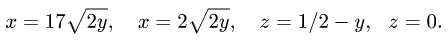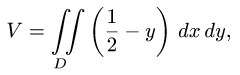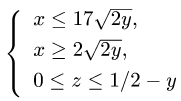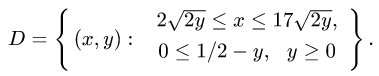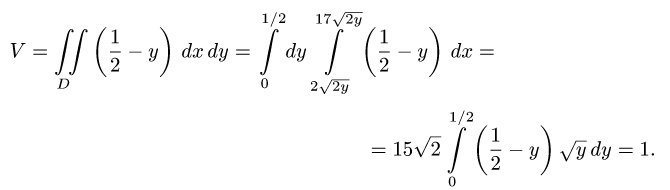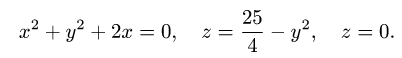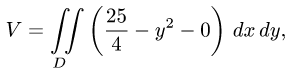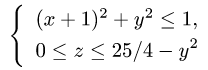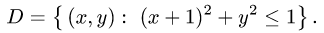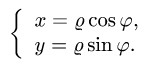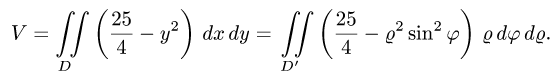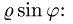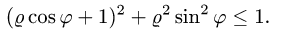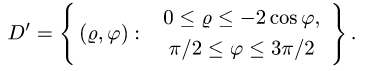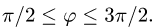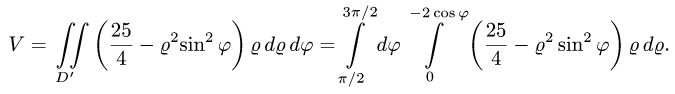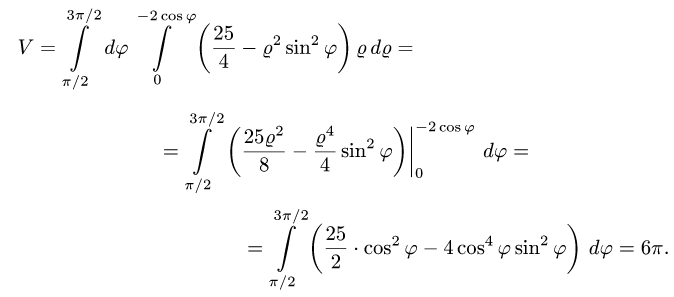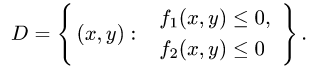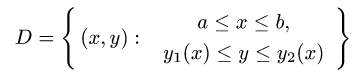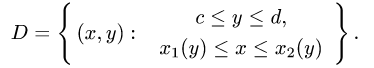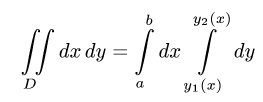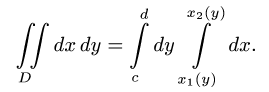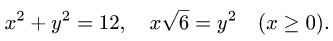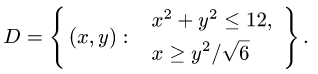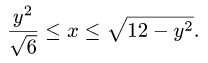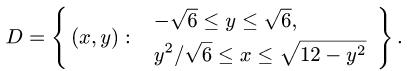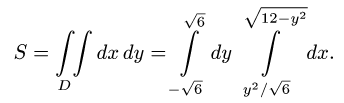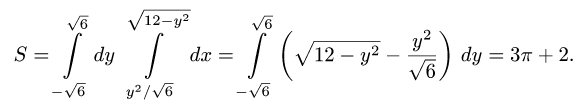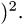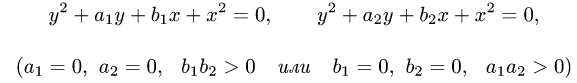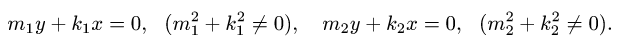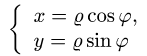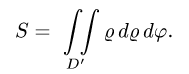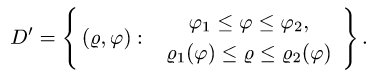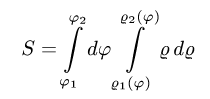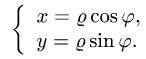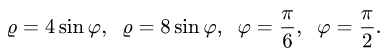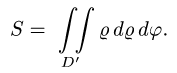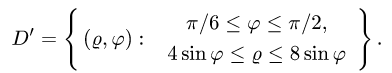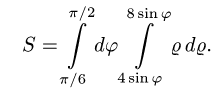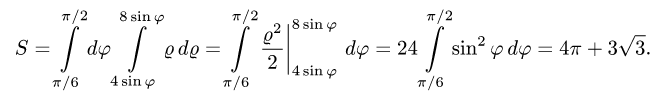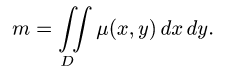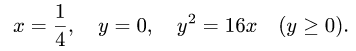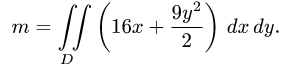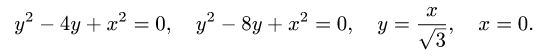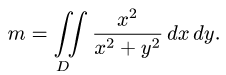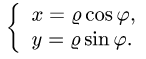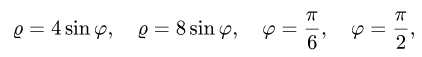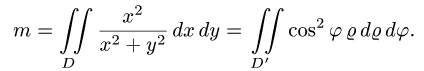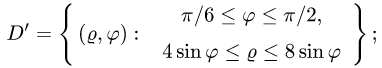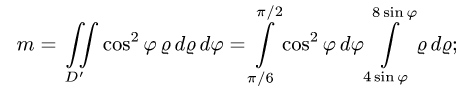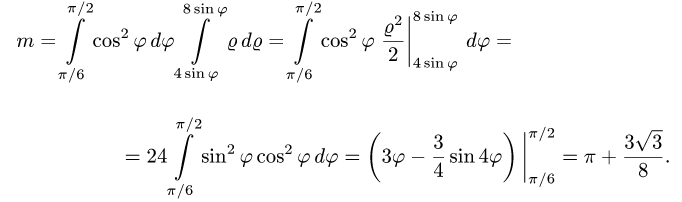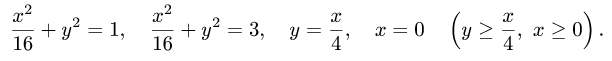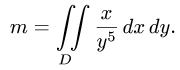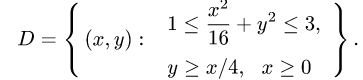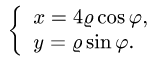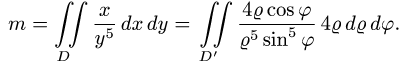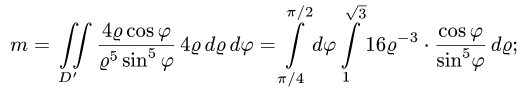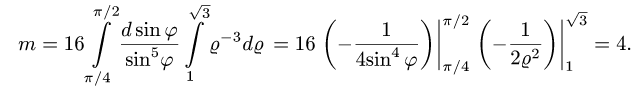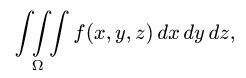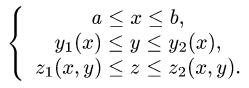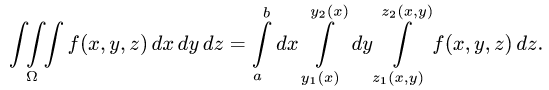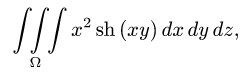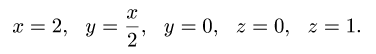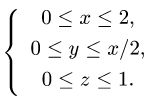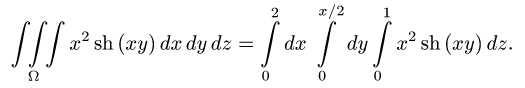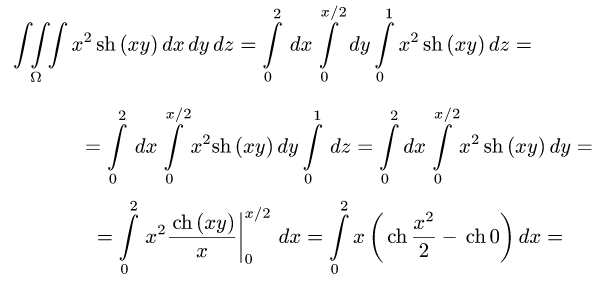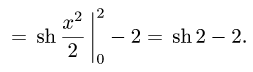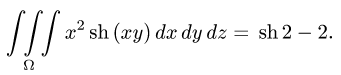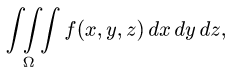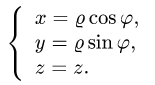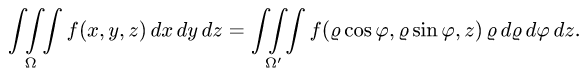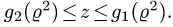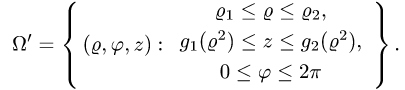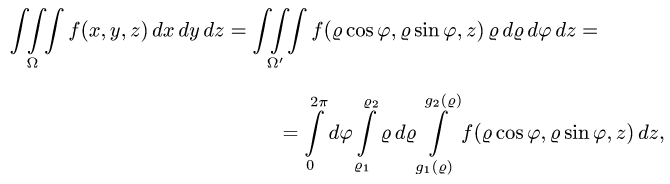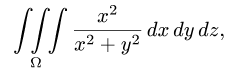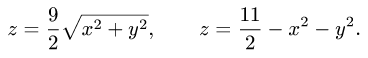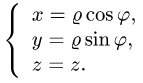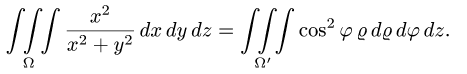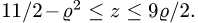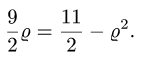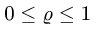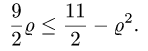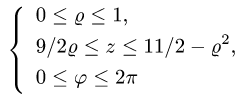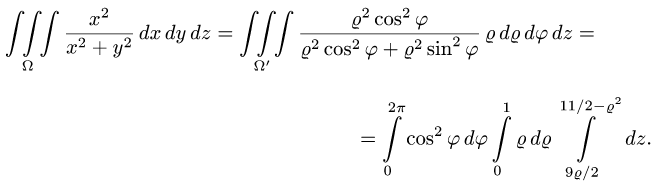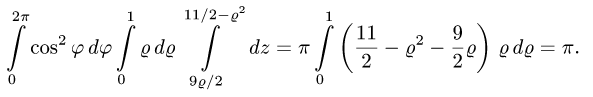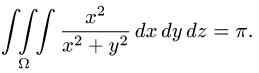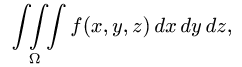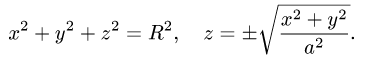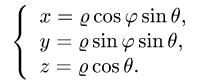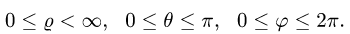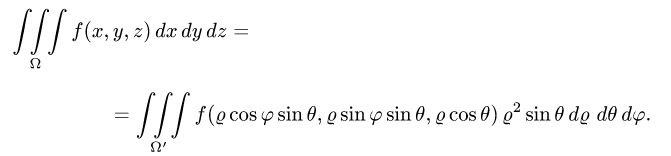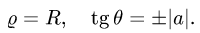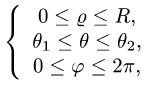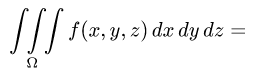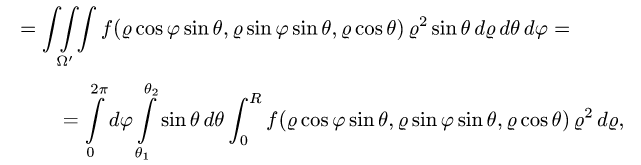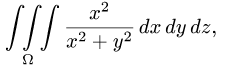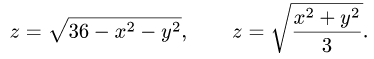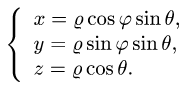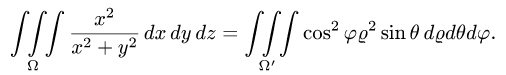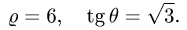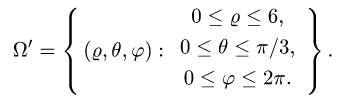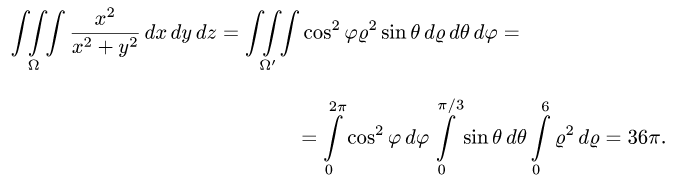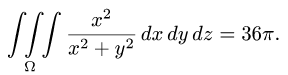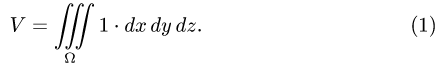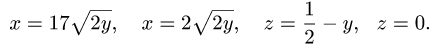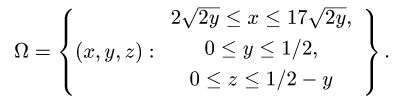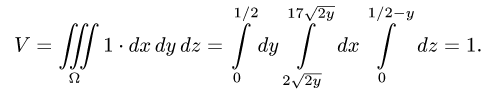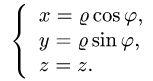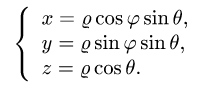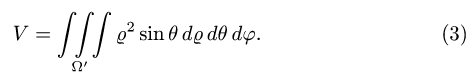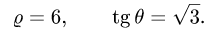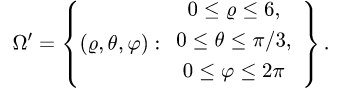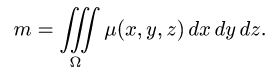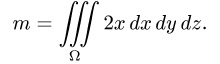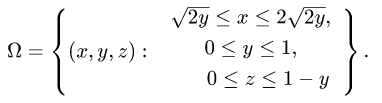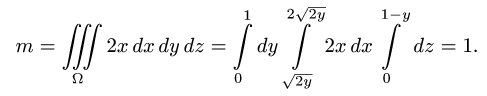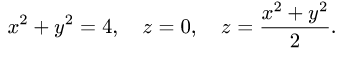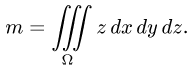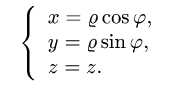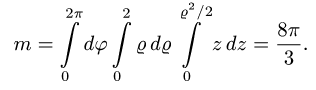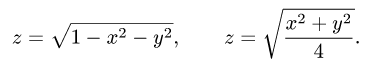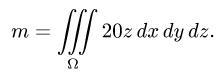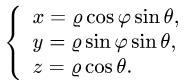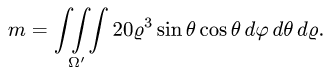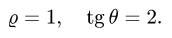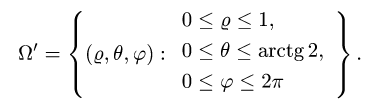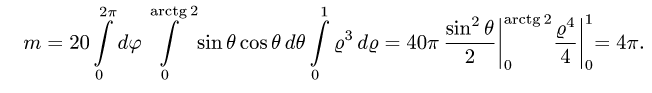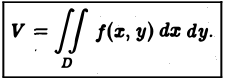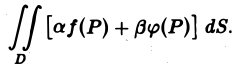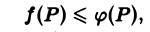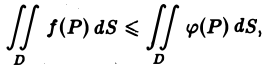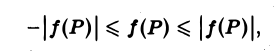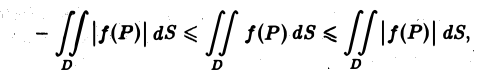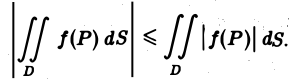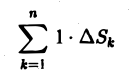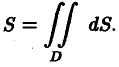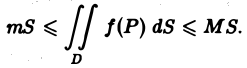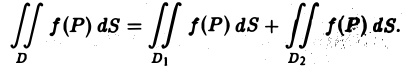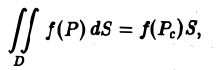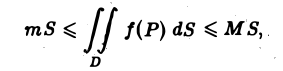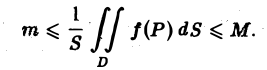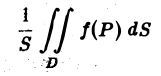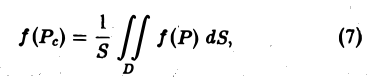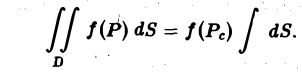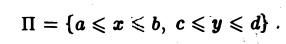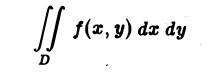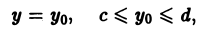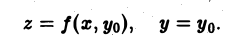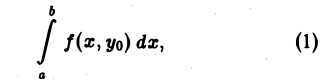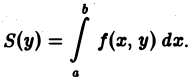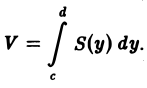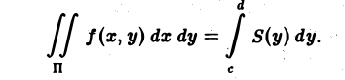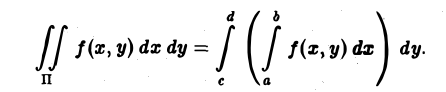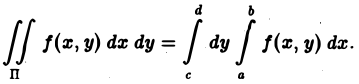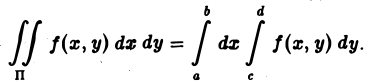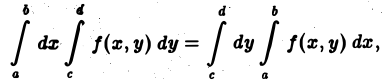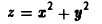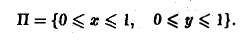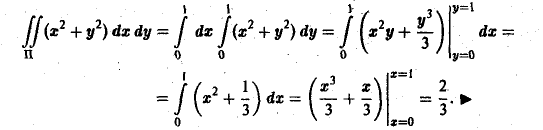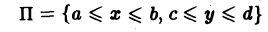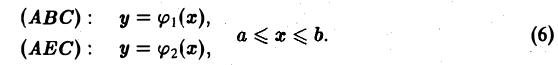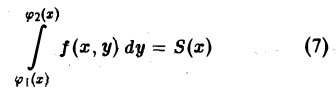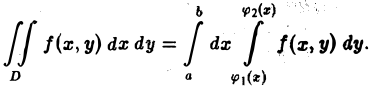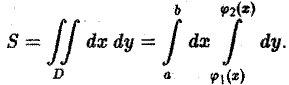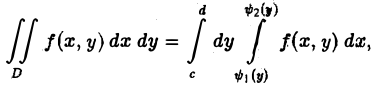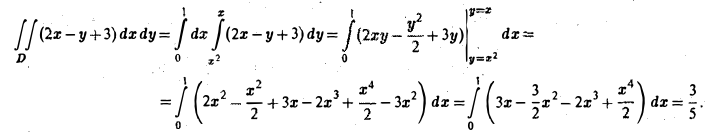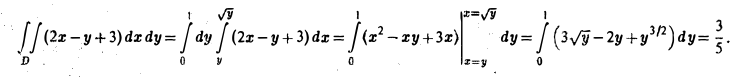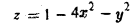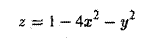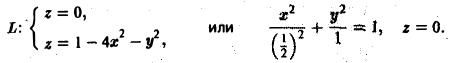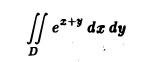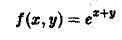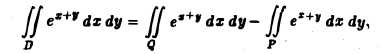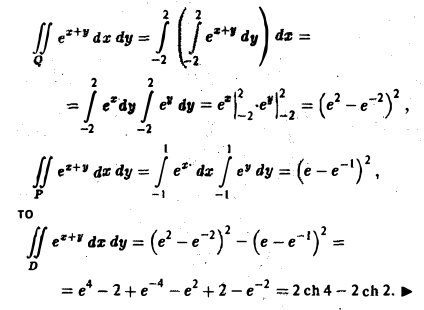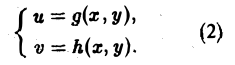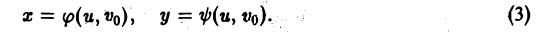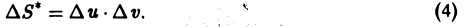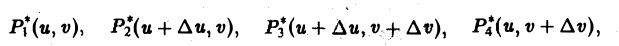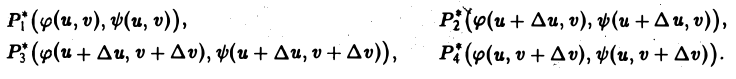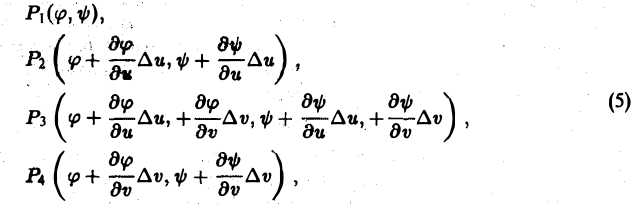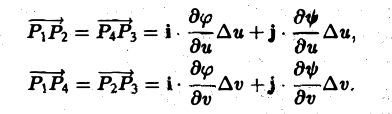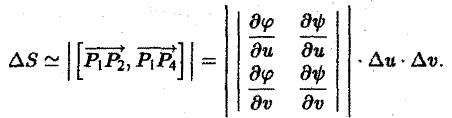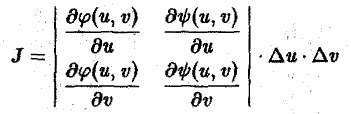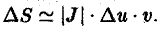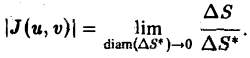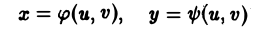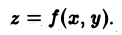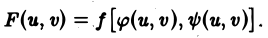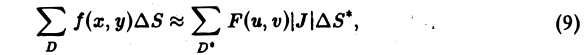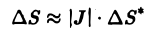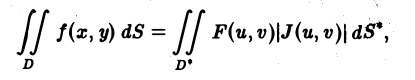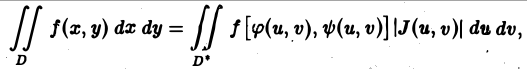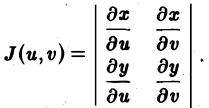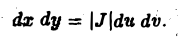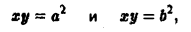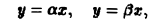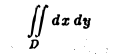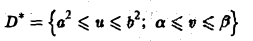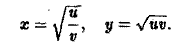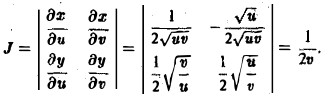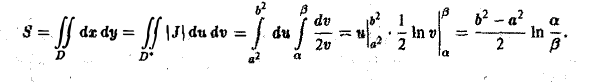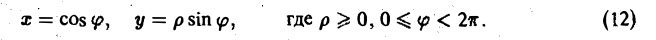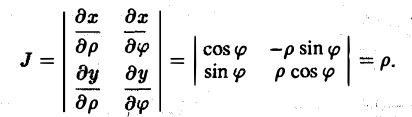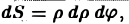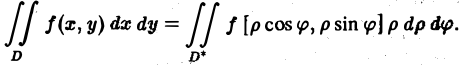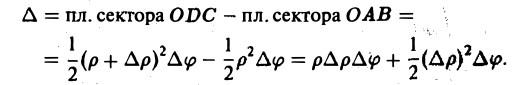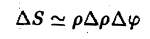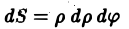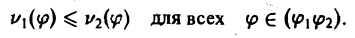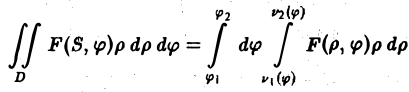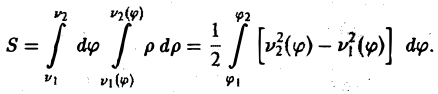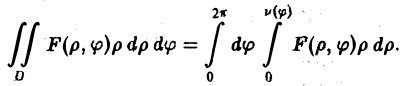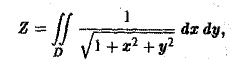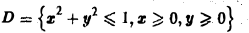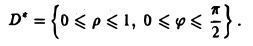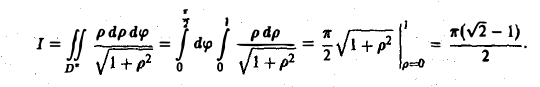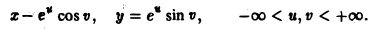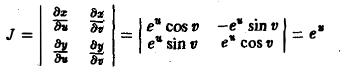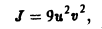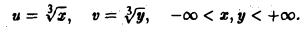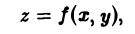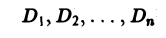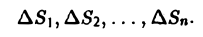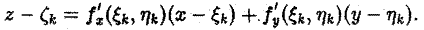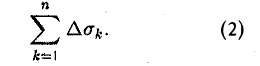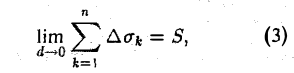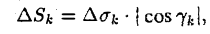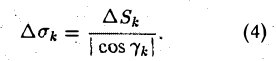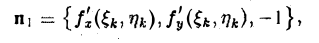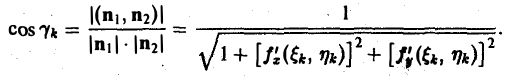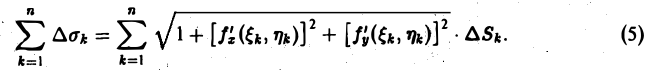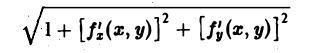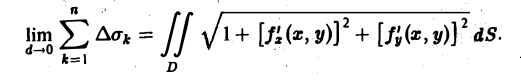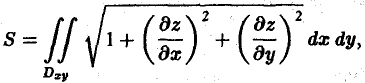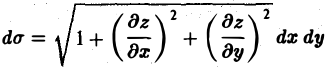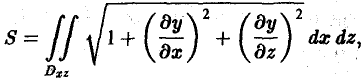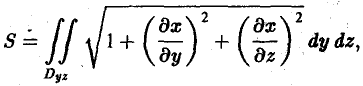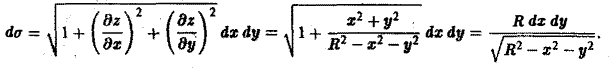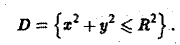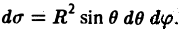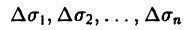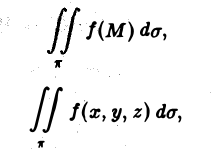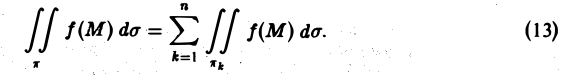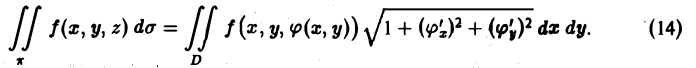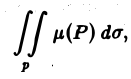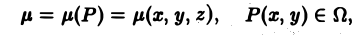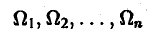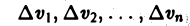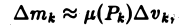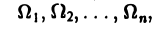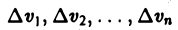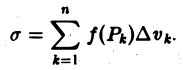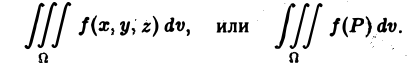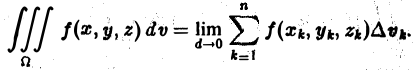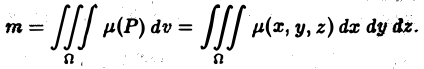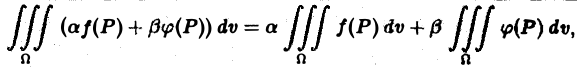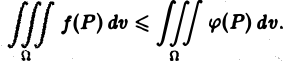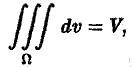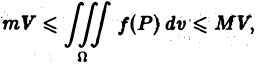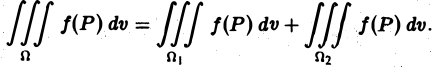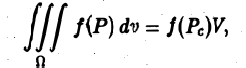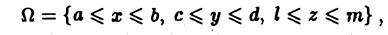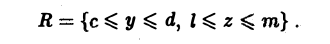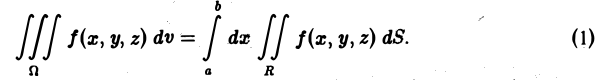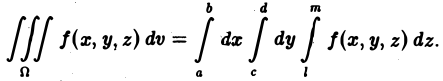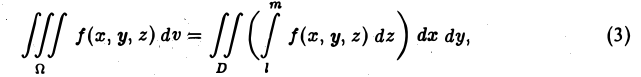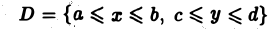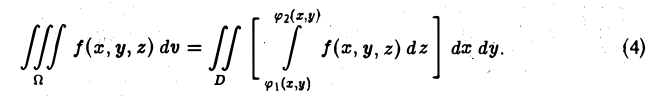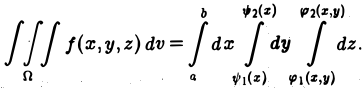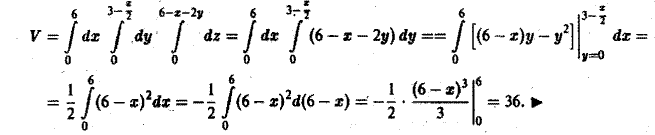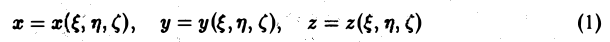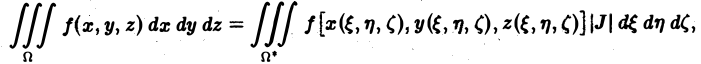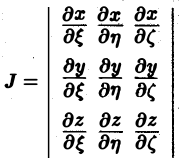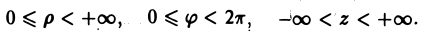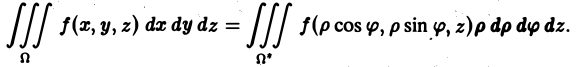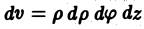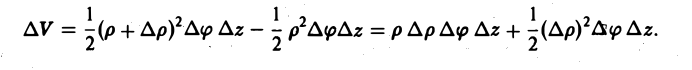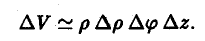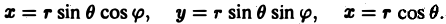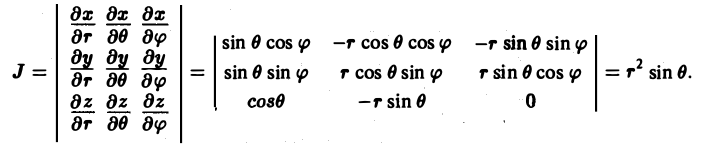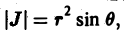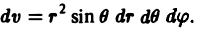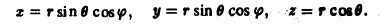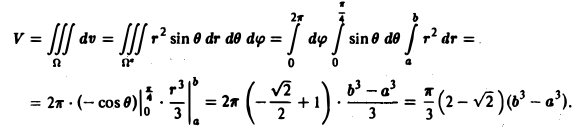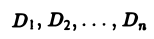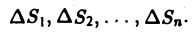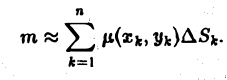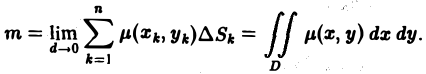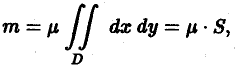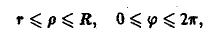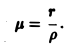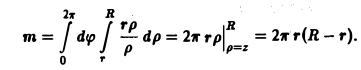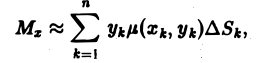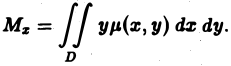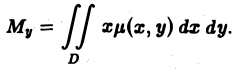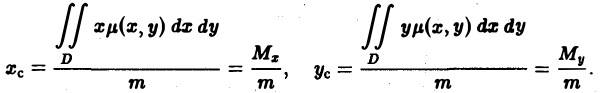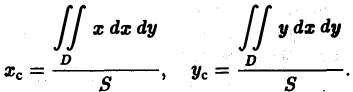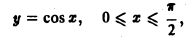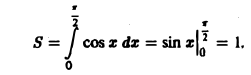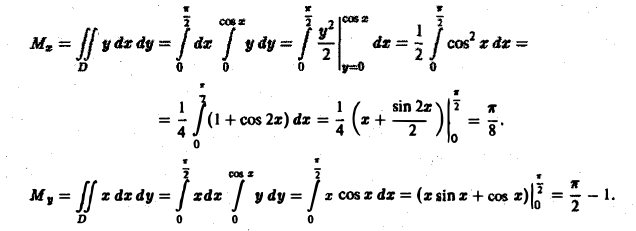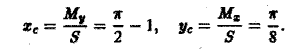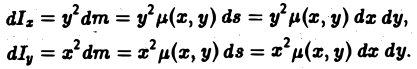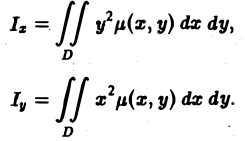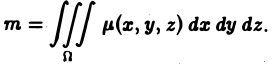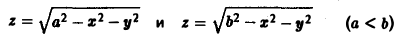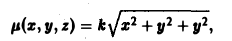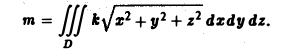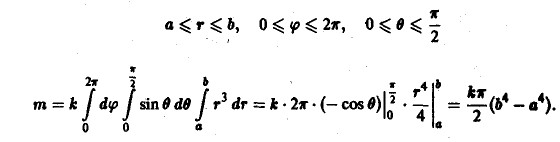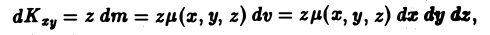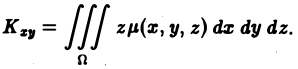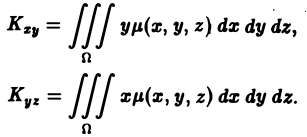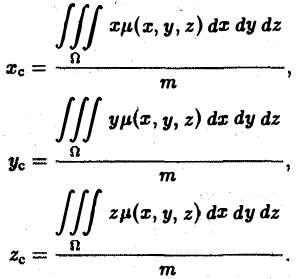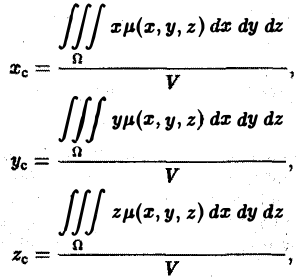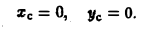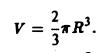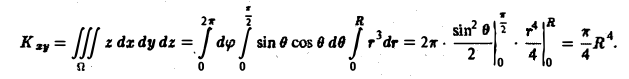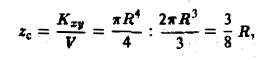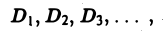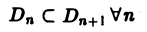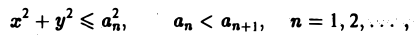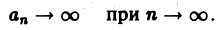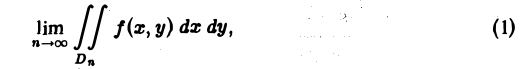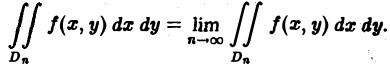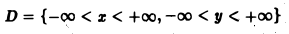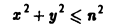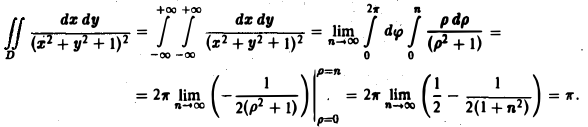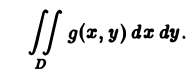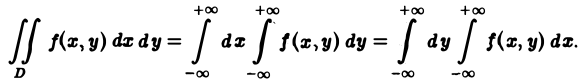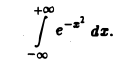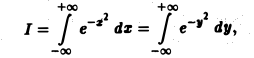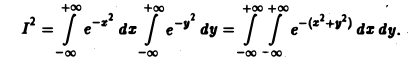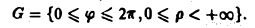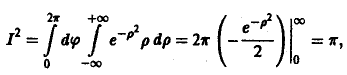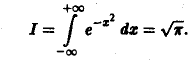- Что значит вычислить двойной интеграл?
- Сведение двойного интеграла к повторному
- Случай прямоугольной области
- Случай криволинейной или треугольной области
- Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
- x-правильная и неправильная, y-правильная и неправильная области интегрирования
- Смена порядка интегрирования
- Вычисление площади и объёма с помощью двойных интегралов
- Так что же такое двойной интеграл?
- Если область d ограничена окружностями
- Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.
- Двойные интегралы в полярных координатах: теория и примеры
- Что значит вычислить двойной интеграл в полярных координатах?
- Пределы интегрирования в повторных интегралах
- Случай первый
- Случай второй
- Случай третий
- Случай четвёртый
- Решения двойных интегралов в полярных координатах: примеры
- Приложения двойных и тройных интегралов
- Пример 3:
- Координаты центра тяжести
- Кратные интегралы в математике с примерами решения и образцами выполнения
- Изменение порядка интегрирования
- Двойной интеграл в декартовых координатах
- Двойной интеграл в полярных координатах
- Двойной интеграл в обобщенных полярных координатах
- Вычисление объемов с помощью двойного интеграла
- Вычисление площадей в декартовых координатах
- Вычисление площадей в полярных координатах
- Вычисление массы плоской пластины
- Тройной интеграл в декартовых координатах
- Тройной интеграл в цилиндрических координатах
- Тройной интеграл в сферических координатах
- Вычисление объемов с помощью тройного интеграла
- Вычисление массы тела
- Определение кратного интеграла
- Решение кратных интегралов
- Задача, приводящая к понятию двойноrо интеграла. Определение двойного интеграла
- Основные свойства двойного интеграла
- Линейное свойство
- Интегрирование неравенств
- Площадь плоской области
- Оценка интеграла
- Аддитивность
- Теорема о среднем значении
- Геометрический смысл теоремы о среднем значении
- Сведение двойного интеграла к повторному
- Случай прямоугольника
- Случай произвольной области
- Замена переменных в двойном интеграле
- Элемент площади в криволинейных координатах. Якобиан и его геометрический смысл
- Формула замены переменных в двойном интеграле
- Двойной интеграл в полярных координатах
- Площадь поверхности
- Интеграл по площади поверхности. Вычисление площади поверхности
- Интеграл по площади поверхности (интеграл по поверхности 1-го рода)
- Тройной интеграл
- Задача, приводящая к тройному интегралу
- Свойства тройных интегралов
- Теорема о среднем значении
- Вычисление тройного интеграла в декартовых координатах
- Вычисление тройного интеграла в цилиндрических и сферических координатах
- Тройной интеграл в цилиндрических координатах
- Тройной интеграл в сферических координатах
- Приложения двойных и тройных интегралов
- Масса плоской фигуры
- Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести
- Моменты инерции плоской фигуры относительно осей координат
- Вычисление массы тела
- Статические моменты тела относительно координатных плоскостей. Центр тяжести
- Понятие о несобственном кратном интеграле по неограниченной области
- 📺 Видео
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Что значит вычислить двойной интеграл?
Двойные интегралы – это обобщение понятия определённого интеграла для функции двух переменных, заданной как z = f(x, y) .
Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D .
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
Случай прямоугольной области:
Случай криволинейной области:
А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Видео:Двойной интеграл в полярных координатахСкачать

Сведение двойного интеграла к повторному
Случай прямоугольной области
Пусть дана функция двух переменных f(x, y) и ограничения для D : D = <(x; y) | a ≤ x ≤ b; c ≤ y ≤ d> , означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b , а снизу и сверху — прямые y = c и y = d . Здесь a, b, c, d — числа.
Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 1. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Пользуемся формулой 7 из таблицы интегралов. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого), пользуясь для каждого слагаемого той же формулой 7:
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области
Пусть снова дана функция двух переменных f(x, y) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b , но снизу и сверху — кривые, которые заданы уравнениями 



Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a и b — числа, а 



Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 3. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 4. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
Пример 5. Вычислить двойной интеграл

если область D ограничена прямыми

Пример 6. Вычислить двойной интеграл

если область D ограничена прямыми

Видео:Вычислить двойной интеграл, перейдя к полярным координатамСкачать

x-правильная и неправильная, y-правильная и неправильная области интегрирования
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Пример 7. Вычислить двойной интеграл 
Решение. Область интегрирования является y-неправильной, так как её нижнюю границу нельзя задать одной линией y = y(x) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части — 

Вычисляется этот двойной интеграл так:
Видео:Вычислить двойной интегралСкачать

Смена порядка интегрирования
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О’Генри: «Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки — человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же: «Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд». (О’Генри. Шехерезада с Мэдисон-сквера.)
Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 8. Сменить порядок интегрирования для повторного интеграла

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями 



Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x/2 , что видно на рисунке ниже.
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми 

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для 
Для 
Для 
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x) .
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:

Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать
Вычисление площади и объёма с помощью двойных интегралов
В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1 .
Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1 , а справа прямой y = 1 — x . (рисунок ниже).
Решая как систему уравнения этих линий, получаем точки их пересечения: 

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.
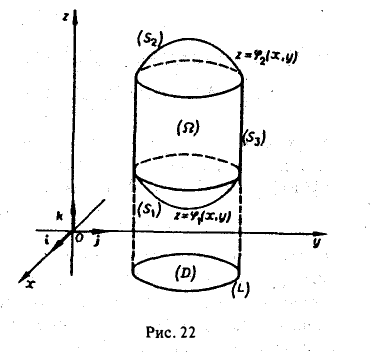
Объём криволинейного цилиндра, ограниченного сверху поверхностью 
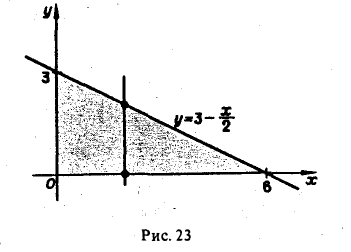
Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0 , y = 0 , z = 0 и x + y + z = 1 (рисунок ниже).
Расставляя пределы интегрирования, получаем следующий повторный интеграл:

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.
Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Так что же такое двойной интеграл?
Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями 


которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
Видео:Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Если область d ограничена окружностями
Видео:Двойной интеграл. Площадь плоской фигуры.Скачать

Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.
При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть
функции, определенные на всей плоскости xOy или в некоторой ее области Dxy и имеющие непрерывные частные производные в области Dxy. Допустим также, что систему уравнений ( 7) можно однозначно разрешить относительно x и y:
Тогда каждой точке М(x;y) из области Dxy будет взаимно однозначно соответствовать пара чисел (u,v), называемых криволинейными координатами этой точки. Если область Dxy расположена в той части плоскости xOy, в которой введены криволинейные координаты u, v, то справедлива следующая формула:
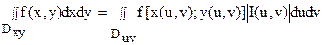
где Duv – область изменения криволинейных координат u и v, отвечающая области Dxy, а I(u,v) – якобиан преобразования ( 8):
Например, для полярных координат имеем:
В зависимости от строения области интегрирования или подынтегральной функции вычисление двойного интеграла может оказаться более простым не в прямоугольной, а в какой-нибудь из криволинейных систем координат. Наиболее распространенной из них является полярная.
Для того, чтобы преобразовать двойной интеграл в прямоугольных декартовых координатах в двойной интеграл в полярных координатах, нужно x и y в подынтегральной функции заменить соответственно через rcosj и rsinj, а выражение dxdy заменить выражением rdrdj:
где Drj – та же область Dху, но описанная в полярных координатах (поскольку в этом случае якобиан I = r).
В этой формуле следует обратить внимание на то, что в подынтегральной функции не только происходит замена координат по формулам перехода от декартовых к полярным, но и появляется дополнительный множитель r.
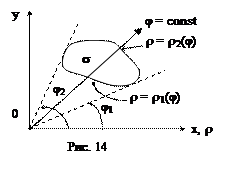
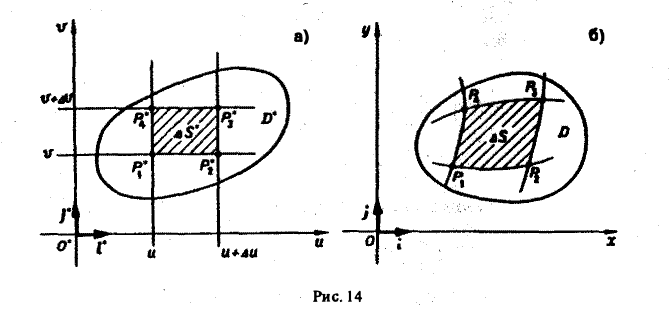
Пусть, например, внешнее интегрирование производится по j и область Dρφ является правильной в направлении j = сonst, т.е. каждый луч, выходящий из начала координат, пересекает область Dρφ по отрезку
(рис. 14).
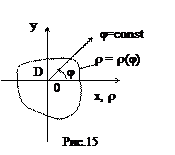
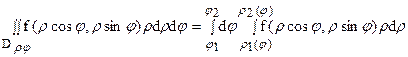
В частном случае, когда D содержит начало координат, имеем:
Если же внешнее интегрирование производится по r и область Dρφ является правильной в направлении
r = const, т.е. каждая окружность пересекает, имея центром начало координат, область Dρφ по дуге этой окружности (только в двух точках) (см. рис.16), то справедлива формула:
Пример 12.
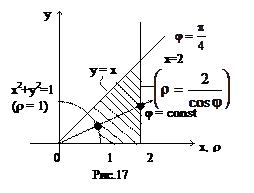
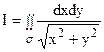
Хотя данный интеграл можно вычислить в прямоугольной декартовой системе координат, в которой он задан, но неопределенные интегралы, которые при этом возникнут, достаточно сложны.
Перейдем к полярной системе координат. Вспомним, что 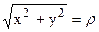
Таким образом, искомый интеграл можно представить в виде:
Пример 13.
Вычислить двойной интеграл 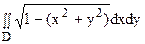
Область D есть круг радиуса 1 с центром в начале координат. Введем полярные координаты. В полярных координатах x 2 + y 2 = r 2 и уравнение окружности принимает вид r = 1.
Тогда по формуле ( 13) получаем:
Пример 14.
Вычислить двойной интеграл 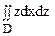
Область D – полукруг. Введем полярные координаты: x = rcosj, z = rsinj.
Уравнение окружности в полярных координатах принимает вид r 2 = racosj, или r = acosj.
Подынтегральная функция имеет вид z = rsinj. Угол j меняется от 0 до p/2 (полукруг находится в I четверти). При каждом фиксированном значении угла j r меняется от 0 (в начале координат) до r = acosj (на окружности). Тогда получаем:
Пример 15.
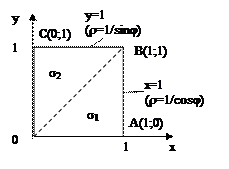
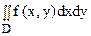
Уравнение стороны АВ (х = 1) в полярных координатах принимает вид rcosj = 1, или r = 1/cosj, а ВС будет r = 1/sinj. Угол j меняется от 0 до p/2 (квадрат находится в I четверти). При изменении угла от 0 до p/4 r меняется от 0 до r = 1/cosj, а при изменении угла от p/4 до p/2 r меняется от 0до r = 1/sinj.
Пример 16.
Вычислить двойной интеграл 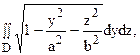
Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив y = arcosj, z = brsinj.
Найдем якобиан данного преобразования:
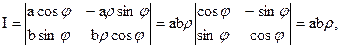
Подынтегральная функция принимает вид:
Угол j меняется от 0 до 2p. Уравнение эллипса принимает вид r = 1, поэтому r меняется от 0 до 1. И тогда
Видео:Вычисление двойного интегралаСкачать
Двойные интегралы в полярных координатах: теория и примеры
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Что значит вычислить двойной интеграл в полярных координатах?
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Видео:Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый
Полюс O находится вне области интегрирования D .
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать
Решения двойных интегралов в полярных координатах: примеры
Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 


Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 




Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности 
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности 




Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 



Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Видео:Найти площадь фигуры, ограниченной линиями. Пример 5.Скачать

Приложения двойных и тройных интегралов
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Масса плоской фигуры Пусть задана плоская ограниченная фигура D, по которой непрерывным образом распределена масса с поверхностной плотностью — функция, непрерывная в D. Разобьем фигуру D на п частей без общих внутренних точек, площади которых соответственно равны В каждой части произвольно выберем точку У к) и вычислим в ней плотность у*).
В силу непрерывности fi(x, у) можно считать, что масса т* части Dk фигуры D приближенно равна а масса всей фигуры — сумме Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей
Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Последняя является интегральной суммой для непрерывной функции ц(х> у) в области D. Переходя к пределу при d 0 (здесь d — наибольший из диаметров частичных областей получим точное равенство Если масса распределена равномерно по всей фигуре, ц = const, то формула (1) принимает вид Пример 1.
Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов г и Л, где если плотность кольца в каждой точке обратно пропорциональна расстоянию от этой точки до центра окружности и равна 1 на окружности внутреннего круга где S — площадь фигуры D.
М Фигура D задается условиями 9.2. Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести Статическим моментом Мх материальной точки массы т относительно оси Ох называется произведение ту, где у — ордината материальной точки, т. е. Здесь у может быть как положительным, так и отрицательным числом. Разбивая фигуру D на части , выбирая в каждой части Dk произвольно точку и считая, что масса этой к-й части приближенно равна и сосредоточена в точке , запишем приближенно величину статического момента фигуры D относительно оси Ох. Имеем где ASk — площадь части ) — поверхностная плотность.
Переходя к пределу при d -* 0, получаем Статический момент фигуры D относительно оси Оу находится по аналогичной формуле Если известны статические моменты Мх и Mv и масса т плоской фигуры, то координаты центра тяжести этой фигуры находятся по следующим формулам Если /1 = const, то m = /iS, где S — площадь фи гуры D, и формулы (5) принимают вид: Пример 2.
Найти центр тяжести однородн ой плоской фигуры, ограниченной косинусоидой Так как фигура — однородная, то координаты центра тяжести будем искать по фор мулам (6). Найдем сначала площадь S заданной фигуры. Имеем Затем найдем статические моменты Теперь no формулам (6) получаем Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области 9.3.
Моменты инерции плоской фигуры относительно осей координат Рассуждая аналогично изложенному выше, легко установить, что элементарные моменты инерции относительно осей Ох и Оу будут соответственно равны Интегрируя по плоской фигуре £>, получим формулы для самих моментов инерции где, как и ранее, — поверхностная плотность распределения масс. 9.4. Вычислен ие массы тела Рассматривая задачу, приводящую к тройному интегралу, мы показали, что если известна плотность распределения масс fi(x> у, г) в каждой точке некоторого тела ft, то масса этого тела вычисляется по формуле Мы предполагаем, что функция у, z) непрерывна в области П.
Возможно вам будут полезны данные страницы:
Пример 3:
Вычислить массу m тела, ограниченного полусферами и плоскостью хОу, если плотность в каждой точке пропорциональна расстоянию от этой тон ни до начала координат. 4 По условию задачи плотаостъ ц в точке (x,y,z) выражается формулой — коэффициент пропорциональности. Тогда Переходя к сферическим координатам, получим, что 9.5. Статические моменты тела относительно координатных плосюствв .
Центр тяжести Напомним, что задача о вычислении статических моментов и центра тяже сти плоской фигуры решалась при помощидвойных интегралов (см. формулы (3), (4) и (5)). Задачи о вычислении статических моментов тела ft относительно координатных плоскостей и отыскания центра тяжести тела ft решаются аналогичным способом при помощи тройных интегралов. Например, элементарный статический момент относительно плоскости хОу равен — плотность. Отсюда статический момент Аналогично выписываются статические моменты относительно плоскостей Вычислив массу m тела ft и его статические моменты, легко найти координаты центра тяжести тела:
Если тело однородно, то плотность = const и формулы (11) упрощаются — постоянный множитель /х в числителе можно вынести за знак интеграла и сократить на него числитель и знаменатель . Тогда получим 4. найти координаты центра тяжести Однородное о полуиира радиуса R. 4 Считаем, что центр шара находится в начале координат, а рассматриваемая фигура — полуша р расположена над плоскостью. Тогда в силу симметрии имеем Объем полушара равен Найдем статический момент относительно плосхости хОу: Значит, центр тяжести.
| Понятие о несобственном кратном |
интеграле по неограниченной области При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования , монотонно исчерпывающих область D, т. е. Например, если область интегрирования совпадает со всей плоскостью , то за последовательность можно принять совокупность концентрических кругов где Определение. Несобственным интегралом от функции /(ж, у) по неограниченной области интегрирования D называется предел последовательности интегралов не зависящий от выбора последовательности D„.
Итак, по определению (2) Если предел (1) существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае — расходящимся. Пример 1. Вычислить интеграл где область интегрирования — вся плоскость. м В качестве областей интегрирования выберем круги радиуса п . Переходя к полярным координатам, получим Итак, интеграл (3) сходится и равен Признак сражение.
Если ,u интеграл сходится, то сходится и интеграл Если же интеграл расходится, то расходится и интеграл Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования: 2. Вычислить интеграл 4 Так как то, согласно соотношению Переходя в двойном интеграле к полярным координатам, получим ноаую область интегрирования Следовательно, откуда Несобственные интегралы от функции трех, четырех и большего числа переменных по неограниченным областям определяются аналогично. Упражнения Вычислите двойные интегралы:
Измените порядок интегрирования (предварительно нарисовав область интегрирования): Нарисуйте область интегрирования и вычислите повторные интегралы Вычислите площади фигур, ограниченных кривыми Вычислите площадь петли кривой Вычислите площадь петли кривой Указание. Сделайте замену переменных Пугем перехода к полярным координатам вычислите следующие интегралы: если область D ограничена окружностью с центром в начале координат. — кольцо между окружностями радиусов полукруг диаметра d с центром в точке С о) , лежащий выше Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат
Координаты центра тяжести
Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Найдите массу штастиики D с заданной поверхностной плотностью Определите центры тяжести: 31. Полусегмента параболы 32. Полуэллипса отсеченного осью Ох. 33. Фигуры, ограниченной кривыми Вычислите площадь: 34.
Той части плоскости , которая лежит в первом октанте и ограничена цилиндром 35. Той части поверхности конусах которая высекается цилиндром 36. Поверхности параболоида расположенного внутри цилиндра . Вычислите интегралы по площади поверхности: 3часть плоскости , лежащая в первом октанте. где ж — часть сферы лежащая в первом октанте. — цилиндр х ограниченный плоскостями расстояние от точки ) поверхности до начала координат. Определение. Моментом инерции плоской фигуры относительно начала координат называется величина ‘ Вычислите моменты инерции относительно начала координат: 40.
Треугольника, ограниченного линиями , относительно оси Ох. 41. Треугольника с вершинами в точках относительно оси Оу. 42. Эллипса относительно оси Оу. 43. Области, ограниченной параболой у2 = 4ах, прямой Вычислите тройные интегралы: — область, ограниченная координатными плоскостями и плоскостью где ft — область, ограниченная конусом и плоско- — трехгранная призма, ограниченная плоскостя- п ми Вычислите инте1ралы 47-50, переходя к цилиндрическим или сферическим координатам: I
Вычислите объем тела, огранич енного данными поверхностями: . Указание: перейдюе к сферическим координатам. Вычислите массу тела: 54. Ограниченного поверхностями , «ели плогность ц в каждой точке тела равна аппликате этой точке. 55. Ограниченного поверхностями , если плотность/х в каждой точке равна орданате у этой точки.
Найдете статические моменты однородного тела (ц = 1): 56. Прямоугольного параллелепипеда с ребра*» а, Ь,с, относительно его граней. 57. Тела, ограниченного эллипсоидом х2 у2 z2 и плоскостью хОу, относительно плоскости хОу. Найдите координаты центра тяжести однородного тела (/* = 1), ограниченного данными поверхностями: 58. Плоскостями 59. Цилиндром и плоскостями 60. Параболоидом х2 + у2 = 2л z и полусферой .
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Семинар 4. Двойной интеграл.Скачать

Кратные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Кратные интегралы» вы научитесь записывать области (на плоскости и в пространстве) с помощью неравенств в декартовых, полярных, цилиндрических и сферических координатах, расставлять пределы интегрирования и сводить кратные
интегралы к повторным. Вы научитесь также решать задачи геометрии и механики с использованием двойных и тройных интегралов (в декартовых, полярных, обобщенных полярных, цилиндрических и сферических координатах).
Видео:Изменение порядка интегрирования в повторном интегралеСкачать

Изменение порядка интегрирования
Постановка задачи. Изменить порядок интегрирования
1.Область интегрирования состоит из двух областей 
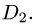
Зададим их неравенствами
2.Решаем системы неравенств, определяющих области 
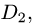
относительно у и получаем
3.Определяем границы изменения х, решая неравенства
Получаем 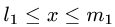
4.Области 
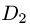
5.Записываем интегралы I с измененным порядком интегрирования:
6.Если 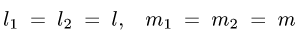
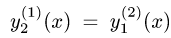
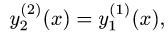
то I можно представить одним интегралом
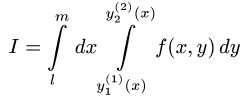
Пример:
Изменить порядок интегрирования
Решение:
1.Область интегрирования состоит из двух областей 
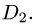
Зададим их неравенствами
2.Решаем системы неравенств, определяющих области 
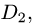
относительно у и получаем
3.Определяем границы изменения х, решая неравенства
Учитывая, что 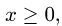
4.Области 
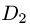
5.Записываем интегралы I с измененным порядком интегрирования:
6.Пользуясь линейностью и аддитивностью интегралов, получаем
Ответ.
Двойной интеграл в декартовых координатах
Постановка задачи. Вычислить двойной интеграл
где область D ограничена линиями 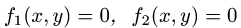
1.Зададим область D неравенствами. Для этого выясним, каким
из неравенств
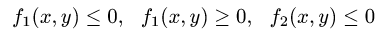
удовлетворяют координаты точек области D.
Пусть, например, такими неравенствами оказались 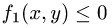
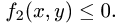
Решаем неравенства, определяющие D, относительно х и у. Получаем
2.Переходим от двойного интеграла к повторному:
3.Последовательно интегрируем, используя свойства определенного интеграла.
Замечание:
Если необходимо, разбиваем область на части и используем свойство аддитивности интеграла.
Пример:
Вычислить двойной интеграл
где область D ограничена линиями
Решение:
1.Зададим область D неравенствами. Очевидно, что 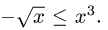
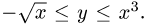
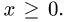
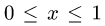
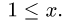
2.Переходим от двойного интеграла к повторному:
3.Используя свойства определенного интеграла, последовательно
интегрируем сначала по у (считая х постоянной), затем по х:
Ответ.
Двойной интеграл в полярных координатах
Постановка задачи. Вычислить двойной интеграл
где область D ограничена двумя окружностями
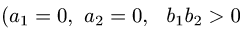
и двумя прямыми
1.Зададим область D неравенствами в декартовой системе координат.
Для этого заметим, что окружности 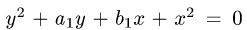
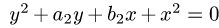
расположены на оси ОХ (при 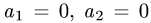
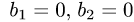
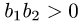
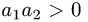
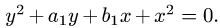
Прямые 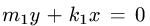
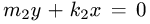
координат. Область D расположена между ними. Учитывая, в какой полуплоскости находятся окружности и, следовательно, область
D, определяем, каким из следующих пар неравенств удовлетворяют
координаты точек области D:
2.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
При этом 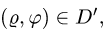
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на 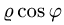
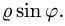
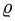
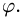
4.Переходим от двойного интеграла к повторному:
и последовательно интегрируем, используя свойства определенного
интеграла.
Пример:
Вычислить двойной интеграл
где область D ограничена линиями
Решение:
1.Зададим область D неравенствами в декартовой системе координат. Для этого заметим, что, выделяя полные квадраты в уравнениях окружностей 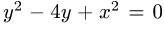
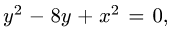
привести к виду
Очевидно, что обе окружности проходят через начало координат
и их центры расположены на оси OY в точках (0,2) и (0,4). Окружность (1) имеет радиус 2 и, следовательно, лежит внутри окружности (2), имеющей радиус 4. Поскольку область D находится между окружностями, координаты ее точек удовлетворяют неравенствам
Прямые 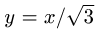
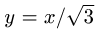
2.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
При этом 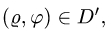
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на 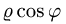
Решая эти неравенства относительно 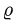
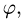
4.Переходим от двойного интеграла к повторному:
Последовательно интегрируя, получаем
Ответ.
Двойной интеграл в обобщенных полярных координатах
Постановка задачи. Вычислить двойной интеграл
где область D задана неравенствами
1.Область D задана неравенствами в декартовой системе координат, т.е.
2.Так как область D ограничена эллипсами и прямыми, проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
При этом 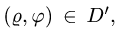
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на 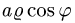
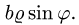
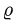
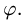
4.Переходим от двойного интеграла к повторному:
и последовательно интегрируем, используя свойства определенного
интеграла.
Пример:
Вычислить двойной интеграл
где область D задана неравенствами
Решение:
1.Область D задана неравенствами в декартовой системе координат:
2.Так как область D ограничена эллипсами и прямыми, проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
При этом 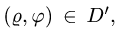
3.Чтобы найти область D’, заменяем в неравенствах, определяющих область D, х на 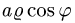
Решая эти неравенства относительно 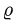
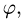
4.Переходя от двойного интеграла к повторному и последовательно интегрируя, получаем
Ответ.
Вычисление объемов с помощью двойного интеграла
Постановка задачи. Найти объем тела, ограниченного поверхностями
1.Объем цилиндрического бруса, ограниченного заданными поверхностями, определяется формулой
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z.
Допустим, например, что координаты точек тела удовлетворяют
неравенствам 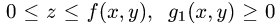
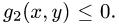
Исключая z, получим
3.Вычисляем двойной интеграл по формуле (1) при 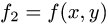
Записываем ответ, не забывая о размерности.
Пример:
Найти объем тела, ограниченного поверхностями
Решение:
1.По формуле (1) с 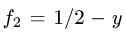
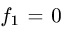
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z. В данном случае тело определяется системой неравенств
Здесь неравенство 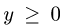
квадратного корня.
3.Вычисляем двойной интеграл:
Ответ. V = 1 ед. объема.
Пример:
Найти объем тела, ограниченного поверхностями
Решение:
1.По формуле (1) с 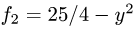
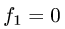
где D — проекция тела на плоскость XOY.
2.Чтобы найти D, задаем тело с помощью неравенств и исключаем из них z. В данном случае тело определяется неравенствами
Из первого неравенства очевидно, что 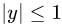
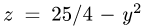
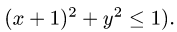
3.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
При этом 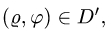
4.Чтобы найти область 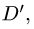
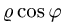
Заметим, что из неравенств 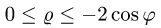
5.Переходим от двойного интеграла к повторному:
Последовательно интегрируя, получаем
Ответ. 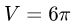
Вычисление площадей в декартовых координатах
Постановка задачи. Найти площадь области D, ограниченной
линиями 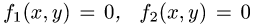
х = b или у = с и у = d).
План решения.
Из определения двойного интеграла следует, что искомая площадь
S численно равна
1.Зададим область D неравенствами. Для этого выясним, какие
из неравенств 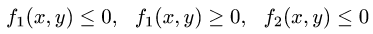
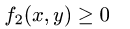
выполняются для координат точек области D.
Пусть, например, такими неравенствами оказались 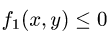
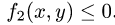
Решаем неравенства, определяющие D, относительно х и у. Получаем
2.Переходим от двойного интеграла к повторному:
3.Последовательно интегрируем, используя свойства определенного интеграла.
Записываем ответ, не забывая о размерности.
Замечание:
Если необходимо, разбиваем область на части и используем свойство аддитивности интеграла.
Пример:
Найти площадь области D, ограниченной линиями
Решение:
1.Зададим область D неравенствами. Область не может находиться вне круга, так как тогда она неограничена. Область не может
находиться слева от параболы, так как в этом случае ее точки могут
иметь отрицательные абсциссы, что исключено условием 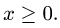
Следовательно,
Решаем неравенства, определяющие D, относительно х и у. Получаем
Следовательно, 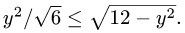
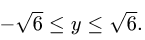
2.Вычисляем площадь области D по формуле (1). Переходя от
двойного интеграла к повторному, получим
3.Используя свойства определенного интеграла, последовательно
интегрируем:
Ответ. 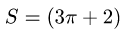
Вычисление площадей в полярных координатах
Постановка задачи. Найти площадь области D, ограниченной
двумя окружностями
и двумя прямыми
План решения. Из определения двойного интеграла следует, что
искомая площадь S численно равна
1.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать, переходя к полярным координатам
и записывая уравнения границ в полярных координатах.
При этом область D перейдет в область D’, а искомая площадь
будет равна
2.Зададим неравенствами область D’ в полярных координатах:
3.Переходим от двойного интеграла к повторному:
и вычисляем его, пользуясь свойствами определенного интеграла.
Записываем ответ, не забывая о размерности.
Пример:
Найти площадь фигуры, ограниченной данными линиями
Решение:
1.Так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать, переходя к полярным координатам
При этом область D перейдет в область D’, ограниченную линиями
А искомая площадь будет равна
2.Зададим неравенствами область D’ в полярных координатах:
3.Переходим от двойного интеграла к повторному:
Последовательно интегрируя, получим
Ответ. 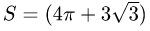
Вычисление массы плоской пластины
Постановка задачи. Найти массу плоской пластины D с поверхностной плотностью 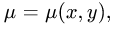
1.Масса пластины D с поверхностной плотностью 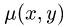
2.Вычисляем полученный двойной интеграл. Записываем ответ,
не забывая о размерности.
Пример:
Найти массу пластины D с поверхностной плотностью 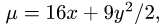
Решение:
1. Масса пластины D с поверхностной плотностью 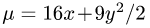
определяется формулой
2.Вычисляем полученный двойной интеграл в декартовых координатах:
а) зададим область D системой неравенств:
Неравенство 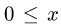
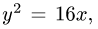
б) перейдем от двойного интеграла к повторному:
в) последовательно интегрируем, используя свойства определенного интеграла:
Ответ. m = 2 ед. массы.
Пример:Найти массу пластины D с поверхностной плотностью
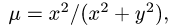
Решение:
1.Масса пластины D с поверхностной плотностью 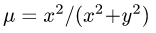
определяется формулой
2.Вычисляем полученный двойной интеграл:
а) так как область D ограничена окружностями и прямыми, проходящими через начало координат, поставленную задачу проще решать в полярных координатах
При этом область D перейдет в область D’, ограниченную линиями
а искомая масса определяется формулой
Зададим неравенствами область D’ в полярных координатах:
б) перейдем от двойного интеграла к повторному
последовательно интегрируя, получим
Ответ. 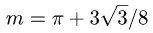
Пример:
Найти массу пластины D с поверхностной плотностью
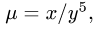
Решение:
1.Масса пластины D с поверхностной плотностью 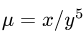
2.Вычисляем полученный двойной интеграл:
а) зададим область D неравенствами в декартовой системе координат
Так как область D ограничена эллипсами и прямыми, проходящими
через начало координат, поставленную задачу проще решать в обобщенных полярных координатах
При этом 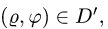
Чтобы найти область D’, заменяем в неравенствах, определяющих
область D, х на 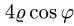
Решая эти неравенства относительно 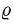
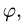
б) переходим от двойного интеграла к повторному:
в) последовательно интегрируя, получаем
Ответ. m = 4 ед. массы.
Тройной интеграл в декартовых координатах
Постановка задачи. Вычислить тройной интеграл
где область 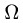
1.Зададим область 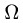
2.Перейдем от тройного интеграла к повторному:
Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая хну постоянными), затем по у
(считая х постоянной), затем по х.
Пример:
Вычислить тройной интеграл
где 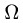
Решение:
1.Зададим область 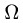
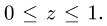
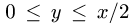
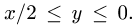
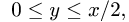
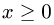
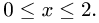
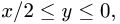
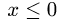
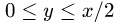
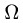
2.Перейдем от тройного интеграла к повторному:
3.Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая хну постоянными), затем по у
(считая х постоянной), затем по х:
Ответ.
Тройной интеграл в цилиндрических координатах
Постановка задачи. Вычислить тройной интеграл
где область 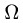
1.Поскольку 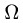
к цилиндрическим координатам
При этом 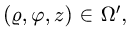
2.Зададим область 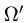
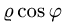
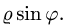
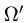
определяется неравенствами 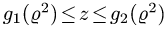
Чтобы выбрать правильные неравенства, решаем уравнение 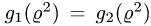
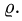
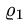
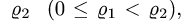
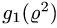
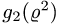
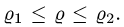
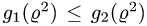
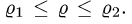
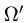
Если уравнение 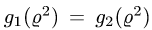
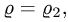
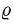
3.Переходим от тройного интеграла к повторному:
и последовательно интегрируем, используя свойства определенного
интеграла.
Пример:
Вычислить тройной интеграл
где область 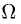
Решение:
1.Поскольку 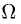
к цилиндрическим координатам
При этом 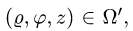
2.Зададим область 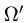
в уравнениях поверхностей х на 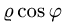
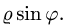
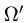
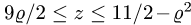
Чтобы выбрать правильные неравенства, решаем уравнение
Это уравнение имеет единственное положительное решение 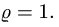
Следовательно, 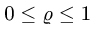
Таким образом, область 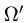
3.Переходим от тройного интеграла к повторному:
Последовательно интегрируя, получаем
Ответ.
Тройной интеграл в сферических координатах
Постановка задачи. Вычислить тройной интеграл
где область 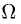
1.Поскольку 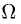
перейти к сферическим координатам
Возможные границы изменения сферических координат суть
При этом 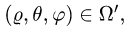
2.Заменяем в уравнениях поверхностей х на 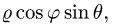
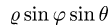
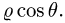
3.Зададим область 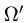
где границы изменения 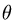
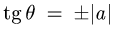
учитывая, что 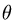
Замечание. Если 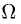
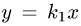
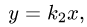
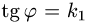
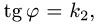
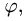
4.Переходим от тройного интеграла к повторному:
и последовательно интегрируем, используя свойства определенного
интеграла.
Пример:
Вычислить тройной интеграл
где область 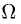
Решение:
1.Поскольку 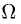
верхним полуконусом, удобно перейти к сферическим координатам
При этом 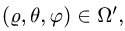
2.Заменяем в уравнениях поверхностей x на 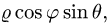
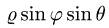
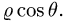
3.Зададим область 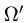
4.Переходя от тройного интеграла к повторному и последовательно интегрируя, получаем
Ответ.
Вычисление объемов с помощью тройного интеграла
Постановка задачи. Найти объем тела 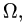
План решения. Искомый объем равен
1.Зададим область 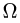
2.Вычисляем тройной интеграл, сводя его к повторному, и записываем ответ, не забывая о размерности.
Пример:
Найти объем тела 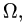
Решение:
1.Зададим область 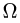
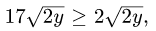
для х имеем неравенства 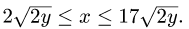
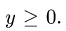
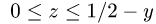
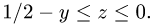
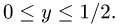
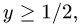
2.Вычисляем объем по формуле (1), сводя тройной интеграл к
повторному:
Ответ. V = 1 ед. объема.
Пример:
Найти объем тела 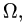
Решение:
1.Поскольку 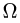
При этом 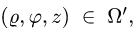
где область 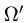
2.Зададим область 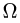
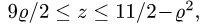
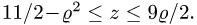
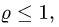
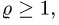
3.Вычисляем объем по формуле (2), сводя тройной интеграл к
повторному:
Ответ. 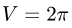
Пример:
Найти объем тела 
Решение:
1.Поскольку 
верхним полуконусом, удобно перейти к сферическим координатам
При этом 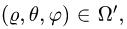
Заменяем в уравнениях поверхностей х на 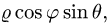
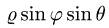
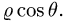
Область 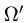
2.Зададим область 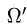
3.Вычисляем объем по формуле (3), сводя тройной интеграл к
повторному:
Ответ. 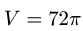
Вычисление массы тела
Постановка задачи. Найти массу тела 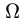
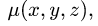
1.Масса тела 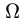
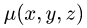
2.Зададим область 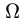
3.Вычисляем тройной интеграл, сводя его к повторному, и записываем ответ, не забывая о размерности.
Пример:
Найти массу тела 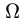
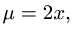
Решение:
1.Масса тела 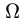
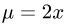
2.Зададим область 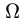
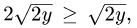
для х имеем неравенства 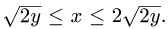
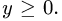
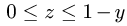
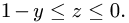
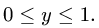
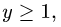
3.Вычисляем m, сводя тройной интеграл к повторному:
Ответ. m = 1 ед. массы.
Пример:
Найти массу тела 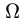
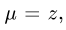
Решение:
1.Масса тела 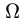
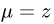
Поскольку 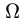
цилиндрическим координатам
При этом 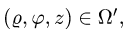
Заменяем в уравнениях поверхностей х на 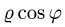
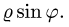
2.Зададим область 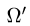
3.Вычисляем m, сводя тройной интеграл к повторному:
Ответ. 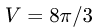
Пример:
Найти массу тела 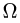
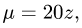
Решение:
1.Масса тела 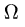
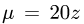
Поскольку 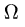
При этом 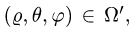
Заменяем в уравнениях поверхностей х на 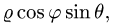
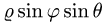
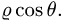
Область 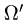
2.Зададим область 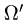
3.Вычисляем m, сводя тройной интеграл к повторному:
Здесь мы воспользовались формулой
Ответ.
Видео:Как расставить пределы интегрирования в двойном интегралеСкачать
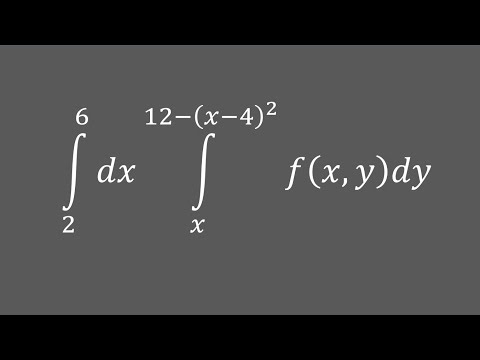
Определение кратного интеграла





Глава 26
Видео:Двойной интеграл по прямоугольной областиСкачать

Решение кратных интегралов
Задача, приводящая к понятию двойноrо интеграла. Определение двойного интеграла
К понятию двойного интеграла мы приходим, решая конкретную задачу вычисления объема цилиндрического тела.
Цилиндрическим телом называется тело, ограниченное плоскостью 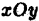
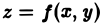
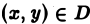
Область 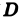
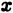
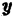
При определении объема тела будем исходить из двух принципов:
1)если разбить тело на части, то его объем, равен сумме объемов всех частей (свойство аддитивности);
2) объем прямого цилиндра, ограниченного плоскостью 
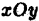
В дальнейшем мы будем предполагать, что область D является связной (состоящей из одного куска), квадрируемой (т. е. имеющей площадь) и ограниченной (т. е. расположенной внутри некоторого круга с центром в начале координат) .
Пусть 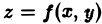
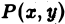
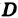
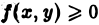
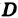
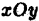
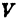
Разобъём область 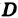
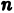
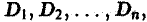
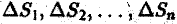
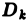
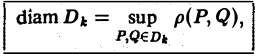
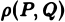
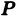
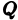
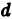
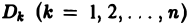
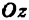
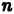
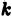
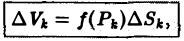
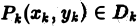
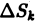
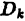
Проделав описанные построения для каждого частичного цилиндрического тела:, получим 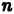
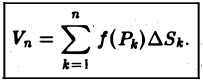
Интуитивно ясно, 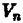
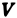
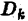
Принимаем объем 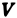
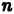
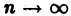
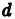
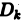
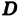
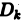
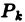
Пусть 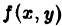
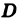
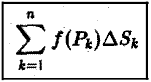
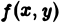
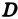
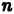
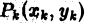
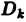
Определение:
Если nри 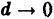
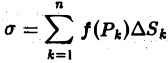
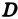
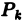
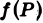
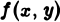
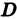
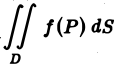
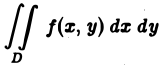
Итак, 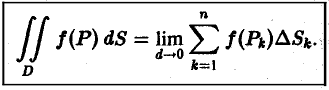
Сама функция 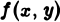
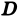
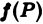
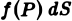
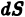
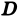
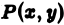
Возвращаясь к цилиндрическому телу, заключаем: объем цилиндрического тела, ограниченного плоскостью 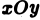
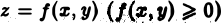
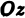
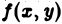
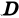
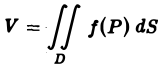
Здесь 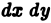
Если 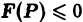
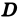
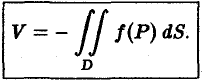
Если в области 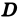
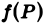
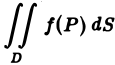
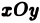
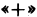
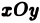
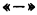
К составлению сумм вида (l) для функции двух независимых переменных и к последующему переходу приводят самые разнообразные задачи, а не только задача об объеме цилиндрического тела.
Сформулируем достаточные условия интегрируемости.
Теорема:
Всякая функция 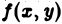
Требование непрерывности подынтегральной функции часто оказывается слишком стеснительным. Для приложений важна следующая теорема, гарантирующая существование двойного интеграла для некоторого класса разрывных функций.
Будем говорить, что некоторое множество точек плоскости, имеет площадь нуль, если ero можно заключить в многоугольную фигуру сколь угодно малой площади.
Теорема:
Если функция 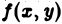
Основные свойства двойного интеграла
Двойные интегралы обладают рядом свойств, аналогичных свойствам определенного интеграла для функций одной независимой переменной.
Линейное свойство
Если функции f(P) и φ(Р) интегрируемы в области D, а а и β — любые вещественные числа, то функция af(P) + βφ(Р) также интегрируема в области D, причем
(1)
Интегрирование неравенств
Если функции f(P) и φ(Р) интегрируемы в области D и всюду в этой области
т. е. неравенства можно интегрировать. В частности, интегрируя очевидные неравенства
Площадь плоской области
Площадь плоской области D равна двойному интегралу по этой области от функции, тождественно равной единице. Действительно, интегральная сумма для функции f(P) = 1 в области D имеет вид
и при любом разбиении области D на частичные области Dk равна ее площади S. Но тогда и предел этой суммы, т. е. двойной интеграл, равен площади S области D:
(3)
Оценка интеграла
Пусть функция f(Р) непрерывна в ограниченной замкнутой области D, пусть М и т — наибольшее и наименьшее значения f(Р) в области D и S — ее площадь. Тогда
(4)
Аддитивность
Если функция f(P) интегрируема в области D и область D разбита на две области D1 и D2 без общих внутренних точек, то f<Р) интегрируема на каждой из областей D1 и D2, причем
Теорема о среднем значении
Теорема:
Если функция f(P) непрерывна в замкнутой ограниченной области D, то найдется по крайней мере одна тонка Ре области D такая, что будет справедлива формула
(6)
где S — площадь области D.
В самом деле, так как f(P) непрерывна в замкнутой ограниченной области D, то она принимает в D свое наибольшее значение М и свое наименьшее значение т. По свойству 4 об оценке интеграла имеем
Таким образом, число
заключено между наибольшим и наименьшим значениями функции f(P) в области D. В силу непрерывности функции f(P) в области D она принимает в некоторой точке Рe ∈ D значение, равное этому числу,
Значение f (Pe), определяемое по формуле (7), называется средним значением функции f(Р) в области D.
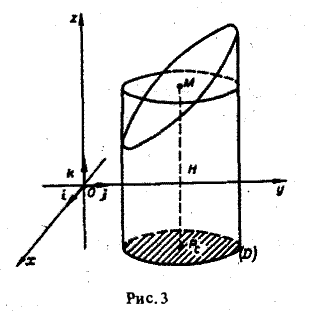
Геометрический смысл теоремы о среднем значении
Если в области D функция f(Р) ≥ 0, то формула (6) означает, что существует прямой цилиндр с основанием D (площадь которого равна S) и высотой H = f(Pe), объем которого равен объему цилиндрического тела (рис. 3).
Сведение двойного интеграла к повторному
Одним из эффективных способов вычисления двойного интеграла является сведение его к повторному.
Случай прямоугольника
Пусть область D — замкнутый прямоугольник П со сторонами, параллельными осям координат
Пусть функция f(x, у) непрерывна в прямоугольнике П. Двойной интеграл
можно интерпретировать как (алгебраический) объем цилиндрического тела с основанием П, ограниченного поверхностью
z = f(х, y).
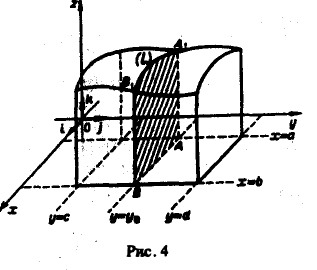
Рассмотрим соответствующее цилиндрическое тело. Проведем плоскость
перпендикулярную оси Оу (рис. 4). Эта плоскость рассечет цилиндрическое тело по криволинейной трапеции АВВ1А1, ограниченной сверху плоской линией z, описываемой уравнениями
Площадь трапеции АВВ1А1 выражается интегралом
где интегрирование производится по х, а уо — второй аргумент подынтегральной функции — рассматривается при этом как постоянный (с ≤ уо ≤ d). Величина интеграла (1) зависит от выбора значения уо. Положим
(2)
Выражение (2) дает площадь поперечного сечения цилиндрического тела как функции от у. Поэтому объем цилиндрического тела можно вычислить по формуле
С другой стороны, этот объем выражается двойным интегралом от функции f(х, у) по прямоугольнику П. Значит,
Заменяя S(y) его выражением (2), получим
Последнее соотношение обычно записывается так
(3)
Объем цилиндрического тела можно отыскать также по площадям сечений плоскостями х = х0. Это приводит к формуле
(4)
Каждое из выражений, стоящих в правых частях формул (3) и (4), содержит две последовательные операции обыкновенного интегрирования функции f(x, у). Они называются повторными интегралами от функции f(х, у) по области П.
Если f(x, у) непрерывна в замкнутом прямоугольнике П, то переход к повторным интегралам всегда возможен и
(5)
т. е. значения повторных интегралов от непрерывной функции f(х, у) не зависят от порядка интегрирования.
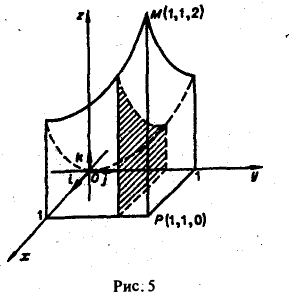
Пример:
Найти двойной интеграл от функции
4 Имеем (см. рис. 5):
Случай произвольной области
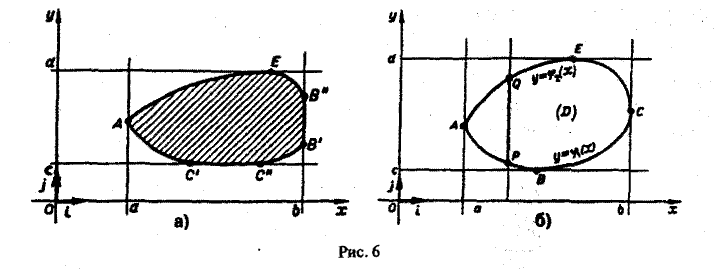
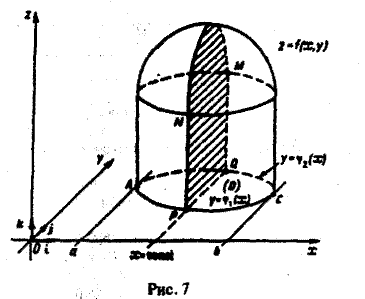
Предположим теперь, что областью интегрирования является произвольная ограниченная квадрируемая замкнутая область D на плоскости хОу, удовлетворяющая следующему условию: любая прямая, параллельная оси Оу, пересекает границу области D не более чем в двух точках или по целому отрезку (рис. 6 а). Заключим область D внутрь прямоугольника
так, как показано на рис. 66. Отрезок [а, b] является ортогональной проекцией области D на ось Ох, а отрезок [с, d] — ортогональной проекцией области D на ось Оу. Точками А и С граница области D разбивается на две кривые ABC и АЕС. Каждая из этих кривых пересекается с произвольной прямой, параллельной оси Оу, не более чем в одной точке. Поэтому их уравнения можно записать в форме, разрешенной относительно у:
Пусть f(x, у) — некоторая функция, непрерывная в области D. Рассечем рассматриваемое цилиндрическое тело плоскостью
х = const (а
В сечении получим криволинейную трапецию PQMN (рис.7), площадь которой выражается обыкновенным интегралом от функции f(x, у),рассматриваемой как функция одной переменной у. При этом переменная у изменяется от ординаты φ1(x) точки Р до ординаты φ2(х) точки Q; точка Р есть точка «входа» прямой х = const (в плоскости хОу) в область D, a Q — точка ее «выхода» из этой области. Так как уравнение кривой ABC есть у = φ(x), а кривой АЕС — у = φ2(х), то эти ординаты при взятом х соответственно равны φ1(x) и φ2(х). Следовательно, интеграл
дает нам выражение для площади плоского сечения цилиндрического тела как функции положения секущей плоскости x = const.
Объем всего тела будет равен интегралу от этого выражения по х в промежутке изменения х (a ≤ х ≤ b). Таким образом,
(8)
В частности, для площади S области D получим (9)
Предположим теперь, что каждая прямая
у = const (с ≤ у ≤ d)
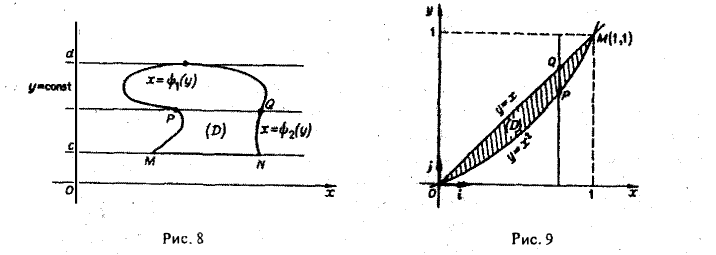
пересекает границу области D не более чем в двух точках Р и Q, абсциссы которых равны ψ1(у) и ψ2 <y) соответственно (или по целому отрезку) (рис. 8). Проводя аналогичные рассуждения, приходим к формуле
(10)
также сводящей вычисление двойного интеграла к повторному.
Пример:
Вычислить двойной интеграл от функции
f(x, у) = 2х — у + 3
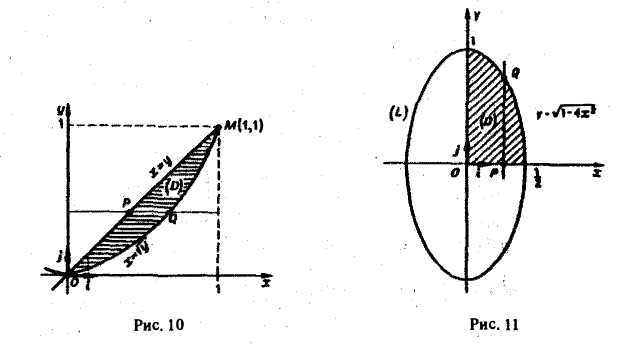
по области D, ограниченной линиями у = х и у = х2 (рис.9).
Первый способ. Изобразим область интегрирования D. Прямая у = х и парабола у = х2 пересекаются в точках O(0,0) и M(l,1). Значит, х изменяется в пределах от 0 до I, a ψ1(x) = х2 и ψ2(х) = х. Любая прямая х = const (0 ≤ х ≤ 1) пересекает границу области не более чем в двух точках. Поэтому применима формула (8):
Второй способ (рис. 10). Применяя формулу (10), получим тот же результат:
Пример:
Вычислить обьем тела, ограниченного поверхностью
и плоскостью хОу.
пересекается с плоскостью хОу по линии
Это — эллипс с полуосями а = 1/2 и b = 1 (рис. 11).
В силу симметрии данного тела относительно координатных плоскостей xОz и уOz получаем:
Замечание:
Если область D такова, что некоторые прямые (вертикальные или горизонтальные) пересекают ее границу более чем в двух точках, то для вычисления двойного интеграла по области D следует разбить ее подходящим образом на части, свести к повторному каждый из интегралов по этим частям и полученные результаты сложить.
Пример:
Вычислить двойной интеграл
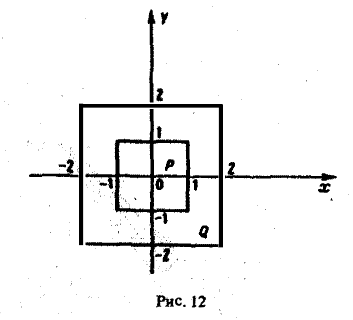
по области D, заключенной между двумя квадратами с центрами в начале координат и сторонами, параллельными осям координат, если сторона внутреннего квадрата равна 2, а внешнего — 4.
Функция
непрерывна как в большом квадрате Q, сторона которого равна 4, так и в малом квадрате Р, сторона которого равна 2 (рис. 12).
Согласно теореме 1, интегралы от функции е z+y по указанным квадратам существуют, так что величина искомого интеграла
Замена переменных в двойном интеграле
Понятие криволинейных координат точки:
Пусть в области D* плоскости uOv задана пара функций
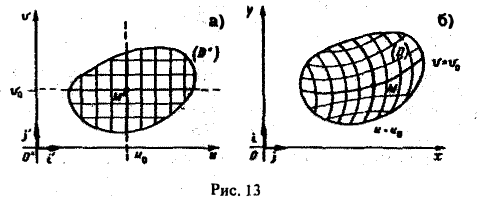
которые мы будем считать непрерывными в этой области и имеющими непрерывные частные производные. В силу уравнения (1) каждой точке М*(и, v) области D* отвечает одна определенная точка М(х, у) в плоскости хОу и тем самым точкам области D* отвечает некоторое множество D точек (x, у) в плоскости хОу (рис. 13). При этом говорят, что функции (1) осуществляют отображение области D на множество D.
Предположим, что различным точкам (и, v) отвечают различные точки (х,у). Это равносильно однозначной разрешимости уравнений (1) относительно и, v:
В этом случае отображение называется взаимно однозначным отображением области D* на область D. При таком преобразовании любая непрерывная кривая L*, лежащая в области D*, перейдет в непрерывную кривую L, лежащую в области D. Если функции g(х, у) и h(x,y) также непрерывны, то любая непрерывная линия L ⊂ D с помощью преобразования (2) перейдете непрерывную линию L* ⊂ D*.
По заданной паре uо, vo значений переменных и, v из области D* можно однозначно определить не только положение точки М*(и0, vo) в самой области D*, ной положение соответствующей точки М(хо, уо) в области D, xо = φ(uo, vo), уо = ψ(uо. vо). Это дает основание рассматривать числа u, v как некоторые новые координаты точки D области М на плоскости хОу. Их называют криволинейными координатами точки М.
Множество точек области D, у которых одна из координат сохраняет постоянное значение, называют координатной линией. Полагая в формуле (1) и = vo, получим параметрические уравнения координатной линии,
Здесь роль параметра играет переменная и. Придавая координате v различные (возможные для нее) постоянные значения, получим семейство координатных линий (v = const) на плоскости хОу. Аналогично получаем и другое семейство координатных линий (u = const).
При наличии взаимно однозначного соответствия между областями D* и D различные координатные линии одного и того же семейства Hie пересекаются между собой, и через любую точку области D проходит по одной линии из каждого семейства. Сетка криволинейных координатных линий на плоскости хОу является образом прямоугольной сетки на плоскости uOv (см. рис. 13).
Элемент площади в криволинейных координатах. Якобиан и его геометрический смысл
Выделим в области D* на плоскости Uo*V малый прямоугольник P’pj Р3Р4 со сторонами, параллельными осям координат О*и и О* v и длинами сторон ∆u и ∆v (для определенности считаем, что ∆u > О, ∆v > 0) соответственно (рис. 14а). Его площадь
Прямоугольник P*1P*2P*3P*4 переходит в криволинейный четырехугольник Р1Р2Р3Р4 в области D (рис. 146). Если вершины Р*i(i = 1, 2, 3,4) имеют координаты
то, согласно формулам (1), соответствующие им вершины Рi имеют координаты
Пользуясь формулой Тейлора для функции двух переменных и ограничиваясь членами первого порядка относительно ∆и и ∆v, получим следующие приближенные значения координат для вершин четырехугольника Р1Р2Р3Р4:
где функции φ, ψ и все их производные вычислены в точке (и, v). Найденные выражения для координат точек показывают, что с точностью до малых высшего порядка четырехугольник Р1Р2Р3Р4 есть параллелограмм. Это следует из того, что
Тогда площадь ∆S четырехугольника Р1Р2Р3Р4 можно приближенно выразить через длину векторного произведения 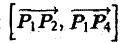
называется функциональным определителем функций φ<и, v), ψ (u, v), или якобианом. Итак, (6)
Выражение в правой части (6) называется элементом площади в криволинейных координатах. Так как ∆и ⋅ ∆v,to из формулы (6) получаем, что
Равенство (7) является приближенным. Однако в пределе, когда диаметры площадок ∆S* и ∆S стремятся к нулю, оно переходит в точное:
Из формул (7) и (8) видано, что абсолютная величина якобиана играет роль локального коэффициента растяжения области D* (в данной точке (u, v)) при отображении ее на область D при помощи формул преобразования (1).
Формула замены переменных в двойном интеграле
осуществляют взаимнооднозначное отображение области D* на D и имеют непрерывные частные производные первого порядка. Пусть в области D на плоскости хОу задана непрерывная функция
Каждому значению функции z = f(x, у) в области D соответствует равное значение функции z = F(u, v) в области D*, где
Разобьем область D* на частичные области и построим соответствующее разбиение области D. Выберем в соответствующих частичных областях точки (u, v) и (х, у) так, чтобы значения функций F(u, v) и f(x, у) в них совпадали, и составим интегральные суммы для функций z = f(x, у) и F(u,v) по областям D и D*. Получим
и J(и, v) — якобиан функций φ(и, v) и ψ =(u, v). Переходя в равенстве (9) к пределу при стремлении к нулю наибольшего диаметра d* частичных областей D*k (в силу непрерывности отображения (1) будет стремиться к нулю и наибольший из диаметров d частичных областей в D), будем иметь
Условие J ≠ 0 является условием локальной взаимноoднозначности отображения, осуществляемого функциями φ(и, v) и ψ =(u, v).
Теорема:
Для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции f(x, у) переменные х и у соответственно через φ(и, v) и ψ =(u, v), а элемент площади dx dy — его выражением в криволинейных координатах:
Пример:
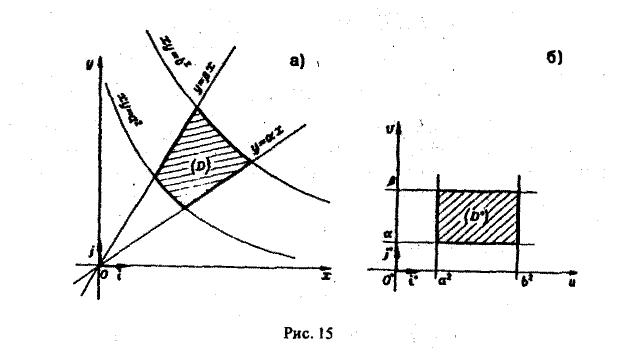
Найти площадь фигуры, ограниченной гиперболами
где х > 0, у > 0, 0
где 0
по области D. Введем новые, криволинейные координаты и и v формулами
Из условия задачи ясно, что a2 ≤ u ≤ b2. а ≤ v ≤ β. Значит, в плоскости uOv мы получили прямоугольник (рис. 15b)
— фигуру Солее простую, чем заданная фигура D.
Выразим х и у из соотношений (11) через u и v:
По формуле (10) при f(x,y) = 1 получим
Двойной интеграл в полярных координатах
Вычисление двойного интеграла часто упрощается заменой прямоугольных координат х и у полярными координатами р и φ по формулам
Элемент площади в полярных координатах имеет вид
(13)
и формулу перехода от интеграла в декартовых координатах к интегралу в полярных координатах можно записать так:
(14)
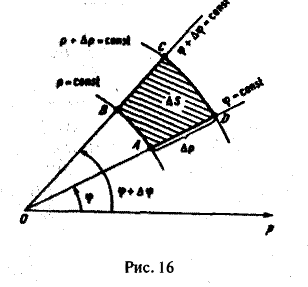
Элемент площади в полярных координатах можно подучить и из геометрических соображений (см. рис. 16).
Площадь заштрихованной на рисунке области
Отбрасывая бесконечно малую величину высшего порядка, получаем
за элемент площади в полярных координатах.
Итак, чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно х к у в подынтегральной функции заменить соответственно через р cos φ и р sin φ, а элемент площади в декартовых координатах dx dy заменить элементом площади в полярных координатах р dp dφ.
Займемся теперь вычислением двойного интеграла в полярных координатах. Как и в случае прямоугольных декартовых координат, вычисление интеграла в полярных координатах осуществляется путем сведения его к повторному интегралу.
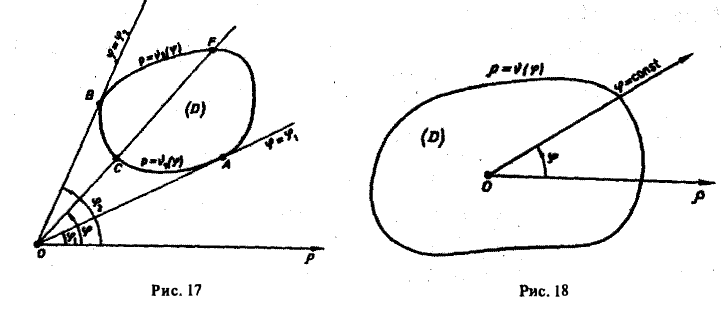
Рассмотрим сначала случай, когда полюс О лежит вне заданной области D. Пусть область D обладает тем свойством, что любой луч, исходящий из полюса (координатная линия φ = const) пересекает ее границу не более чем в двух точках или по целому отрезку (рис. 17). Отметим крайние значения φ1 и φ2 полярного угла φ, φ1 ≤ φ ≤ φ2-Числа φ1 и φ2 являются пределами внешнего интегрирования.
Луч φ = φ1 проходит через точку А контура области D, а луч φ = φ2 — через точку В. Точки А и В разбивают контур области D на две части: АС В и AFB. Пусть р = v1( φ ) и р = v2( φ ) — их полярные уравнения, причем v1( φ ) и v2( φ ) — однозначные непрерывные функции φ, удовлетворяющие условию
Функции v1( φ ) и v2( φ ) являются пределами внутреннего интегрирования. Переходя к повторным интегралам, получаем следующую формулу
(15)
В частности, для площади S области D при F(p, φ) = 1 получаем
Пусть теперь полюс О расположен внутри области D. Предположим, что область D является звездной относительно полюса, т. е. любой луч φ = const пересекает границу области только в одной точке или по целoму отрезку (рис. 18). Пусть р = v( φ ) — уравнение границы области в полярных координатах. Тогда
(16)
Пример:
— четверть единичного круга, расположенная в первом квадранте.
Перейдем к полярным координатам
= р cos φ, у = р sin φ.
Тогда областью интегрирования будет прямоугольник
Преобразованный интеграл I легко вычисляется:
Замечание:
Если якобиан отличен от нуля в области D, то отображение в некоторой окрестности каждой точки этой области является взаимнооднозначным. При этом может, однако, случиться, что отображение всей области не будет взаимнооднозначным. Рассмотрим отображение, определяемое функциями
Якобиан этих функций равен
и, следовательно, везде отличен от нуля. Несмотря на это, для u = 0, v = 0 и дня и = 0, v = 2π мы получим х = 1, у = 0, так что это отображение не является взаимнооднозначным.
С другой стороны, если якобиан отображения обращается в нуль в какой-нибудь точке, то, тем не менее, отображение в окрестности этой точки может оказаться взаимно однозначным. Например, для отображения, определяемого функциями
равен нулю и при и = 0, и при v = 0, но отображение является взаимнооднозначным. Обратное отображение определяется функциями
Площадь поверхности
Интеграл по площади поверхности. Вычисление площади поверхности
Пусть задана поверхность π, однозначно проектирующаяся на область D плоскости хОу. Это означает, что данная поверхность задается уравнением
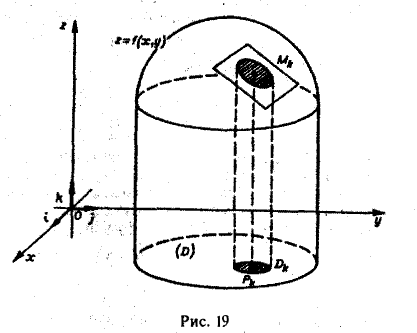
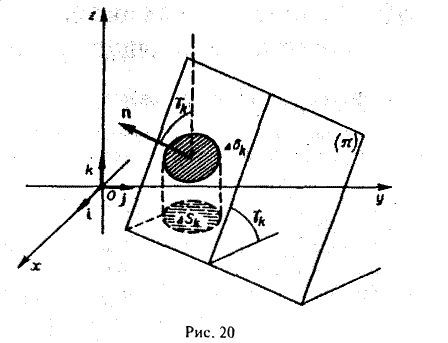
Будем считать поверхность гладкой; это означает, что в области D функция f(x, у) непрерывна и имеет непрерывные частные производные f’x(x, у) и f’y(x, у). Разобьем область D на квадрируемые подобласти
без общих внутренних точек, площади которых обозначим соответственно через
Пусть d — наибольший из диаметров частичных областей Dk (k = 1,2,…, п). В каждой подобласти Dk выберем произвольную точку Pk( ξk, ηk)- На поверхности π точке Рk будет соответствовать точка Mk( ξk, ηk, ζk), где ζk= f( ξk, ηk) (рис. 19). Проведем в точке Мk касательную плоскость к поверхности π. Ее уравнение имеет следующий вид __(1)
Построим на границе частичной области dk, как на направляющей, цилиндрическую поверхность с образующими, параллельными оси Oz. Эта цилиндрическая поверхность вырежет из касательной плоскости, проведенной через точку Мk, область πk площади ∆qк. Площадка Пk проектируется на элементарную область Dk плоскости хОу взаимнооднозначно.
Определение:
Если при d→0 сумма (2) имеет конечный предел S,
то число S называется площадью поверхности π.
Таким образом, мы заменяем данную поверхность «чешуйчатой», затем подсчитываем плошадь этой «чешуйчатой» поверхности и переходим к пределу при стремлении диаметра «чешуек» к нулю (диаметры чешуек стремятся к нулю при d —> 0).
Перейдем теперь к выводу формулы, по которой вычисляют площадь поверхности. Известно, что площадь проекции плоской фигуры на какую-нибудь плоскость равна произведению площади проектируемой фигуры на косинус острого угла между плоскостью проекции и плоскостью, в которой лежит проектируемая фигура.
Обозначим через γk угол между касательной плоскостью к поверхности π в точке Мk и плоскостью хОу (рис. 20). Тогда
Но угол γk есть в то же время угол между осью Oz и нормалью касательной плоскости к поверхности (1). Обозначим вектор нормали к касательной плоскости к поверхности в точке Мk через
а через п2 = — единичный вектор оси Оz. Тогда получим
По условию функции f’z(x,y) и f’у(х, у) непрерывны в области D. Следовательно, функция
непрерывна, а, значит, и интегрируема в области D. Поэтому при d → 0 сумма (5) имеет конечный предел,
Учитывая равенство (3), определяющее площадь S поверхности заключаем, что
(6)
где Dxy — проекция поверхности я- на плоскость хОу. Выражение
(7)
называется элементом площади поверхности.
Если спроектировать участок поверхности π на плоскость хОу, то получим
(8)
где Dyz — проекция участка поверхности на плоскость хОу. Соответственно, при проектировании на плоскость yOz имеем
(9)
где Dyz — проекция участка поверхности на плоскость yOz.
Пример:
Найти площадь сферы радиуса R с центром в начале координат
Уравнение верхней полусферы —
Искомая площадь S
Отметим следующие полезные формулы:
1) для элемента площади цилиндрической поверхности радиуса R
(10)
2) для элемента площади сферической поверхности радиуса R
(11)
Используя формулу (11) для элемента площади сферической поверхности получим площадь сферы:
Интеграл по площади поверхности (интеграл по поверхности 1-го рода)
Пусть на гладкой поверхности π задана непрерывная функция f(М). Разобьем поверхность π на части
соответственно, выделим на каждой из частичных поверхностей по произвольной точке Mi, Мг,… , Мп и составим сумму
которую будем называть интегральной суммой для функции f<М) по площади поверхности π.
Определение:
Если при стремлении к нулю наибольшего из диаметров частичных поверхностей πk интегральная сумма (12) имеет конечный предел, не зависящий ни от способа разбиения поверхности т на части, ни от выбора точек Mk, то этот предел называется интегралом от функции f(M) по площади поверхности π (интегралом по поверхности 1-го рода) и обозначается символом
где dσ — элемент площади поверхности.
Общие свойства двойных интегралов легко переносятся на интегралы по площади поверхности. В частности, если поверхность π разбита на неперекрывающиеся части π1, π2,…, πn, то
Теорема:
Пусть -к — гладкая поверхность, заданная уравнением z = φ(x, у), где (х,у) ∈ D, причем функция φ(х, у) имеет непрерывные частные производные в некоторой области D1, D ⊂ D1. Пусть, далее, f(x, у, z) — непрерывная функция, определенная на поверхности π. Тогда справедливо равенство
где μ(Р) ≥ 0 на π, можно истолковать как массу π оболочки, представляющей собой поверхностью, на которой масса распределена с поверхностной плотностью μ = μ(Р).
Пример:
Найти массу параболической оболочки
плотность которой меняется по закону μ = z (рис. 21).
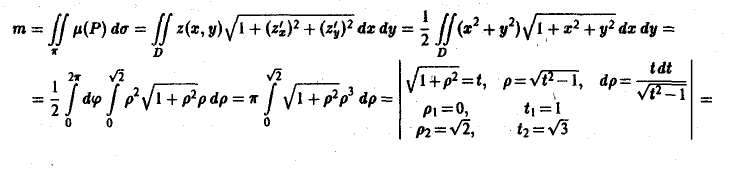
Тройной интеграл
Задача, приводящая к тройному интегралу
Пусть дано материальное тело, представляющее собой пространственную область Ω, заполненную массой. Требуется найти массу то этого тела при условии, что в каждой точке Р ∈ Ω известна плотность
Разобьем область Ω на неперекрывающиеся кубируемые (т. е. имеющие объем) части
соответственно. В каждой из частичных областей Ωk выберем произвольную точку Рk. Примем приближенно, что в пределах частичной области Ωk плотность постоянна и равна μ(Рk)- Тогда масса ∆тk этой части тела выразится приближенным равенством
а масса всего тела будет приближенно равна
Пусть d — наибольший из диаметров частичных областей Ωk(k = 1,2,…, п). Если при d —> О сумма (1) имеет конечный предел, не зависящий ни от способа разбиения области Ω на частичные подобласти, ни от выбора точек Рk ∈ Ωk, то этот предел принимается за массу т заданного тела,
Пусть в замкнутой кубируемой области Ω определена ограниченная функция
f(Р), Р ∈ Ω.
Разобьем Ω на п непересекающихся кубируемых частей
а их объемы обозначим через
соответственно. В каждой частичной подобласти Ωk произвольным образом выбираем точку Рk(хk, yk, zk) и составляем интегральную сумму
Пусть d — наибольший из диаметров частичных областей Ωk(k = 1, 2,…, п).
Определение:
Если при d → 0 интегральные суммы а имеют предел, не зависящий ни от способа разбиения области Ω на частичные подобласти Ωk, ни от выбора точек Рk ∈ Ωk, то этот предел называется тройным интегралом от функции f(x, у, z) по области Ω и обозначается символом
При этом функция f(х, у, z) называется интегрируемой в области Ω.
Таким образом, по определению имеем
Возвращаясь к задаче о вычислении массы тела, замечаем, что предел (2) есть тройной интеграл от функции μ(Р) по области Ω. Значит,
Здесь dx dy dz — элемент объема dv в прямоугольных координатах.
Теорема 6. Если функция f(x, у, z) непрерывна в замкнутой кубируемой области Ω, то она интегрируема в этой области.
Свойства тройных интегралов
Свойства тройных интегралов аналогичны свойствам двойных интегралов. Перечислим основные из них.
Пусть функции f(Р) и φ(Р) интегрируемы в кубируемой области Ω.
1, Линейность.
где а и β — произвольные вещественные постоянные.
2. f(Р) ≤ φ(P) всюду в области Ω, то
3. Если f(P) ≡ 1 в области Ω, то
где V — объем области Ω.
4. Если функция f(P) непрерывна в замкнутой кубируемой области Ω и М и т — ее наибольшее и наименьшее значения в Ω, то
где V — объем области Ω.
5. Аддиктивность. Если область Ω разбита на кубируемые области Ω1 и Ω2 без общих внутренних точек и f(Р) интегрируема в области Ω,то f(P) интегрируема на каждой из областей Ω1 и Ω2, причем
Теорема о среднем значении
Теоремa:
Если функция f(P) непрерывна в замкнутой кубируемой области Ω, то найдется точка Рс ∈ Ω , такая, что будет справедлива формула
где V — объем области Ω (напомним, что область — связное множество).
Вычисление тройного интеграла в декартовых координатах
Как и при вычислении двойных интегралов, дело сводится к вычислению повторных интегралов. Предположим, что функция f(х, у, z) непрерывна в некоторой области Ω.
1-й случай. Область Ω представляет собой прямоугольный параллелепипед
проектирующийся на плоскость yOz в прямоугольник R;
Заменяя двойной интеграл через повторный, окончательно получим
(2)
Таким образом, в случае, когда область Ω — прямоугольный параллелепипед, мы свели вычисление тройного интеграла к последовательному вычислению трех обыкновенных интегралов.
Формулу (2) можно переписать в виде
есть ортогональная проекция параллелепипеда Ω на плоскость хОу.
2-й случай. Рассмотрим теперь область Ω такую, что ограничивающая ее поверхность S пересекается любой прямой, параллельной оси Oz, не более чем в двух точках или по целому отрезку (рис.22).
Пусть z = φ1(x,y) уравнение поверхности S1, ограничивающей область Ω снизу, а поверхность S2, ограничивающая область Ω сверху, имеет уравнение z = φ2(x,y).
Пусть обе поверхности S1 и S2 проектируются на одну и ту же область плоскости хОу. Обозначим ее через D, а ограничивающую ее кривую через L. Остальная часть границы S тела Ω лежит на цилиндрической поверхности с образующими, параллельными оси Oz, и с кривой L в роли направляющей. Тогда по аналогии с формулой (3) получим
Если область D плоскости хОу представляет собой криволинейную трапецию, ограниченную двумя кривыми у = ψ1(х) И y = ψ2(х) (а ≤ х ≤ b), то двойной интеграл в формуле (4) можно свести к повторному, и мы получим окончательно
(4)
Эта формула является обобщением формулы (2).
Пример:
Вычислить объем тетраэдра, ограниченного плоскостями
x = 0, у = 0, z = 0 и х + 2у + z- 6 = 0.
Проекцией тетраэдра на плоскость хОу служит треугольник, образованный прямыми
x = 0, у = 0 и х + 2у = 6,
так что х изменяется от 0 до 6, а при фиксированном х (0 ≤ х ≤ 6) у изменяется от 0 до 3 — π/2 (рис. 23). Если же фиксированы и х, и у, то точка может перемещаться по вертикали от плоскости z=0 до плоскости x + 2y + z- 6 = 0, т. е. г меняется в пределах от 0 до 6 — х — 2у. По формуле (5) при f<x, у, z) = 1 получаем
Вычисление тройного интеграла в цилиндрических и сферических координатах
Вопрос о замене переменных в тройном интеграле решается таким же путем, как и в случае двойного интеграла. Пусть функция f(x,y, z) непрерывна в замкнутой кубируемой области Ω, а функции
непрерывны вместе со своими частными производными первого порядка в замкнутой кубируемой области Ω*. Предположим, что функции (1) устанавливают взаимнооднозначное соответствие между всеми точками ( ξ, η, ζ) области Ω*, с одной стороны, и всеми точками (х, у, z) области Ω — с другой. Тогда справедлива формула замены переменных в тройном интеграле —
(2)
— якобиан системы функций (1).
На практике при вычислении тройных интеграловчасто пользуются заменой прямоугольных координат цилиндрическими и сферическими координатами.
Тройной интеграл в цилиндрических координатах
В цилиндрической системе координат положение точки Р в пространстве определяется тремя числами р, φ, z, где р и φ — полярные координаты проекции Р» точки Р на плоскость хОу, a z — аппликата точки Р (рис. 24). Числа р, φ, z называются цилиндрическими координатами точки Р.
В системе цилиндрических координат координатные поверхности
р = const, φ = const, z = const
соответственно описывают: круговой цилиндр, ось которого совпадает с осью Oz, полуплоскость, примыкающую к оси Oz, и плоскость, параллельную плоскости хОу.
Цилиндрические координаты связаны с декартовыми следующими формулами
x = p cost φ, y = p sin φ, Z = Z (3)
(см. рис. 24). Для системы (3), отображающей область Ω на область Ω*, имеем
Так как p ≥ 0, то
|J|= p
и формула (2) перехода от тройного интеграла в прямоугольных координатах к интегралу в цилиндрических координатах принимает вид
(4)
называется элементом объема в цилиндрических координатах.
Это выражение для элемента объема может быть получено и из геометрических соображений. Разобьем область Ω на элементарные подобласти координатными поверхностями
р = const, φ = const, z = const
и вычислим объемы полученных криволинейных призм (рис. 25).
Отбрасывая бесконечно малую величину более высокого порядка, получаем
Это позволяет принять за элемент объема в цилиндрических координатах следующую величину
dv = p dp dφ dz.
Пример:
Найти объем тела, ограниченного поверхностями
В цилиндрических координатах заданные поверхности будут иметь уравнения
(см. формулы (3)). Эти поверхности пересекаются по линии г, которая описывается системой уравнений
а ее проекция на плоскость хОу системой
р = 1, z = 0.
Искомый объем вычисляется по формуле (4), в которой f ≡ 1.
Тройной интеграл в сферических координатах
В сферической системе координат положение точки Р(х, у, z) в пространстве определяется тремя числами r, φ, θ, где r — расстояние от начала координат до точки Р, φ — угол между осью Ох и проекцией радиуса-вектора ОР точки Р на плоскость хОу, а θ — угол между осью Oz и радиусом-вектором ОР точки Р, отсчитываемый от оси Oz (рис. 27).
Ясно, что 0 ≤ r
Вычислим якобиан функций (5). Имеем
и формула (2) принимает вид
(6)
Элемент объема в сферических координатах —
Выражение для элемента объема можно получить и из геометрических соображений. Рассмотрим элементарную область в пространстве, ограниченную сферами радиусов г и г + dr, конусами в и в + d$ и полуплоскостями
Пример:
Найти объем выпуклого тела П, вырезаемого из конуса
Переходим к сферической системе координат
Из первых двух уравнений видно, что а ^ г ^ 6. Из третьего уравнения находим пределы изменения угла в:
Тем самым, 0 ≤ θ ≤ π/4. Полагая в формуле (6) f(x, у, z) ≡ 1, получим
Приложения двойных и тройных интегралов
Масса плоской фигуры
Пусть задана плоская ограниченная фигура D, по которой непрерывным образом распределена масса с поверхностной плотностью μ(Р) = μ(х, у) ≥ 0, где μ(х, у) — функция, непрерывная в D. Разобьем фигуру D на п частей
без общих внутренних точек, площади которых соответственно равны
В каждой части (к = 1,2,…, п) произвольно выберем точку Рk(хk, уk) и вычислим в ней плотность μ(xk, yk). В силу непрерывности μ(х, у) можно считать, что масса mk части Dk фигуры D приближенно равна μ(хk, yk) ∆Sk, a масса всей фигуры — сумме
Последняя является интегральной суммой для непрерывной функции μ(x, у) в области D. Переходя к пределу при d → 0 (здесь d — наибольший из диаметров частичных областей Dk(k = 1,…, п)), получим точное равенство
(1)
Если масса распределена равномерно по всей фигуре, μ = const, то формула (1) принимает вид
где S — площадь фигуры D.
Пример:
Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов r и R, где r
Значит, масса кольца
Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести
Статическим моментом Мх материальной точки массы m относительно оси Ох называется произведение ту, где у — ордината материальной точки, т. е.
Здесь у может быть как положительным, так и отрицательным числом.
Разбивая фигуру D на части D1,…, Dn, выбирая в каждой части Dk произвольно точку Pk(xk, yk) и считая, что масса этой k-й части приближенно равна μ(хk, yk) ∆Sk и сосредоточена в точке Pk(xk,yk), запишем приближенно величину статического момента фигуры D относительно оси Ох. Имеем
где ∆Sk — площадь части Dk, а μ(х, у) — поверхностная плотность. Переходя к пределу при d —» 0, получаем
(3)
Статический момент фигуры D относительно оси Оу находится по аналогичной формуле
(4)
Если известны статические моменты Мх и Му и масса m плоской фигуры, то координаты центра тяжести этой фигуры находятся по следующим формулам
(5)
Если μ = const, т = μS, где S — площадь фигуры D, и формулы (5) принимают вид:
(6)
Пример:
Hайти центр тяжести однородной плоской фигуры, ограниченной косинусоидой
осью Ох и осью Оу.
Так как фигура — однородная, то координаты центра тяжести будем искать по формулам (б). Найдем сначала площадь 5 заданной фигуры. Имеем
Затем найдем статические моменты Mz и Му
Теперь no формулам (6) получаем
Моменты инерции плоской фигуры относительно осей координат
Рассуждая аналогично изложенному выше, легко установить, что элементарные моменты инерции относительно осей Ох и Оу будут соответстве нно равны
Интегрируя по плоской фигуре D, получим формулы для самих моментов инерции (7), (8)
где, как и ранее, μ(x, у) — поверхностная плотность распределения масс.
Вычисление массы тела
Рассматривая задачу, приводящую к тройному интегралу, мы показали, что если известна плотность распределения масс ц(х, у, z) в каждой точке некоторого тела Ω, то масса этого тела вычисляется по формуле
(9)
Мы предполагаем, что функция μ(х, у, z) непрерывна в области Ω.
Пример:
Вычислить массу m тела, ограниченного полусферами
и плоскостью хОу, если плотность в каждой точке пропорциональна расстоянию от этой точм до начала координат.
По условию задачи плотность μ в точке (x,y,z) выражается формулой
где к > 0 — коэффициент пропорциональности. Тогда
Переходя к сферическим координатам, получим, что
Статические моменты тела относительно координатных плоскостей. Центр тяжести
Напомним, что задача о вычислении статических моментов и центра тяжести плоской фигуры решалась при помощи двойных интегралов (см. формулы (3), (4) и (5)). Задачи о вычислении статических моментов тела Ω относительно координатных плоскостей и отыскания центра тяжести тела Ω решаются аналогичным способом при помощи тройных интегралов. Например, элементарный статический момент относительно плоскости хОу равен
где μ(x, у, z) — плотность. Отсюда статический момент
(10)
Аналогично выписываются статические моменты относительно плоскостей хОу и Y
Вычислив массу m тела Ω и его статические моменты, легко найти координаты центра тяжести тела: (11)
Если тело однородно, то плотность μ = const и формулы (11) упрощаются — постоянный множитель μ в числителе можно вынести за знак интеграла и сократить на него числитель и знаменатель (ибо т = μy). Тогда получим (12)
где V — объем тела Ω.
Пример:
Найти координаты центра тяжести однородного полушара радиуса R.
Считаем, что центр шара находится в начале координат, а рассматриваемая фигура — полушар — расположена над плоскостью хОу. Тогда в силу симметрии имеем
Объем полушара равен
Найдем статический момент относительно плоскости хОу :
и 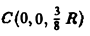
Понятие о несобственном кратном интеграле по неограниченной области
При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования
монотонно исчерпывающих область D, т. е.
Dn —> D при п —> ∞.
Например, если область интегрирования совпадает со всей плоскостью хОу, то за последовательность можно принять совокупность концентрических кругов
Определение:
Несобственным интегралом от функции f(х, у) по неограниченной области интегрирования D называется предел последовательности интегралов
не зависящий от выбора последовательности Db.
Итак, по определению
(2)
Если предел (1) существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае — расходящимся.
Пример:
где область интегрирования
В качестве областей интегрирования выберем круги
радиуса п (n = 1,2,… ). Переходя к полярным координатам, получим
Итак, интеграл (3) сходится и равен π.
Для интеграла по неограниченной области D справедлив следующий Признак сравнения. Если 0 ≤ f(x, у) ≤ g(х, у) ∀(x, у) ∈ D,u интеграл
сходится, то сходится и интеграл
Если же интеграл
расходится, то расходится и интеграл
Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования:
(4)
Пример:
то, согласно соотношению (4),
Переходя в двойном интеграле к полярным координатам, получим новую область интегрирования
Несобственные интегралы от функции трех, четырех и большего числа переменных по неограниченным областям определяются аналогично.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📺 Видео
Математика без ху!ни. Двойной интеграл, вычисление двумя способами.Скачать
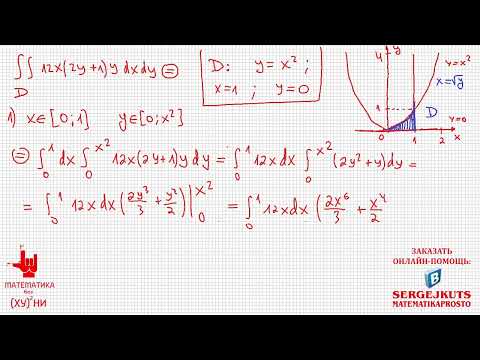
Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать