Что такое треугольник токов

Представим комплексную проводимость в алгебраической форме

Действительную часть комплексной проводимости С называют активной проводимостью, а мнимую В — реактивной. На рис. 2.10.2, а сделаны построения, соответствующие комплексному выражению (2.10.5).

Рис. 2.10.2. Треугольники проводимостей (а) и токов (б)

Заштрихованный прямоугольный треугольник на рис. 2.10.2, а называют треугольником проводимостей. Из треугольника очевидны соотношения

Выразим активную и реактивную составляющие проводимости ветви через ее активное и реактивное сопротивления. Рассмотрим, например, проводимость ветви с элементами /?, и]Хр

При получении соотношения (2.10.7) числитель и знаменатель умножены на сопряженный комплекс

Следует обратить внимание на то, что мнимая часть комплексной проводимости ветви с индуктивным элементом отрицательная. Если бы подобным образом было получено соотношение для второй ветви, содержащей емкостный элемент, то формулы имели бы тот же вид, но мнимая часть была бы положительной.

Итак,

Построение треугольника тока очевидно из рис. 2.10.2, б. На векторной диаграмме рис. 2.10.2, б вектор тока спроецирован на направление вектора напряжения. Полученный при этом треугольник называют треугольником тока. Катеты прямоугольного треугольника тока называют активной и реактивной составляющими: активная составляющая тока /_а параллельна напряжению, а реактивная /_р — ортогональна. Из треугольника тока можно получить следующие выражения активной и реактивной составляющих тока:

Поскольку I = иУ, соэср = С/У, эшср = В/У, получаем после подстановки в (2.10.9а)

Фазовые соотношения. Резонанс токов. Обратимся к векторной диаграмме цепи рис. 2.10.1, изображенной на рис. 2.10.3, а.

Рис. 2.103. Векторные диаграммы электрической цени с параллельным соединением двух ветвей при разных соотношениях сопротивлений ветвей

Построение диаграммы удобно начинать с вектора входного напряжения Ц, который является одним и тем же для обеих параллельных ветвей. Ток первой ветви /_1? содержащей индуктивный элемент, отстает по фазе от напряжения на угол ср, = , dvctg(Х^//?,). Ток второй ветви /₂, содержащей емкостный элемент, на угол ср._; = -аrctg(X_c/R.₎) опережает по фазе напряжение. Вектор тока неразветвленного участка / найден по первому закону Кирхгофа. Поэтому модули активной /_а и реактивной /_р составляющих тока неразветвленного участка цепи связаны с соответствующими составляющими токов ветвей соотношениями /_а= /_1а + /_2а и /_р = /_1р— /_2р. Активные составляющие токов /_1а, /_2а находятся в фазе, а реактивные /_1р, /_2р — в противофазе.

Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Введение

Экспериментально на основании показаний приборов определить активные и реактивные сопротивления приемников, установить влияние характера нагрузки на величины активной, реактивной и полной мощностей при параллельном соединении активного, индуктивного и емкостного приемников.

Методом векторных диаграмм установить влияние характера нагрузки на величину коэффициента мощности и угла сдвига фаз между током и напряжением.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Теоретическое введение

Видео:Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Треугольник токов. Треугольник проводимостей

Рис. 1 — Параллельное соединение элементов

Цепь, все ветви которой подключены к одной паре узлов, называется параллельной. Если напряжение на зажимах линейной цепи меняется по гармоническому закону , то по гармоническому закону будут меняться и токи в ветвях цепи. Тогда на основании первого закона Кирхгофа мгновенное значение тока i в неразветвленной части цепи в любой момент времени будет равно сумме мгновенных значений токов в ветвях цепи, т.е.

где — амплитудные значения токов в активной, индуктивной и емкостной ветвях цепи соответственно. Так как токи в ветвях цепи не совпадают по фазе, действующее значение тока в неразветвленной части цепи может быть получено векторным сложением:

На основании уравнений (2), (3) строится векторная диаграмма токов и напряжения. Построение векторной диаграммы начинается с вектора напряжения, на выбор начальной фазы которого не налагается каких-либо ограничений. В выбранном масштабе напряжения направим его горизонтально вправо. В выбранном масштабе тока строим соответствующие векторы тока из уравнения (3). Фазы векторов напряжений берутся в соответствии с уравнениями (2).

Синфазно с вектором напряжения откладывается вектор тока в активной ветви цепи . Вектор реактивного индуктивного тока строится сдвинутым относительно вектора напряжения в направлении движения часовой стрелки на угол — /2. Вектор реактивного емкостного тока строится сдвинутым относительно вектора напряжения против направления движения часовой стрелки на угол 2 (где: g, bL, bC — активная, индуктивная и емкостная проводимости, соответственно. Они легко вычисляются, если известны параметры ветвей , , где: r, x, z — активное, реактивное и полное сопротивление ветвей, соответственно. Проводимость выражается в Ом-1 или См (сименс)). Вектор тока , протекающего в неразветвленной части цепи, находится сложением векторов по правилам векторной алгебры (рис.2).

Рис. 2 — Векторная диаграмма токов

Действующее значение этого тока можно определить из заштрихованного треугольника, который называется треугольником токов.

Подставляя в уравнение (4) выражение для составляющих токов, получим:

где — полная проводимость цепи.

Выражение (6) является законом Ома для цепи с параллельным соединением элементов.

Из треугольника токов следует, что

Рис. 3 — Треугольник проводимостей

Поделив все стороны треугольника токов на напряжение, получим треугольник проводимостей рис. 3., который позволяет определить угол сдвига фаз между током и напряжением, если известны параметры элементов. Он определяется соотношением реактивных и активных проводимостей цепи:

Из треугольника проводимостей следует, что: Видео:Что такое Треугольник Карпмана?Скачать Треугольник токов, проводимостей Треугольник токов получим, если разложить ток разветвленной цепи на активную и реактивную составляющие. Активная составляющая совпадает по фазе с напряжением. Реактивная составляющая отстает по фазе от напряжения на угол 90°, если bL>bc (рис. 2.10, б), и опережает по фазе напряжение на угол 90°, если bL 2 +b 2 = yjg Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать Резонанс токов Явление резонанса в цепи переменного тока, содержащей параллельно соединенные индуктивный и емкостный элементы, называют резонансом токов. Условие возникновения резонанса токов — равенство нулю реактивной проводимости цепи b = bc —bL = 0 или =bc. Признаки резонанса токов: угол сдвига фаз между током в не-разветвленной части цепи и напряжением равен нулю, коэффициент мощности равен единице, индуктивная составляющая тока равна емкостной, полная проводимость равна активной. Видео:Мощность трехфазного напряжении при подключении нагрузки звездой и треугольникомСкачать Символический метод расчета цепей синусоидального тока Сущность символического метода состоит в переходе от интегро-дифференциальных уравнений, составленных для мгновенных значений синусоидальных величин, к алгебраическим уравнениям, составленным относительно комплексов (символов) тока, напряжения, ЭДС [3]. Мгновенное значение синусоидальной ЭДС е = Ет sin(co? + ) заменяют комплексной амплитудой Ет = Eme jyVe или комплексным действующим значением Е = Ее^ е . Аналогично для синусоидальных токов и напряжений: Z R + jX R 2 + X 2 R 2 + X 2 Закон Ома в комплексной форме для пассивного участка цепи для участка цепи, содержащего синусоидальную ЭДС, Законы Кирхгофа в комплексной форме. Первый закон Кирхгофа: сумма комплексов токов ветвей подключенных к узлу равна нулю Zb=o. Как и в цепях постоянного тока, при составлении уравнений со знаком «+» берутся токи, направленные к узлу, а со знаком «-» берутся токи, направленные от узла (или наоборот). Второй закон Кирхгофа: алгебраическая сумма комплексных падений напряжения в замкнутом контуре равна алгебраической сумме комплексных ЭДС, действующих в этом же контуре: Sz,z,=t^— При составлении уравнений падения напряжения берутся со знаком «+», если направление тока совпадает с направлением обхода контура, со знаком «-» — в противном случае. ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура, со знаком «-» — в противном случае. Комплексная мощность. Полная мощность в комплексной форме есть произведение комплексного напряжения на комплексно сопряженный ток: Активная мощность равна действительной части полной мощности, реактивная мощность равна мнимой части полной мощности. Баланс мощностей в комплексной форме имеет вид: 🎬 Видео Трехфазная система. Анимация электрических процессовСкачать Соединение обмоток треугольникомСкачать Сокрушительная битва | Электрические цепи-1. 9-11 классСкачать Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать Трехфазные электрические цепи │Теория ч. 1Скачать Векторная диаграммаСкачать Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать Векторная диаграмма при соединении приемника треугольникомСкачать 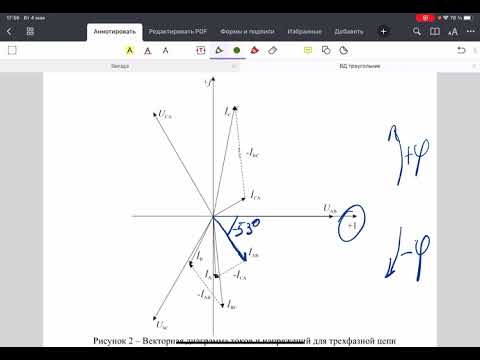Пуск электродвигателя, без пускового тока, звезда, треугольник, схема запуска, видео, энергомагСкачать Что такое звезда и треугольник в трансформаторе?Скачать Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать Фильтрация токов НП через “треугольник” ТТСкачать Как работает пусковой переключатель со звезды на треугольникСкачать Поделиться или сохранить к себе: Смотрите также Площадь равнобедренного треугольника Площадь прямоугольного треугольника Плечо силы в треугольнике Плетение треугольника мозаичным плетением Плетение треугольника из лозы Плетение треугольника из веревки Плетение из газетных трубочек треугольник Плетение из бисера треугольник