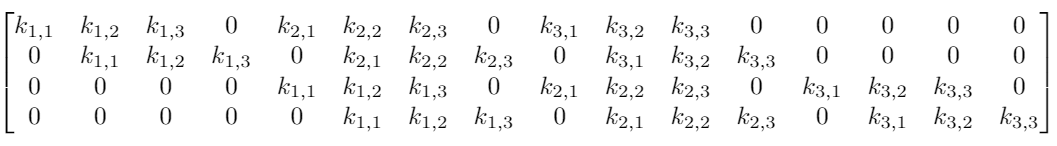Что такое свертка векторов (7 видео) | Курс школьной геометрии

Линейная и циклическая свертка

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Одним из китов современной техники, несомненно, является операция свертки:

Графически прохождение сигнала через фильтр c импульсной характеристикой , в соответствии с (1), показано на рисунке 1

В физически реализуемой системе реакция на входное воздействие не может наступить раньше самого воздействия, тогда импульсная характеристика должна быть равна нулю, при . Учитывая это свойство можно выражение (1) представить в виде:

Пусть имеется два дискретных сигнала , , , определенных на всем диапазоне индексов . Тогда линейной сверткой дискретных сигналов является вида:

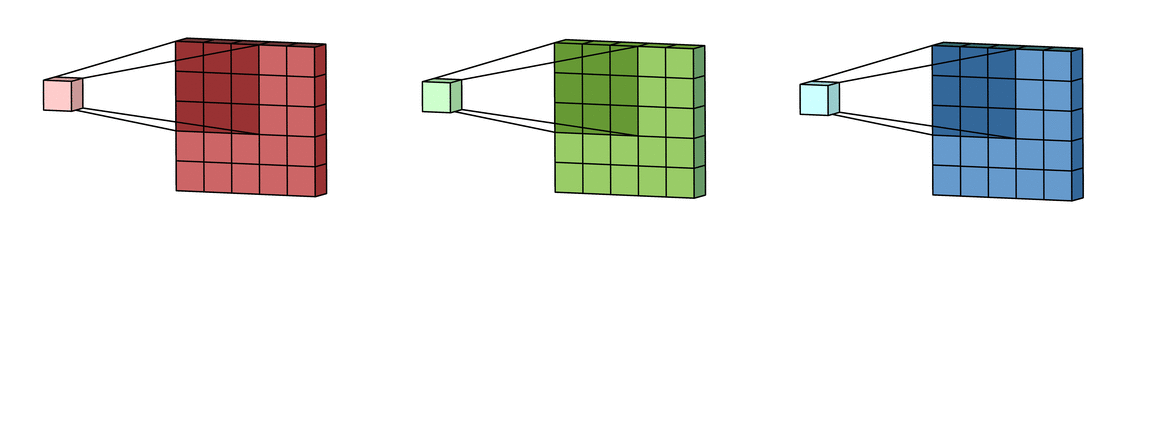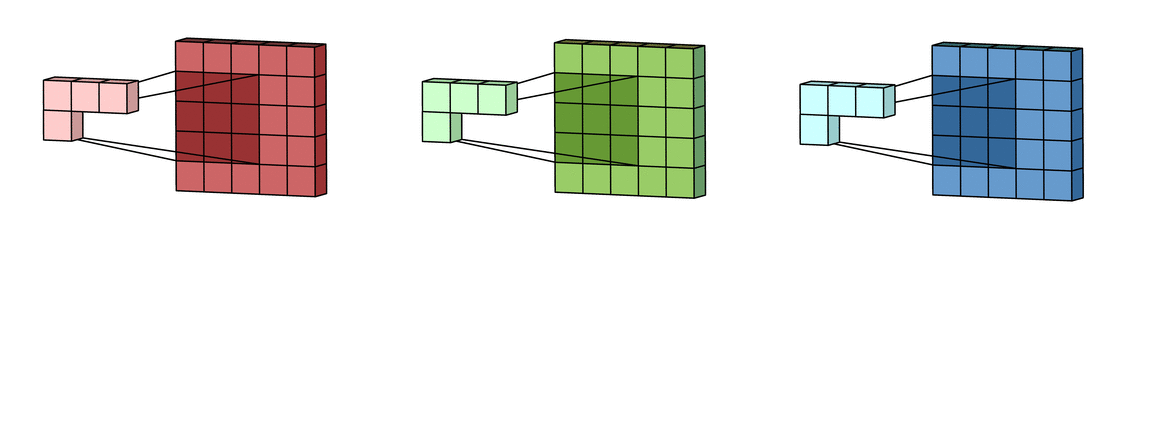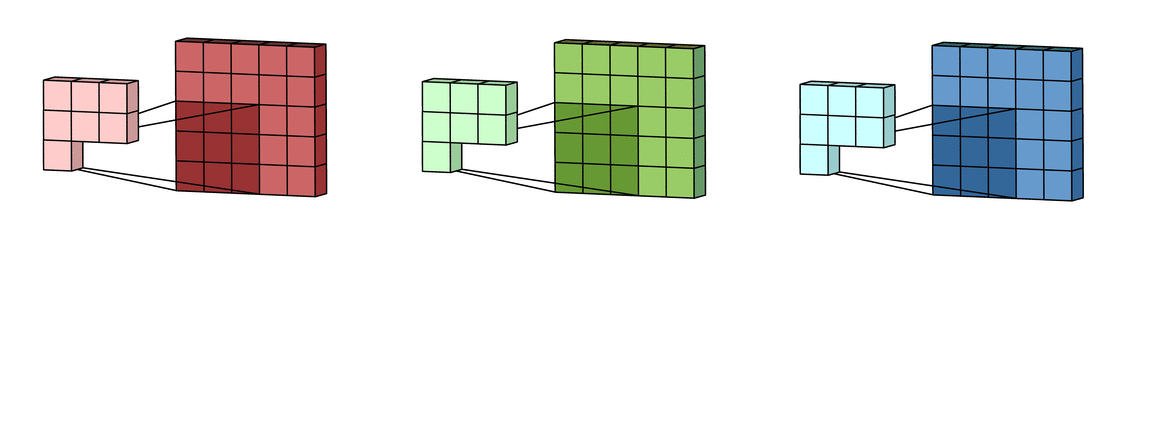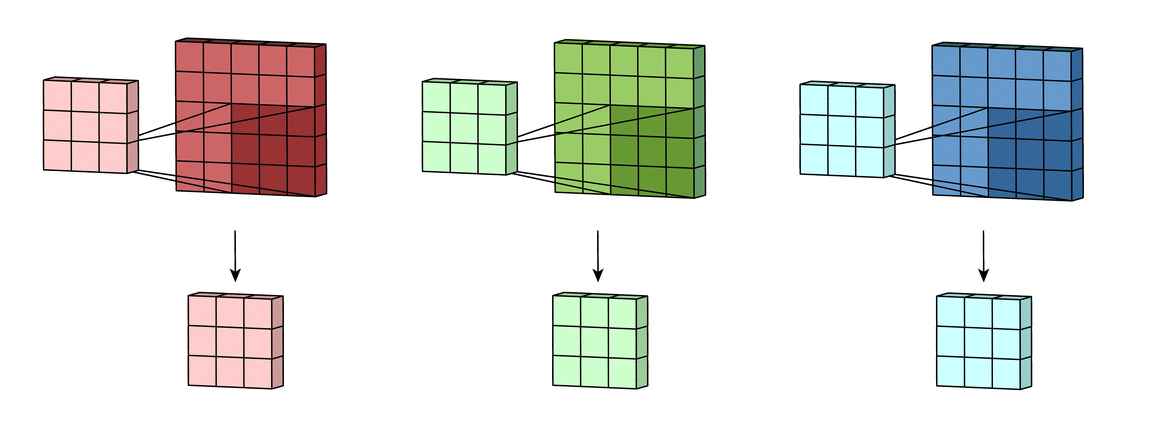
Для вычисления линейной свертки сигналы и и сдвигают относительно друг друга, все возможные перекрывающиеся отсчеты почленно перемножают и складывают как это представлено на рисунке 2.

Приведем пример вычисления линейной свертки. Пусть сигнал содержащий отсчета, а сигнал из отсчетов. Тогда процесс вычисления линейной свертки приведенных сигналов показан на рисунке 3.

Необходимо отметить, что сигнал при вычислении линейной свертки отражается слева-направо, поскольку — самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.

Линейная свертка описывает прохождение сигнала , через КИХ-фильтр порядка с импульсной характеристикой , :

Другим важнейшим прикладным значением линейной свертки является расчет произведения полиномов.

Пусть значения дискретной последовательности , , содержащей значение представляет собой коэффициенты полинома :

Пусть имеется выборка дискретного сигнала , длительности отсчетов, . Если мы возьмем последних отсчетов сигнала и перенесем их в начало, то получим сигнал , циклически задержанный относительно исходного на отсчетов. Для обозначения циклической задержки мы будет использовать обозначение , которая говорит о том, что разность берется по модулю , т.е. берется остаток от деления на .

Операции по модулю в предположении 0″/> выполняются по следующему правилам:

Пример циклической задержки сигналов показан на рисунке 4 для и .

Пусть имеется две последовательности и , одинаковой длительности отсчетов. Циклической сверткой называется последовательность вида:

Графически пример вычисления циклической свертки (9) для показан на рисунке 5.

Заметим, что вычисление циклической свертки можно представить в матричной форме:

Важнейшим свойством циклической свертки является то, что она сводится к произведению спектров ДПФ исходных последовательностей, а также к произведению их -образов. Использование аппарата быстрого преобразования Фурье обеспечивает высочайшую вычислительную эффективность циклических сверток.

Как мы знаем из свойств дискретного преобразования Фурье, ДПФ циклической свертки равно произведению спектров сворачиваемых сигналов:

Схематично процесс расчета циклической свертки сигналов и использованием алгоритмов быстрого преобразования Фурье показан на рисунке 6.

Заметим, что эффективность алгоритмов БПФ зависит от длины выборки . Наиболее эффективные алгоритмы разработаны для длины равной целой степени двойки (так называемые алгоритмы по основанию два). При этом помимо высокой вычислительной эффективности, алгоритмы БПФ по основанию два отличаются регулярными структурами при аппаратной и программной реализации, а также прекрасно распараллеливаются при мультипроцессорной обработке.

Например для , выполнение матричного умножения (10) наивным методом, без использования ускорений, потребует операции вещественного умножения. Если же мы применим алгоритм вычисления циклической свертки на основе БПФ, то потребуется три БПФ длины (обратное БПФ также считается через прямое), плюс 1024 комплексных умножения для поэлементного перемножения результатов БПФ.

Каждое из трех БПФ требует количество умножений равное:

Вычислительные преимущества, которые мы получаем при использовании аппарата БПФ для расчета циклической свертки, хотелось бы также получать и для расчета линейной свертки. С этой целью рассмотрим способ приведения линейной свертки последовательностей ограниченной длительности к циклической.

Пусть и — дискретные последовательности длительности и отсчетов соответственно. Линейная свертка последовательностей и вернет длительности отсчет. Если мы хотим получить как результат циклической свертки, то необходимо дополнить и до длины отсчет, как это показано на рисунке 7.

К последовательности необходимо добавить ноль, а к последовательности — ноль. такое добавление нулей обеспечит увеличение периодичности циклического буфера до размера, когда и перестанут перекрываться циклически. В результате циклическая свертка будет иметь вид:

Необходимо заметить, что добивать и нулями можно не только до длины , но и до любой длины . В результате вычисления циклической свертки дополненных нулями последовательностей до длины , первый значение на выходе будет представлять собой линейную свертку, а остальные значения будут нулевыми. Это можно использовать для дополнения исходных последовательностей нулями до длины, которая допускает использование эффективных БПФ алгоритмов.

Например при и , необходимо дополнить и нулями до длины . Однако мы можем дополнить их до длины отсчетов и использовать БПФ по основанию два для расчета циклической свертки. При этом первые 6999 отсчетов результата циклической свертки будут представлять собой линейную свертку при и . Использование алгоритма БПФ для приведет к десятикратному снижению требуемых вещественных умножителей при вычислении линейной свертки при и .

Таким образом, мы рассмотрели непрерывный интеграл свертки, который описывает реакцию линейного фильтра на произвольный входной сигнал.

Также было рассмотрено два вида дискретных сверток: линейная и циклическая, установлена связь между ними. Было показано, что применение БПФ обеспечивает существенное снижение вычислительных операций при вычислении как циклических, так и линейных сверток.

Содержание

Наглядно объясняем операцию свертки в моделях глубокого обучения
Суть операции свертки на примере черно-белых изображений
Некоторые распространенные методы
Нулевой отступ
Многоканальная версия – цветные изображения
Математическая подоплека свертки – особенности линейного преобразования
Локальность свертки
Визуализация признаков при помощи оптимизации
Зона восприимчивости свертки
Что такое свертка векторов
🎦 Видео

Видео:Свёртка двух функций. Или конволюция . Доступная иллюстрацияСкачать

Наглядно объясняем операцию свертки в моделях глубокого обучения

При помощи анимированных изображений и визуализаций слоев CNN-сетей раскрываем широко применяемое в моделях глубокого обучения понятие свертки.

В современных фреймворках глубокого обучения сверточные слои в моделях нередко представляются в виде однострочного кода. Само же понятие свертки обычно остается для начинающих аналитиков труднодоступным, как и лежащие в его основе понятия ядра, фильтра, канала и т. д. Тем не менее, свертка представляет собой мощный и расширяемый инструмент, позволяющий разреживать взаимодействия нейронов, находить общие параметры, работая одинаковым образом со входными данными различного размера. Сравним механики операции свертки и полносвязной нейросети.

Видео:Свертка двух функций. Найти свертку функций по определению. Теорема об умножении изображений.Скачать

Суть операции свертки на примере черно-белых изображений

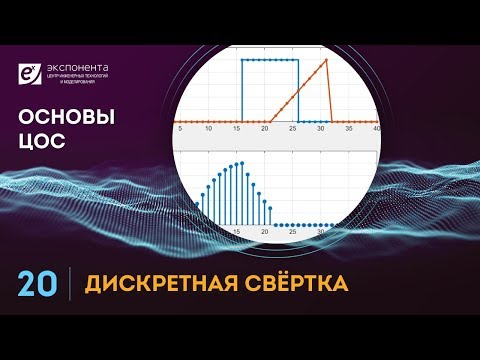
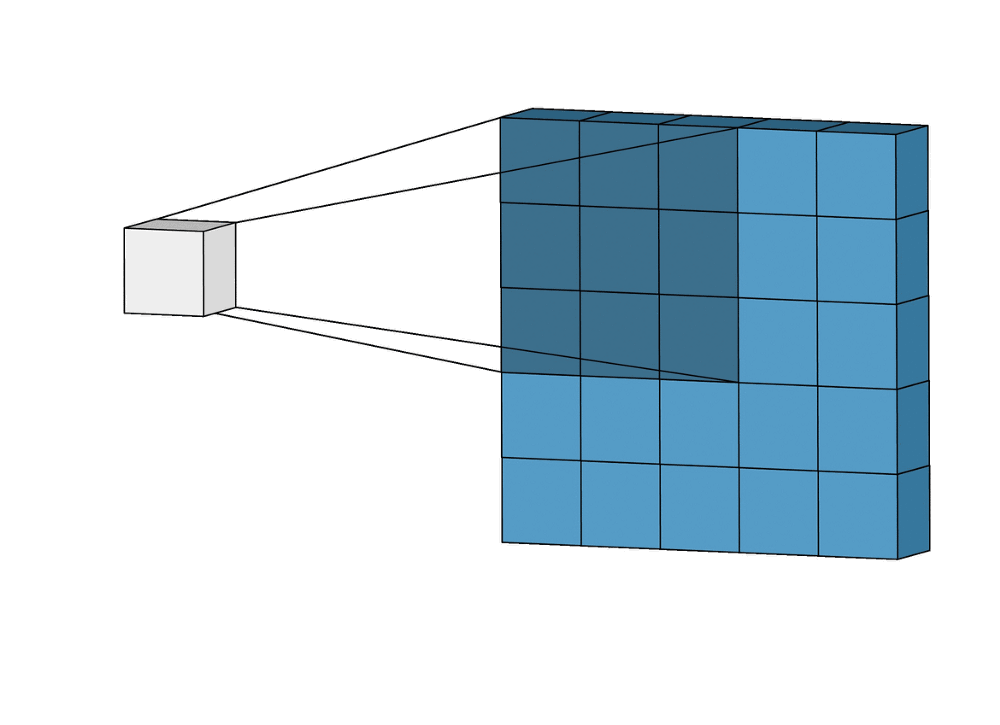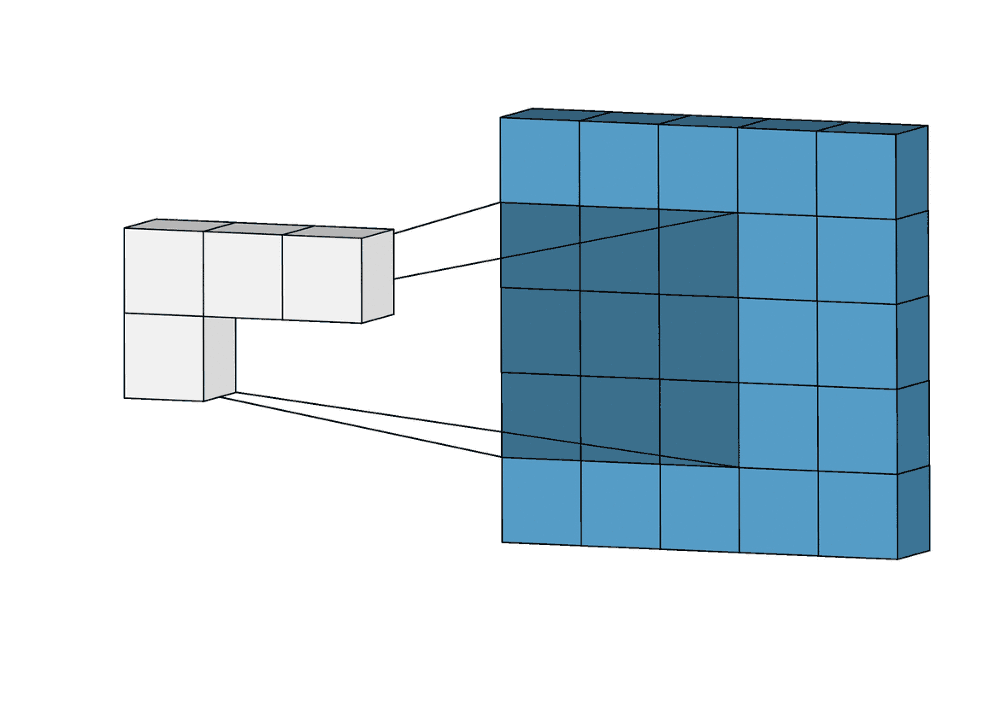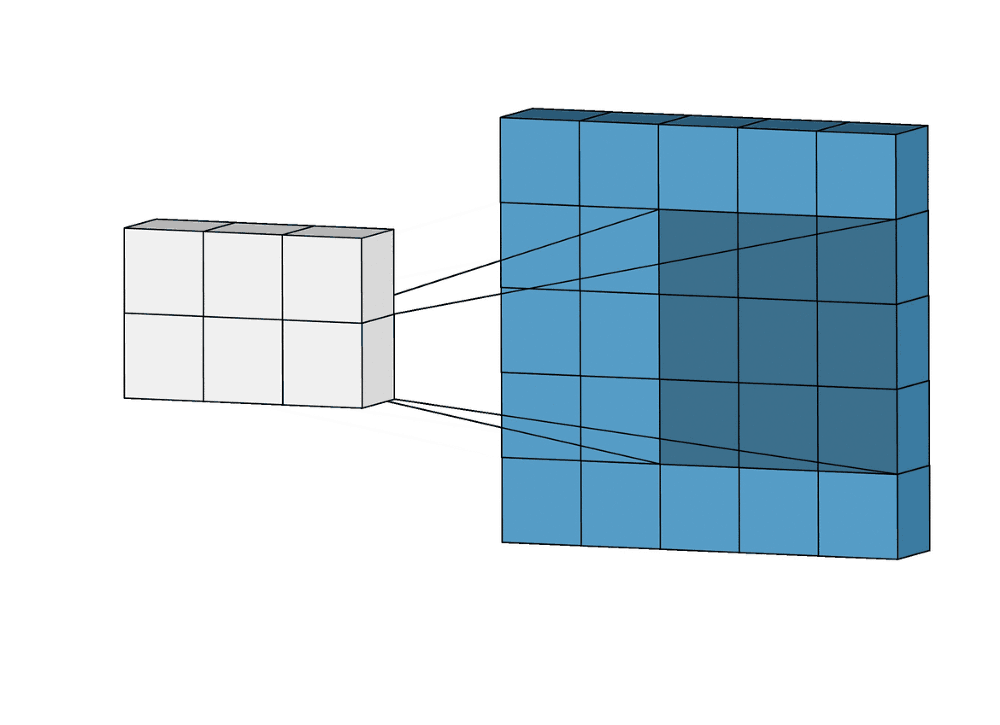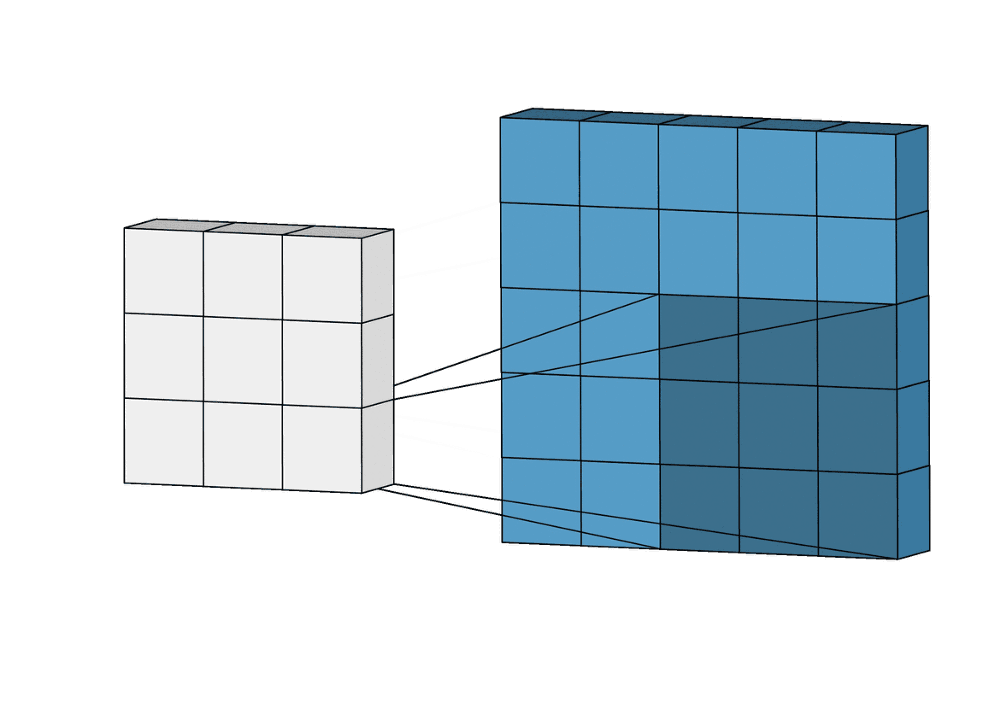
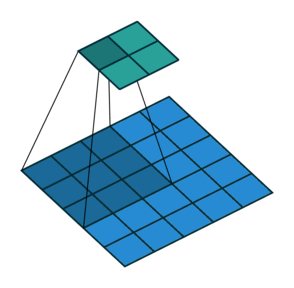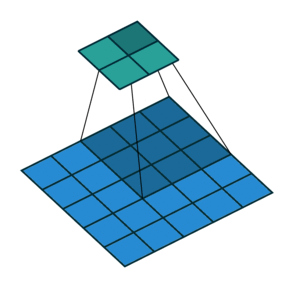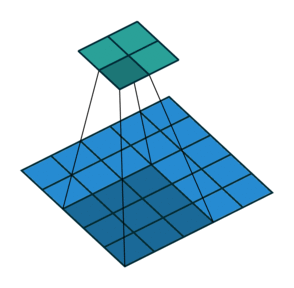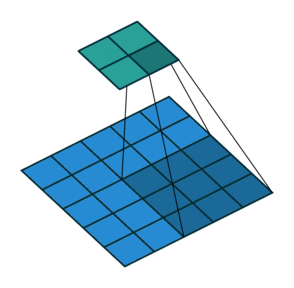
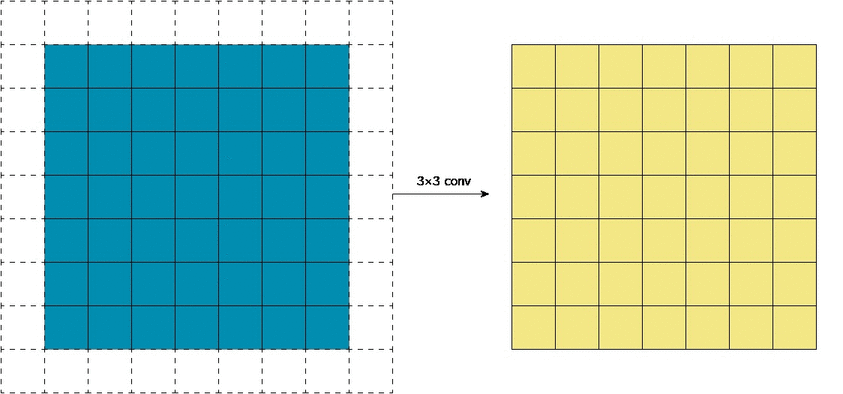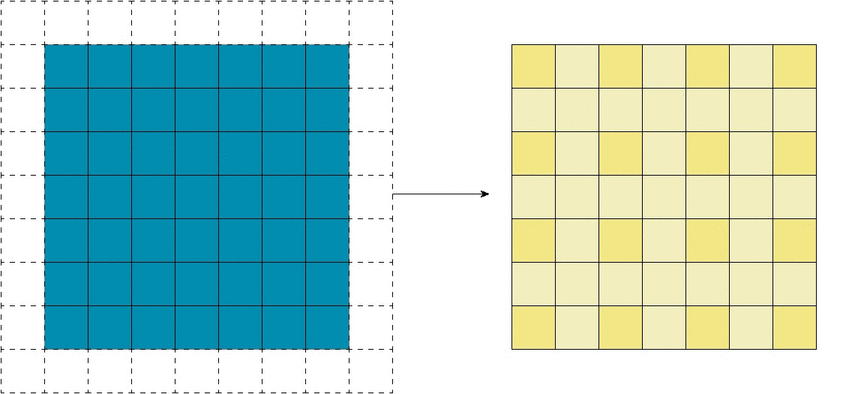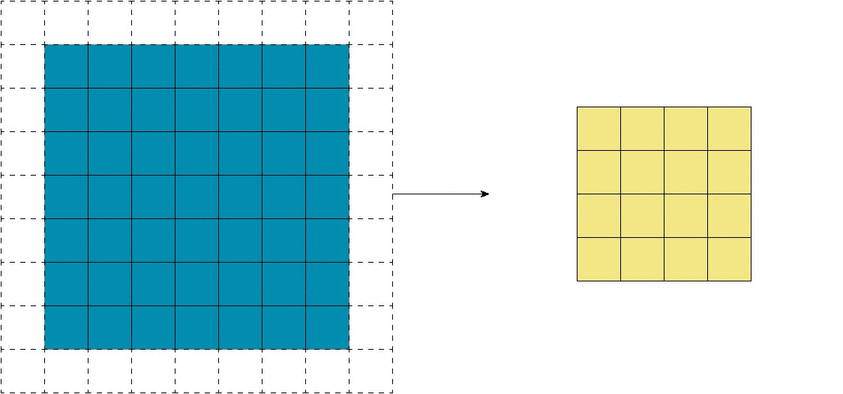
В математическом отношении в двумерной свертке нет ничего сложного. Имеется ядро – небольшая матрица весов. Это ядро «скользит» по двумерным входным данным, выполняя поэлементное умножение для той части данных, которую сейчас покрывает. Результаты перемножений ячеек суммируются в одном выходном пикселе. В случае сверточных нейросетей ядро определяется в ходе обучения сети. Начальные веса, аналогично случаю перцептрона, могут иметь рандомные значения, и корректируются в процессе обучения.

Перемножение и суммирование повторяются для каждой локации, по которой проходит ядро. Двумерная матрица входных признаков преобразуется в двумерную матрицу выходных. Выходные признаки, таким образом, являются взвешенными суммами входных признаков. Число входных признаков в комбинации для одного выходного признака определяет размер ядра.

Такой подход контрастирует с полносвязными сетями. Так, в приведенном выше примере имеется 5×5=25 входных признаков и 3×3=9 выходных. Если бы это были два полносвязных слоя, весовая матрица состояла бы из 25×9=225 весовых параметров. При этом каждая функция вывода была бы взвешенной суммой всех входов. В случае свертки, взвешенная сумма берется только по числу весов ядра. И в рассмотрении одновременно участвуют только близлежащие элементы.

Свертка соответствует модели иерархий абстрактных представлений: совокупность пикселей обобщается до ребер, те – до паттернов, и, наконец, до самого объекта. Малозначимые детали отфильтровываются в процессе перехода к более абстрактным образам.

Видео:ТЕНЗОРЫ ДЛЯ САМЫХ МАЛЕНЬКИХ ЧАЙНИКОВ (ДЛЯ ФИЗИКОВ)Скачать

Некоторые распространенные методы

Обратим внимание на два характерных метода, связанных с операцией свертки: дополнение отступа (padding) и выбор шага (strides).

Нулевой отступ

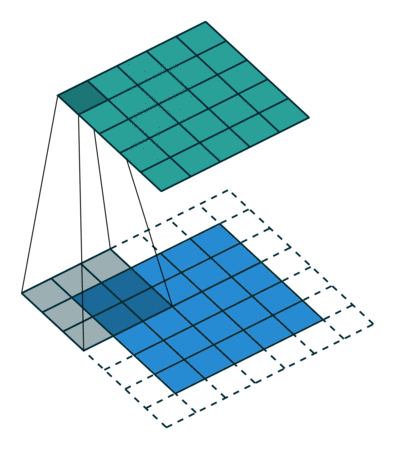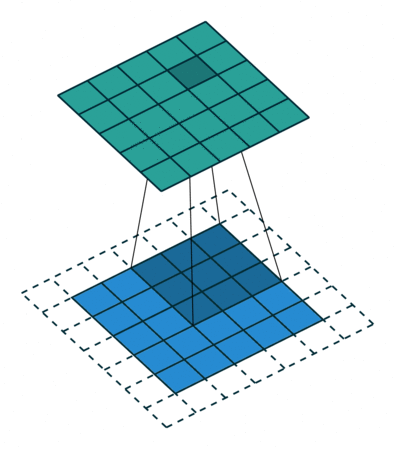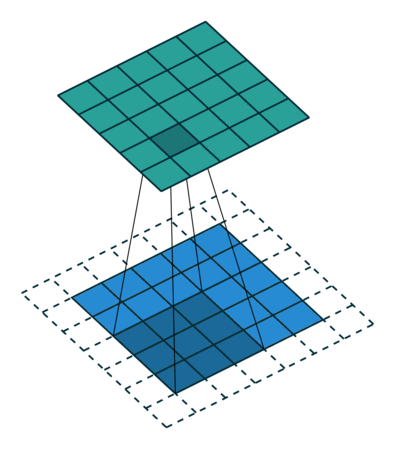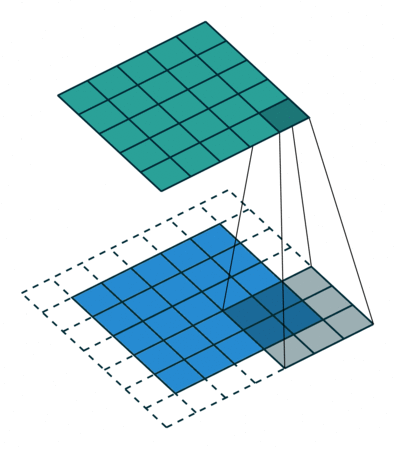
В вышеприведенном примере скольжение ядра «обрезает» исходный двумерный массив по краю, преобразуя матрицу 5×5 в 3×3. Краевые пиксели теряются из-за того, что ядро не может распространяться за пределы края. Однако иногда необходимо, чтобы размер выходного массива был тем же, что и у входных данных.

Чтобы решить эту задачу, исходный массив можно дополнить «поддельными» пикселями. Например, в виде краевого поля, окружающего массив. Если в качестве значений берутся нули, говорят о «нулевом отступе» (zero padding).

Еще чаще стоит задача субдискретизации – уменьшения размерности выходного сигнала в сравнении с исходным. Это обычное явление в сверточных нейросетях, где размер пространственных измерений уменьшается при увеличении количества каналов. Одним из способов является применение объединяющего (pooling) слоя. За счет отбора средних/максимальных значений из каждых соседствующих счетверенных ячеек 2×2 можно уменьшить размерность исходной сетки вдвое. Другой подход – использовать шаг свертки.

Идея шага состоит в том, чтобы при скольжении ядра пропускать часть позиций массива. Значения шага 1 означает выбор каждого пикселя сетки. Шаг 2 означает отбор пикселей на расстоянии в два пикселя с пропуском одного промежуточного, и так далее.

Видео:Свертка и подвыборкаСкачать

Многоканальная версия – цветные изображения

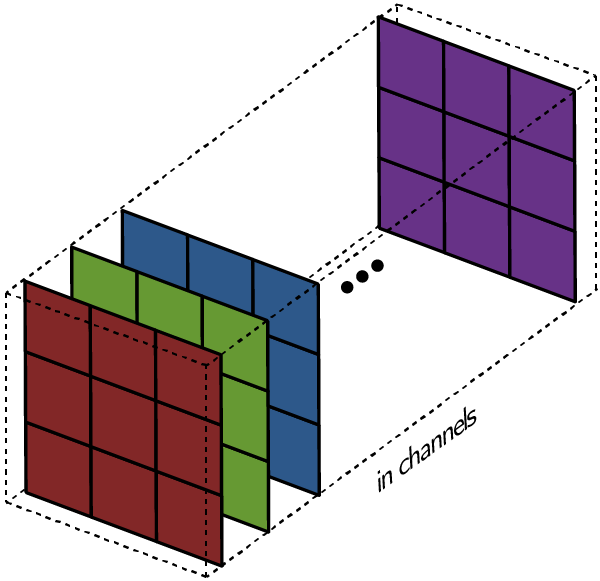
Вышеприведенные диаграммы соответствуют лишь изображениям с одним входным каналом. На практике большинство изображений имеют три канала: красный, зеленый и синий.

В случае с одним каналом термины фильтр и ядро взаимозаменяемы. Для цветного изображения они различны. Фильтр – это коллекция ядер, каждое из которых соответствует одному каналу. Ядро фильтра скользит по данным канала, создавая их обработанную версию. Значимость ядер определяется взаимным отношением их весов. Например, ядро для красного канала может быть более значимым в модели, чем другие ядра фильтра, тогда будут больше и соответствующие веса.

Каждая из обработанных в своих каналах версий суммируется для формирования общего канала.

В выходном терминале может присутствовать линейное смещение, независимое от функций каждого из ядер и свойственное лишь выходному каналу.

Видео:Что такое свёртка списка? Душкин объяснитСкачать

Математическая подоплека свертки – особенности линейного преобразования

Предположим, что у нас есть вход 4×4. Мы хотим преобразовать его в сетку 2×2. Если мы используем сеть прямого распространения, потребуется входной вектор из 16 нейронов, полностью связанных с 4 выходными нейронами. Такую ситуацию можно визуализировать весовой матрицей w.

Хотя операция ядерной свертки может показаться вначале немного странной, она является линейным преобразованием. Если бы мы использовали ядро K размера 3 для тех же размеров входа и выхода, эквивалентная матрица линейного преобразования выглядела бы следующим образом:

Для матрицы с 16×4=64 элементами имеется всего 9 нетривиальных параметров, подлежащих оптимизации вместо 64 весовых параметров для полносвязной двухслойной нейронной сети. Обнуление значительной части параметров обусловлено локальностью применяемой операции. Помимо ускорения расчетов, свертка приводит и к лучшей инвариантности относительно размеров входных данных.

Впрочем это не объясняет, почему такой подход может быть не менее эффективным, чем полносвязная сеть. Ядро, формирующее выходной сигнал, представляет взвешенную комбинацию небольшой области близкорасположенных пикселей. Но в то же время операция взаимодействия с ядром применяется одинаково ко всему изображению.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Локальность свертки

Если бы это был какой-то другой тип данных, а не изображения (например, набор категориальных данных), обобщение, осуществляемое сверткой, могло бы привести к катастрофе. В выходных признаках появлялась бы отсутствовавшая исходно корреляция.

В то же время любое изображение с точки зрения математики представляет собой совокупность правил взаимного расположения элементов. Использование фильтров для поиска элементов изображений – это одна из старых идей компьютерного зрения. Например, для обнаружения контуров можно использовать фильтр Собеля. В отличие от обучаемых ядер сверточных нейронных сетей, ядро этого фильтра имеет фиксированные веса:

Для фонового неба, не содержащего краевых элементов большинство пикселей на изображении имеют одинаковые значения. Суммарные значения выхода ядра в этих местах равны нулю. Для части изображения с вертикальными границами в местах границ существует разница между пикселями слева и справа от края. Ядро, вычисляя эту ненулевую разницу, определяет положение контуров. Повторимся, ядро работает каждый раз только с локальными областями 3×3, обнаруживая аномалии в локальном масштабе.

Применяя один и тот же подход ко всему изображению, можно получить результат для всего массива. Аналогично свертка с транспонированным ядром позволяет выделить горизонтальные края.

Видео:Интеграл свёртки: вывод формулы и её смыслСкачать

Визуализация признаков при помощи оптимизации

Целая отрасль исследований в сфере глубокого обучения посвящена тому, чтобы сделать модели нейронных сетей интерпретируемыми. Одним из мощных инструментов для подобного рода задач является предложенная в работе 2017 года визуализация признаков при помощи оптимизации. Идея в корне простая: оптимизировать изображение, инициализированное шумом, так, чтобы активировать фильтр как можно сильнее.

На трех изображениях ниже представлены визуализации трех различных каналов для первого сверточного слоя GoogleNet. Хотя слои детектируют различные типы контуров, все они являются низкоуровневыми детекторами.

На двух следующих изображениях представлены примеры визуализации фильтров сверточных слоев второго и третьего уровней.

Одна из важных вещей: изображения после операции свертки – это все еще изображения. Операция действует эквивариантно: если изменяется вход, то выход изменяется так же.

Элементы, находившиеся в левом верхнем углу, после свертки имеют соответствующие отображения также в левом верхнем углу. Как бы глубоко ни заходили детекторы признаков, они все равно будут работать на очень маленьких ядерных участках. Неважно, насколько глубоко происходит свертка, но вы не можете обнаружить лица из сеток размером 3х3. Здесь возникает идея локальной зоны восприимчивости (receptive field).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Зона восприимчивости свертки

Существенной составляющей архитектуры сверточной нейронной сети является уменьшение объема данных от входа к выходу модели с одновременным увеличением глубины канала. Как упоминалось ранее, обычно это делается при помощи выбора шага свертки или pooling-слоев. Зона восприимчивости определяет, какая площадь оригинальных входных данных из исходной сетки обрабатывается на выходе. На изображениях ниже представлен пример шагающей свертки с выкидыванием промежуточных пикселей.

Ниже представлены примеры визуализации признаков набора блоков свертки, показывающие постепенное увеличение сложности. Расширение поля восприимчивости позволяет сверточным слоям комбинировать низкоуровневые признаки (линии, края) в более высокоуровневые (кривые, текстуры).

Сеть развивается от небольшого количества низкоуровневых фильтров на начальных этапах (64 в случае GoogleNet) до очень большого количества фильтров (1024 в финальной свертке), каждый из которых находит специфичный высокоуровневый признак. Переход от уровня к уровню обеспечивает иерархию распознавания образов.

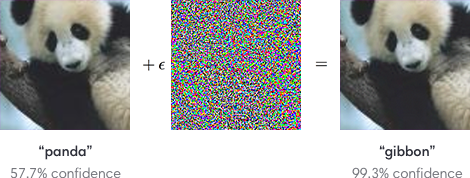
Обобщающие процессы свертки имеет свою оборотную сторону – возможность подделки изображений под удовлетворение особенностей распознающих фильтров. На изображениях ниже человек в обоих случаях узнает фотографии панды. А сверточные нейросети можно запутать, добавив шум, подстроенный под фильтры распознавания других образов.

Однако именно сверточные нейронные сети позволили компьютерному зрению пройти путь от простых приложений до сложных продуктов и услуг, таких как распознавание лиц и улучшение качества медицинских диагнозов.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Что такое свертка векторов

Все заявки обрабатываются в порядке живой очереди в режиме неонлайн в течение суток. Техническая поддержка сайта: 521-242

На сайте используется два типа cookies:

Основным является сессионный cookie, обычно называемый MoodleSession. Вы должны разрешить использование этого файла cookie в своем браузере, чтобы обеспечить непрерывность и оставаться в системе при просмотре сайта. Когда вы выходите из системы или закрываете браузер, этот файл cookie уничтожается (в вашем браузере и на сервере).

Другой файл cookie предназначен исключительно для удобства, его обычно называют MOODLEID или аналогичным. Он просто запоминает ваше имя пользователя в браузере. Это означает, что когда вы возвращаетесь на этот сайт, поле имени пользователя на странице входа в систему уже заполнено для вас. Отказ от этого файла cookie безопасен — вам нужно будет просто вводить свое имя пользователя при каждом входе в систему.

Некоторые курсы, возможно, открыты для гостей