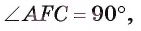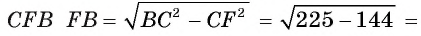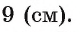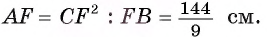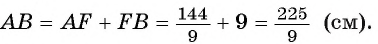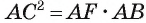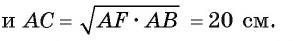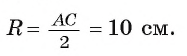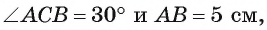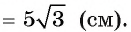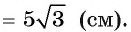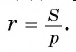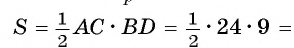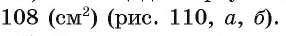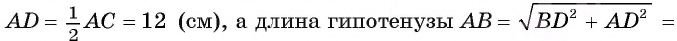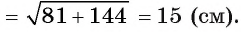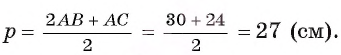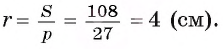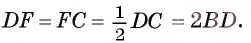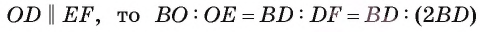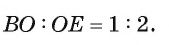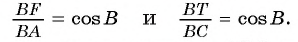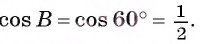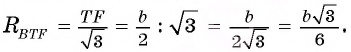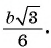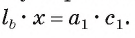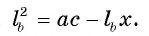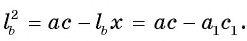Как решить задачу с треугольником в окружности (5 видео)

Треугольник вписанный в окружность

Содержание

Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Как решить задачу с треугольником в окружности
Треугольники и окружность — задачи с примерами решения
📺 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Как решить задачу с треугольником в окружности

Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.

а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.

б) Найдите площадь треугольника АСВ.

а) Введём обозначения, как показано на рисунке, пусть M, H, N — точки касания. Касательные, проведённые к окружности из одной точки равны: AM = AN, CM = CH, HB = BN. Поэтому:

откуда p = AM, где Р — периметр, p — полупериметр треугольника.

б) Для определения площади треугольника используем формулу, связывающую её с полупериметром, стороной и радиусом вневписанной окружности, касающейся этой стороны и продолжений двух других сторон треугольника:

Ответ:

Примечание: указанная в решении формула легко может быть получена из следующих соображений где O₁ — центр окружности с радиусом r_1. При этом

Тогда

В остроугольном треугольнике ABC проведены высоты AP и CQ.

а) Докажите, что угол PAC равен углу PQC.

б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что PQ = 8 и ∠ABC = 60°.

а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC, и, следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC, что и требовалось доказать.

б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC, следовательно, они подобны, откуда или но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен откуда Тогда радиус R окружности, описанной около треугольника ABC равен

Ответ:

В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и ∠KMN = 45°.

а) Углы NAK и NBK, опирающиеся на отрезок KN, равны, значит, точки A, B, N и K лежат на одной окружности, а, следовательно, равны и вписанные углы ABK и ANK этой окружности, опирающиеся на дугу AK, что и требовалось доказать.

б) Прямоугольные треугольники KMB и NMA имеют общий угол KMN, следовательно, они подобны, откуда или но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен откуда

Тогда радиус R окружности, описанной около треугольника ABM равен

Ответ:

Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.

а) Докажите, что четырехугольник ABKC вписанный.

б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.

а) Пусть Так как — центр вписанной окружности треугольника ABC, то — биссектрисы углов и значит, Угол BOK внешний для треугольника AOB, поэтому (см. рисунок).

Так как (по построению), то тогда Углы CBK и KAC опираются на один и тот же отрезок CK и равны друг другу: Тогда по признаку, связанному со свойством вписанных углов, точки лежат на одной окружности.

б) Обозначим через радиусы вписанной и описанной окружностей треугольника Пусть H — проекция точки O на сторону AB (см. рис.), тогда Так как точки лежат на одной окружности, то радиус описанной окружности треугольника ABK совпадает с радиусом описанной окружности треугольника и равен Из треугольника ABK по теореме синусов: Тогда

Так как то

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Треугольники и окружность — задачи с примерами решения

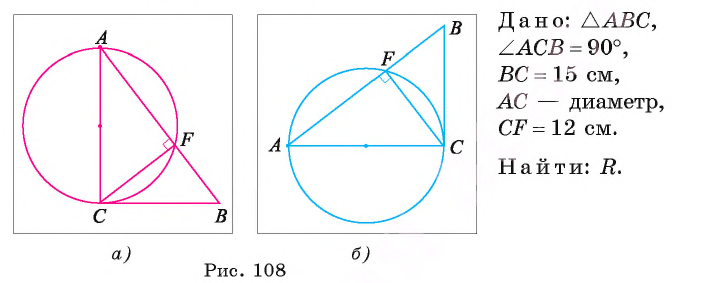
Пример:

Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.

Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что

1) В треугольнике

2) Воспользовавшись равенством 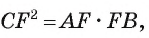найдем

3) Теперь

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,

Таким образом,

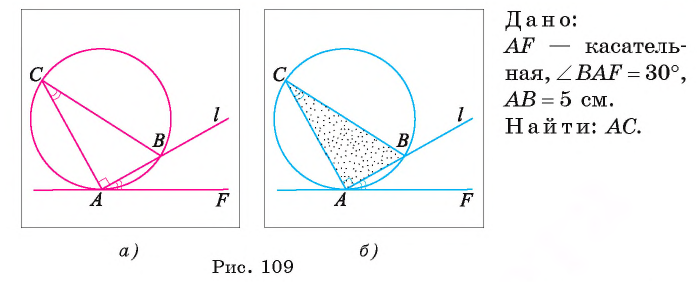
Пример:

Решение:

По теореме об угле между хордой и касательной 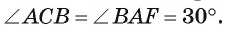Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как

Ответ

Пример:

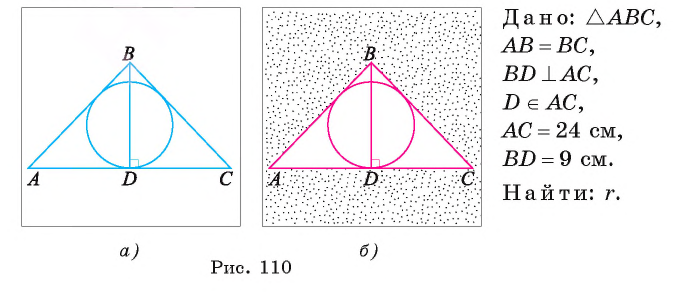
Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 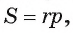где S — площадь треугольника, р — его полупериметр. Отсюда получим

1) Площадь треугольника

2) В прямоугольном треугольнике ADB длина катета

3) Теперь полупериметр

4) Таким образом, найдем

Пример:

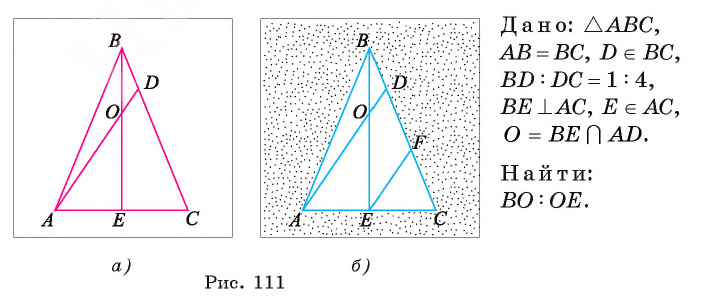
В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 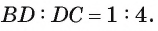В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

Решение:

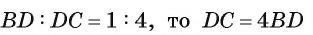
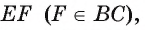
1) Так как (рис. 111, а, б). Проведем отрезок , параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,

4) Так как

Ответ:

Пример:

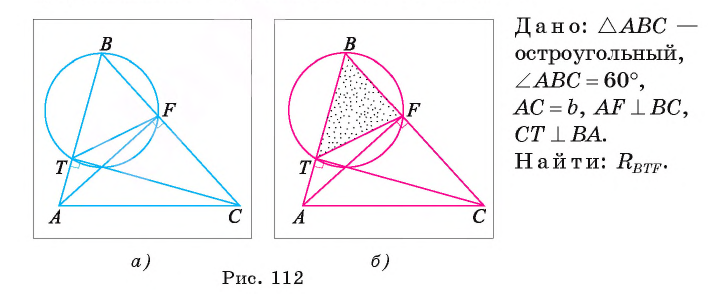
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.

Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

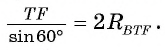
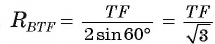
1) В треугольнике BTF по теореме синусов выполняется равенствоСледовательно, (рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,

Следовательно,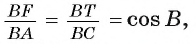т.е. треугольники подобны с коэффициентом подобия

3) Из подобия треугольников ABC и FTC следует, что 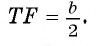Таким образом,

Ответ:

Пример:

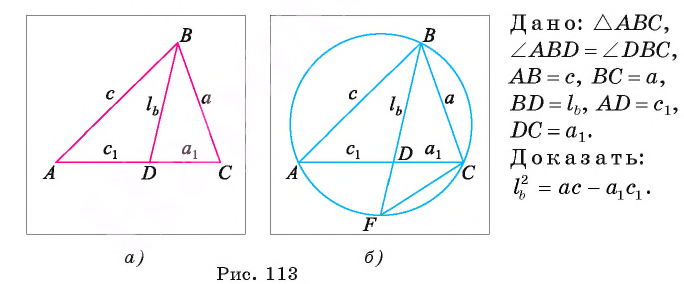
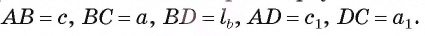
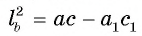
Отрезок BD — биссектриса треугольника ABC. Известно, что Докажите, что (рис. 113, а).

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство

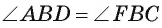
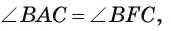
2) Треугольники ABD и FBC подобны, так как по условию и поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что 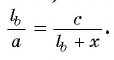Отсюда

3) Таким образом,

Что и требовалось доказать.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Площадь треугольника
Соотношения между сторонами и углами произвольного треугольника
Окружность и круг
Описанные и вписанные окружности
Пространственные фигуры — виды, изображения, свойства
Взаимное расположения прямых на плоскости
Треугольник
Решение треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.