Что общего у сферы и окружности (2 видео)

Отличие окружности и круга

Частное учреждение профессионального образования

«Юридический полицейский колледж»

Реферат

на тему: «Круг, окружность, шар, сфера их отличия»

Студентка группа 18ПД

Проверил: Щербаков К.В.

В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего.

Окружность– это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.

Окружность имеет центр — это начальная точка нарисованная циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.

Круг– является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.

Отличие окружности и круга

Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр.

Пример: Таким образом, круг является некоторым участком плоскости, а окружность — всего лишь граница этого участка. Чтобы лучше понять это, представьте себе кольцо (я возьму что-нибудь круглое и съедобное, например, бублик). Это и будет нашей окружностью. Бублик имеет дырочку. Дырочка к бублику не относится, дырочку от бублика съесть нельзя, а вот сам бублик можно кушать. Понимаете? Всё, что лежит внутри окружности, к самой окружности не относится (за исключением окружности с нулевым радиусом). Теперь мысленно вставим в бублик круглую булочку, так, чтобы булочка идеально вписалась в бублик (чтобы не было зазоров и проч.). Булочка и бублик образуют круг. Бублик будет границей этого круга, частью круга (бублик принадлежит кругу, а так как за бублик мы взяли окружность, то окружность принадлежит кругу). И булочку, и бублик можно съесть. Пример с бубликом и булочкой является самым наглядным примером, который при желании можно повторить дома, хотя здесь достаточно всё представить мысленно.

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).

В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сфер это условие не является обязательным.

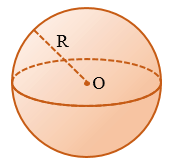
Пример: Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.

Содержание

Окружность, круг, шар
Основные характеристики окружности
Построение окружности
Шар и сфера
Определение
Математика. 5 класс
🔥 Видео

Видео:Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать

Окружность, круг, шар

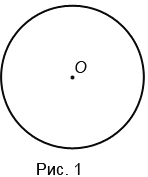
Окружность — это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О — центр окружности.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Основные характеристики окружности

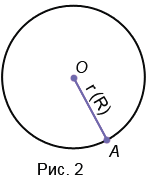
1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.

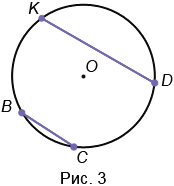
2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.

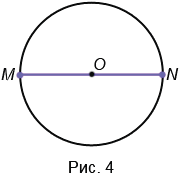
3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.

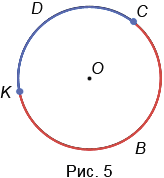
4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.

Видео:Площадь сферыСкачать

Построение окружности

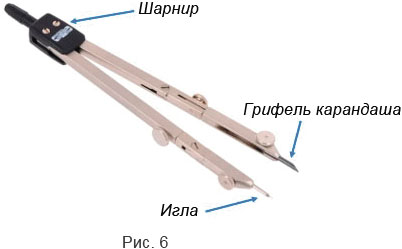
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.

Выполнение построения:

отмечаем точку, которая будет центром окружности;
делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);

ставим иглу циркуля в точку, которая определяет центр окружности;
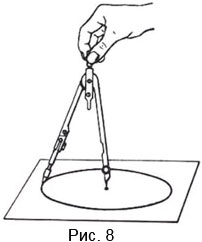
проводим окружность данного радиуса (Рис.8).

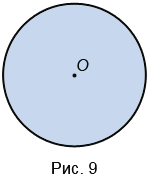
Часть плоскости, которая лежит внутри окружности (вместе с самой окружностью), называют кругом (Рис.9).

Шар и сфера

Сфера — поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Центр сферы — данная точка (точка О на рисунке выше).

Радиус сферы — данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы — R, то ее диаметр — 2R.

Определение

Шар — тело, ограниченное сферой.

Поделись с друзьями в социальных сетях:

Видео:11 класс, 19 урок, Сфера и шарСкачать

Математика. 5 класс

Конспект урока

Окружность и круг. Сфера и шар

— понятия «окружность», «круг», «сфера», «шар» и их элементы;

— изображение окружности на плоскости, сферы в пространстве.

Окружность – это плоская замкнутая кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки – её центра.

Круг – плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра).

Центр окружности – это точка, равноудалённая от точек окружности.

Радиус окружности – это отрезок, соединяющий какую-нибудь точку этой окружности с её центром.

Хорда окружности – это отрезок, соединяющий какие-нибудь две точки окружности.

Диаметр окружности – это хорда, проходящая через центр окружности.

Шар – это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Ещё в глубокой древности люди изобрели колесо, придумали гончарный круг, сделали украшения в виде колец, то есть создали предметы, в основе которых лежит окружность или круг. В современных устройствах эти геометрические фигуры тоже встречаются очень часто. Сегодня мы поговорим не только о том, как они используются в наше время, но и выясним их отличие друг от друга.

Итак, что же такое окружность?

Окружность – это замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Эта точка называется центром окружности.

Построим окружность. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки отрезок длиной 3 см. Поставим иголку циркуля в точку О и начертим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую линию, которую называют окружностью. Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, то есть окружность есть граница круга.

При построении окружности расстояние между ножками циркуля не меняется. Поэтому все точки окружности равно удалены от точки О. Точку O называют центром и окружности, и круга. Отметим на окружности любую точку – например, точку L. Построим отрезок, соединяющий точку L с центром окружности – точкой О.

Отрезок ОL называют радиусом окружности.

Отметим на окружности любые две точки. Например, C и D. Построим отрезок, соединяющий точки C и D.

Отрезок CD называют хордой окружности. Некоторые хорды окружности проходят через её центр. Например, хорда AB проходит через центр окружности. Такую хорду называют диаметром окружности. То есть АВ – диаметр окружности.

Концы диаметра делят окружность на две равные части. Длина диаметра окружности равна двум радиусам. Две точки делят окружность на две части, называемые дугами. Например, CD. Обычно рассматривается одна из дуг окружности, определяемая по смыслу задачи.

Окружность разбивает плоскость на две части – внутреннюю область и внешнюю.

Давайте представим себе яблоко и воздушный шарик.

Чем они отличаются друг от друга?

Они оба имеют форму шара. Однако воздушный шарик полый внутри. Для таких предметов в математике есть название – сфера. А яблоко, с точки зрения математиков, – это шар.

Шар–это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Отрезок, соединяющий точку поверхности шара с его центром, называется радиусом шара.

Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.

Поверхность шара называется сферой.

Окружность и круг являются плоскими фигурами, то есть такими, которые располагаются в пределах одной плоскости. Такие фигуры – это не что иное, как рисунки на листе бумаги. Рассмотренные на уроке сфера и шар относятся к пространственным телам. Между сферой, шаром, окружностью и кругом есть взаимосвязь. Сфера и шар образуются вращением вокруг оси окружности и круга соответственно.

Легенда о циркуле

В жизни для построений мы используем различные инструменты. Так, для того чтобы нарисовать окружность, необходим циркуль. Но как появился циркуль? Обратимся к мифам Древней Греции.

В далёкие времена в Афинах жил юноша, которого звали Талос. Он с детства был очень талантлив. В 12 лет он изобрёл гончарный круг для изготовления посуды. Также он придумал первую пилу, обратив в живой природе внимание на то, что скелет рыбы напоминает острые зубья. И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.

№ 1. Подпишите соответствующие элементы окружности.

Вспомним определения радиуса (это отрезок, соединяющий какую-нибудь точку этой окружности с её центром), хорды (это отрезок, соединяющий какие-нибудь две точки окружности), диаметра (это хорда, проходящая через центр окружности) и ценрта окружности (это точка, равноудалённая от точек окружности).

О – центр окружности.

№ 2. Выберите правильный ответ.

Рассмотрим отрезок АК, длина которого равна 8см. Построено две окружности: первая – с центром в точке A, а вторая – с центром в точке К. Их радиусы, соответственно, равны 4 см и 6 см. Сколько общих точек имеют окружности?

Решение: чтобы ответить на вопрос, изобразим отрезок и окружности.