Четырехугольник mnkp вписан в окружность угол mnp равен 81

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Решение №216 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 110 градусов, угол ABD равен 70 градусов.

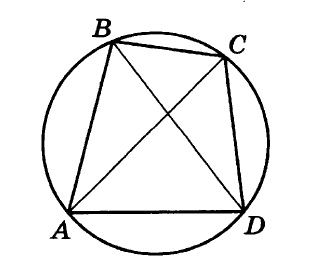
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 110 градусов, угол ABD равен 70 градусов. Найдите угол CAD. Ответ дайте в градусах.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Решение

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Задача по геометрии (просто) Найдите углы четырехугольника MNKP, вписанного в

Задача по геометрии (просто)

Найдите углы четырехугольника MNKP, вписанного в окружность, если lt;MKP=58* , lt;MPN=34*, lt;KMP=16*.

*-градусы

Пожалуйста, поподробнее, а так же если не трудно с рисунком.

• Damanov Igor
• Геометрия 2018-12-14 15:58:29 1 1

угол NРК = 180 — (угол КМР + угол МРN + угол МКР) = 72

угол Р = угол МРN + угол NPK = 34+72 = 106

угол N = 180 — угол Р = 180 — 106 = 74 (сумма противоположных углов вписанного четырехугольника одинакова 180)

угол NМК = угол NPK = 72 — (как углы, опирающиеся на одну дугу)

угол М = угол NMK + угол КМР = 72+16 = 88

угол К = 180 — угол М = 180 — 88 = 92 (сумма обратных углов вписанного четырехугольника одинакова 180)

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность

С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.

Видео:Вписанный в окружность четырёхугольник.Скачать

Общие понятия

Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.

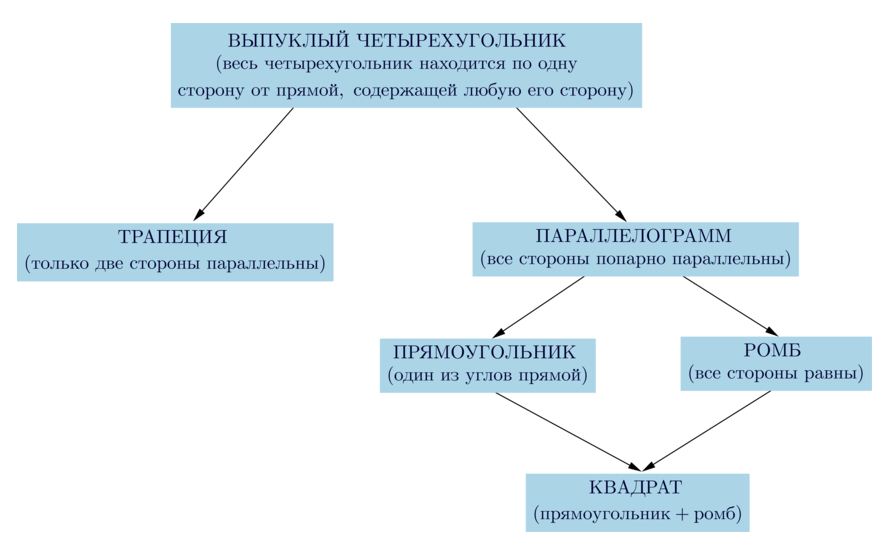
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.

Четырехугольник может быть следующих видов:

• Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
• Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
• Прямоугольник. Фигура, у которой все 4 угла = 90º.
• Ромб. Фигура, у которой все стороны равны.
• Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.

Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.

Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Частные случаи

Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:

• Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
• Если все вершины ромба находятся на описывающей линии, то он является квадратом.
• Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.

Видео:Вписанные четырехугольники. 9 класс.Скачать

Свойства вписанного четырехугольника в окружность

Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Теорема 1

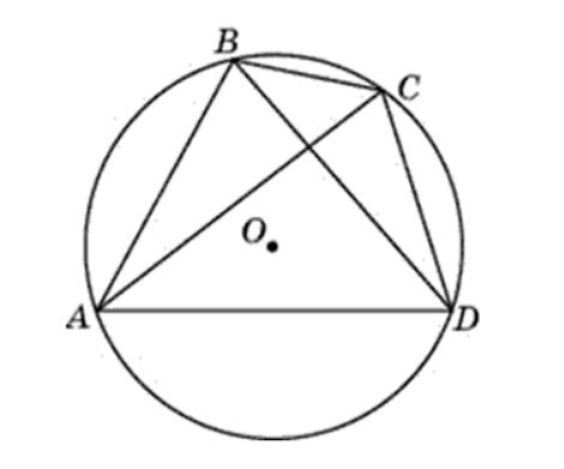
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.

Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что _{18 ноября, 2018}

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Решение №216 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 110 градусов, угол ABD равен 70 градусов.

Четырёхугольник ABCD вписан в окружность. Угол ABC равен 110 градусов, угол ABD равен 70 градусов. Найдите угол CAD. Ответ дайте в градусах.

Видео:Задание 24 ОГЭ по математике #7Скачать

Решение

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Задача по геометрии (просто) Найдите углы четырехугольника MNKP, вписанного в

Задача по геометрии (просто)

Найдите углы четырехугольника MNKP, вписанного в окружность, если lt;MKP=58* , lt;MPN=34*, lt;KMP=16*.

*-градусы

Пожалуйста, поподробнее, а так же если не трудно с рисунком.

• Damanov Igor
• Геометрия 2018-12-14 15:58:29 1 1

угол NРК = 180 — (угол КМР + угол МРN + угол МКР) = 72

угол Р = угол МРN + угол NPK = 34+72 = 106

угол N = 180 — угол Р = 180 — 106 = 74 (сумма противоположных углов вписанного четырехугольника одинакова 180)

угол NМК = угол NPK = 72 — (как углы, опирающиеся на одну дугу)

угол М = угол NMK + угол КМР = 72+16 = 88

угол К = 180 — угол М = 180 — 88 = 92 (сумма обратных углов вписанного четырехугольника одинакова 180)

📹 Видео

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия 8 класс (Урок№27 - Теорема о вписанном угле.)Скачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Описанные четырехугольники. 9 класс.Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать