Четырехугольник abcd основание пирамиды sabcd постройте прямую пересечения плоскостей asb и csd

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

МАТЕМАТИКА ЕГЭ. Под редакцией И. В. Ященко. профильный уровень ЗАДАЧА 14. Р. К. Гордин ГЕОМЕТРИЯ. СТЕРЕОМЕТРИЯ

Наталия Мисюрёва 4 лет назад Просмотров:

1 МАТЕМАТИКА 2017 Под редакцией И. В. Ященко ЕГЭ профильный уровень ЗАДАЧА 14 Р. К. Гордин ГЕОМЕТРИЯ. СТЕРЕОМЕТРИЯ

2 ГОТОВИМСЯ К ЕГЭ Р. К. Гордин ЕГЭ Математика Геометрия. Стереометрия Задача 14 (профильный уровень) Под редакцией И. В. Ященко Издание соответствует новому Федеральному государственному образовательному стандарту (ФГОС) Электронное издание Москва Издательство МЦНМО 2017

3 ББК 22.1я72 Г68 Гордин Р. К. ЕГЭ Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / Под ред. И. В. Ященко. Электронное издание. М.: МЦНМО, с. ISBN Пособия по математике серии «ЕГЭ Математика» ориентированы на подготовку учащихся старшей школы к успешной сдаче единого государственного экзамена по математике. В данном учебном пособии представлен материал для подготовки к решению задачи 14 профильного уровня. На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по стереометрии. Пособие предназначено для учащихся старшей школы, учителей математики, родителей. Издание соответствует новому Федеральному государственному образовательному стандарту (ФГОС). Подготовлено на основе книги: Гордин Р. К., ЕГЭ Математика. Геометрия. Стереометрия. Задача14 (профильный уровень) / Под ред. И. В. Ященко. М.: МЦНМО, с. ISBN Издательство Московского центра непрерывного математического образования , Москва, Большой Власьевский пер., 11, тел. (499) ISBN Гордин Р. К., МЦНМО, 2017.

4 Предисловие Это учебное пособие предназначено для подготовки к решению задачи 14 ЕГЭ по математике на профильном уровне. Предполагается, что школьник освоил школьный курс стереометрии с оценкой не ниже 4. Перед работой с этим задачником необходимо повторить основные определения и теоремы из школьного учебника. Это полезно делать и в процессе работы с пособием. Пособие начинается с основных сведений о многогранниках. В первом параграфе собраны задачи, связанные с изображением пространственных фигур на плоскости и построением сечений многогранников. Следующие восемь параграфов содержат методы решения задач на доказательство и вычисление по стандартным темам ЕГЭ: угол между прямыми, угол между плоскостями, расстояния от точки до прямой и до плоскости, угол между прямой и плоскостью, расстояние между прямыми, площадь сечения, объёмы, фигуры вращения. Каждый параграф начинается с повторения теории и нескольких примеров решения задач. Затем идут подготовительные задачи для самостоятельного решения. Как правило, эти задачи взяты из пособия В. А. Смирнова «Задача С2», издававшегося в предыдущие годы. Далее расположены задачи на доказательство (или на построение) и вычисление. В 10 рассматриваются задачи на вычисление элементов правильных пирамид и задачи повышенной трудности (задачи со звёздочкой). В приложении рассматриваются примеры решения стереометрических задач методом координат. Пособие завершают шесть диагностических работ, каждая из которых содержит по шесть задач, расположенных по возрастанию сложности. Если школьник решает четыре задачи за два часа, это можно считать вполне хорошим результатом.

5 Краткий список основных сведений о многогранниках Диагональю многогранника называется отрезок, соединяющий две вершины, не лежащие в одной грани. n-угольной призмой называется многогранник, две грани которого равные n-угольники, лежащие в параллельных плоскостях (основания), а остальные n граней (боковые грани) параллелограммы. Призма называется прямой, если её боковые рёбра перпендикулярны плоскости основания. В противном случае призма называется наклонной. Во всех задачах, связанных с призмой, будем считать, что AA 1, BB 1, боковые рёбра призмы AB A 1 B 1 Прямая призма называется правильной, если её основание правильный многоугольник. Параллелепипедом называется призма, основание которой параллелограмм. Противоположные грани параллелепипеда попарно равны и параллельны. Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны плоскости основания. Параллелепипед называется прямоугольным, если все его грани прямоугольники. Длины трёх рёбер, исходящих из одной вершины, называются измерениями прямоугольного параллелепипеда. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. Куб это прямоугольный параллелепипед с равными измерениями. n-угольной пирамидой с вершиной S называется многогранник SA 1 A n, грань A 1 A 2 A n которого n-угольник (основание пирамиды), а остальные n граней треугольники A 1 SA 2, A 2 SA 3,, A n SA 1 с общей вершиной S, лежащей вне плоскости основания (боковые грани). Пирамида называется правильной, если её основание правильный многоугольник, а высота пирамиды проходит через центр основания. Боковые рёбра правильной пирамиды равны, боковые грани равные равнобедренные треугольники. Двугранные углы при основании равны, двугранные углы при боковых рёбрах равны. Треугольную пирамиду называют также тетраэдром (четырёхгранником), а правильную треугольную пирамиду, все шесть рёбер которой равны, правильным тетраэдром.

6 1. Построения на проекционном чертеже (параллельная проекция) Изображение пространственной фигуры на плоскости это параллельная проекция этой фигуры на плоскость. В дальнейшем используются свойства параллельных проекций, а также следующие факты. 1. Если две различные точки прямой принадлежит плоскости, то вся прямая лежит в этой плоскости (аксиома стереометрии). 2. Если две различные плоскости имеют общую точку, то их пересечение прямая, проходящая через эту точку (аксиома стереометрии). 3. Если плоскость α проходит через прямую a, параллельную плоскости β, и пересекает эту плоскость, то прямая пересечения параллельна прямой a. 4. Если пересекающиеся плоскости α и β проходят через параллельные прямые a и b соответственно, то прямая пересечения этих плоскостей параллельна прямым a и b. 5. Прямые пересечения двух параллельных плоскостей третьей плоскостью параллельны. 6. Наклонная пересекает плоскость в точке, лежащей на любой параллельной проекции наклонной на эту плоскость. Подготовительные задачи Построение прямой пересечения двух плоскостей 1. Дана четырёхугольная призма ABCDA 1 B 1 C 1 D 1. Постройте прямую пересечения плоскостей AA 1 C 1 и BB 1 D 1 (т. е. на изображении призмы ABCDA 1 B 1 C 1 D 1 постройте изображение прямой пересечения плоскостей AA 1 C 1 и BB 1 D 1 ). 2. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Постройте прямую пересечения плоскостей BB 1 D 1 и ABC Дана треугольная призма ABCA 1 B 1 C 1, M точка пересечения медиан основания ABC. Постройте прямую пересечения плоскостей ABC и A 1 MC Четырёхугольник ABCD основание пирамиды SABCD. Постройте прямую пересечения плоскостей ASB и CSD, если: а) прямые AB и CD пересекаются; б) прямые AB и CD параллельны.

7 6 1. Построения на проекционном чертеже (параллельная проекция) 5. Основание пирамиды SABCD трапеция ABCD с основаниями AD и BC. Точка M лежит на ребре SB. Постройте прямую пересечения плоскостей ADM и SBC. 6. Дана треугольная пирамида ABCD, M точка пересечения медиан грани ABC. Постройте прямую пересечения плоскости ADC с плоскостью, проходящей через точку M параллельно прямым AC и BD. 7. Дана треугольная призма ABCA 1 B 1 C 1, M точка, лежащая на ребре CC 1. Постройте прямую пересечения плоскостей ABC и BMA Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Точки K, L и M лежат на рёбрах AD, CD и BB 1 соответственно. Постройте прямую пересечения плоскостей KLM и BB 1 D 1 D. 9. Основание пирамиды SABCDEF шестиугольник ABCDEF, противоположные стороны которого попарно равны и параллельны. Постройте прямую пересечения плоскостей ASD и CSF. 10. Дана шестиугольная призма ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, основания которой правильные шестиугольники. Точка O центр основания ABCDEF, M середина бокового ребра DD 1. Постройте прямую пересечения плоскости A 1 B 1 C 1 с плоскостью, проходящей через точки O и M параллельно прямой AE. Построение точки пересечения прямой с плоскостью Пример 1. Докажите, что в параллелепипеде ABCDA 1 B 1 C 1 D 1 диагональ AC 1 проходит через точку пересечения медиан треугольника BA 1 D и делится ею в отношении 1 : 2, считая от точки A. Р е ш е н и е. Пусть O центр параллелограмма ABCD. Тогда A 1 O медиана треугольника BA 1 D. Поскольку A 1 и O общие точки плоскостей BA 1 D и AA 1 C 1 C, эти плоскости пересекаются по прямой A 1 O. Прямые AC 1 и A 1 O, лежащие в плоскости AA 1 C 1 C, пересекаются A 1 D 1 B 1 C 1 M A B O D C

8 Подготовительные задачи 7 в некоторой точке M. Тогда M точка пересечения прямой AC 1 плоскостью BA 1 D. Из подобия треугольников AMO и C 1 MA 1 следует, что с AM = OM = OA = OA MC 1 MA 1 A 1 C 1 AC = 1 2. Точка M лежит на медиане A 1 O треугольника BA 1 D и делит эту медиану в отношении 2 : 1, считая от вершины. Следовательно, M точка пересечения медиан треугольника BA 1 D. 1. Дана треугольная пирамида ABCD. Точка M лежит на ребре BC, причём BM : MC= 1 : 2. Постройте точку пересечения прямой, проходящей через точку M и середину ребра CD, с плоскостью ABD. 2. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Точка M лежит на ребре AA 1. Постройте точку пересечения прямой DM с плоскостью A 1 B 1 C Дана треугольная призма ABCA 1 B 1 C 1, M точка пересечения медиан грани ABC, точка N лежит на боковом ребре CC 1. Постройте точку пересечения прямой MN с плоскостью A 1 B 1 C Дана четырёхугольная пирамида SABCD, основание которой параллелограмм ABCD. Точка M лежит на боковом ребре SC. Постройте точку пересечения прямой BM с плоскостью ASD. 5. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Точка M лежит на ребре AA 1. Постройте точку пересечения прямой CM с плоскостью A 1 B 1 C Дана треугольная пирамида ABCD, M точка пересечения медиан грани ABC. Постройте точку пересечения прямой, проходящей через точку B и середину отрезка DM, с плоскостью ACD. 7. Дана треугольная пирамида ABCD. Точки K, L и M лежат на рёбрах AB, BC и CD соответственно. Постройте точку пересечения прямой KM с плоскостью ALD. 8. Дана четырёхугольная пирамида SABCD с вершиной S. Точка M лежит на боковом ребре SD. Постройте точку пересечения прямой BM с плоскостью ASC. 9. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Точка M лежит на ребре DD 1. Постройте точку пересечения прямой DB 1 с плоскостью AMC. 10. Основание пирамиды SABCDEF шестиугольник ABCDEF, противоположные стороны BC и EF которого параллельны. Точка M лежит на ребре SC. Постройте точку пересечения прямой BM с плоскостью ESF.

9 8 1. Построения на проекционном чертеже (параллельная проекция) Построение сечений многогранников 1. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: а) B, D и середину M ребра AC; б) B и середины рёбер AD и CD; в) середину K ребра AD и точки L и M, лежащие на продолжениях рёбер AB и AC за точки B и C; г) середины рёбер BC, AD и точку L, лежащую на продолжении ребра AC за точку C; д) середины K, L и M рёбер AD, AB и BC; е) A, C и точку пересечения медиан грани ABD; ж) середины рёбер AD, CD и точку M, лежащую на ребре BC, если BL : LC= 1 : 2; з) K, L и M, лежащие на рёбрах AD, AB и BC соответственно, если AK : KD=BL : LA= BM : MC= 1 : 2; и) точки пересечения медиан граней ABD, BCD и ABC; к) середины рёбер BC, CD и точку, лежащую на медиане DM грани ABD. 2. Постройте сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через следующие точки: а) середины рёбер AB, AD и AA 1 ; б) B, C и середину ребра A 1 B 1 ; в) A, C и середину ребра A 1 B 1 ; г) середины рёбер AA 1, AD и центр грани BB 1 C 1 C; д) центры граней ABCD, AA 1 B 1 B и BB 1 C 1 C; е) середины рёбер AB, BC и DD 1 ; ж) середины рёбер A 1 B 1, CC 1 и вершину A; з) середину ребра CC 1 и точки K, L, лежащие на рёбрах AB и A 1 B 1, если BK : KA= A 1 L : LB 1 = 1 : 2; и) середину ребра A 1 B 1, вершину A и точку M на ребре B 1 C 1, если B 1 M : MC 1 = 1 : 3; к) середины рёбер AD, CD и A 1 B 1 ; л) середины рёбер AB, BC и CC 1 ; м) вершину B 1, центр грани ABCD и середину ребра AA 1 ; н) середины рёбер CD, BC и точку M, лежащую на продолжении ребра AA 1 за точку A 1, если MA 1 = 1 2 AA 1; о)* середины рёбер AD, CC 1 и A 1 B Постройте сечение треугольной призмы ABCA 1 B 1 C 1 плоскостью, проходящей через следующие точки:

10 Подготовительные задачи 9 а) середину ребра AA 1 и вершины B и C 1 ; б) середины рёбер AA 1, B 1 C 1 и вершину B; в) центры граней AA 1 B 1 B, BB 1 C 1 C и точку M ребра BC, если CM : MB=1:2; г) середины рёбер AB, A 1 C 1 и CC 1 ; д) середины рёбер AA 1, A 1 C 1 и центр основания ABC; е) центр грани AA 1 B 1 B, середину ребра B 1 C 1 и точку M ребра A 1 C 1, если A 1 M : MC 1 = 1 : 2. ж) центр основания ABC и центры боковых граней AA 1 B 1 B и BB 1 C 1 C. 4. Основание пирамиды SABCD параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: а) A, B и середина ребра SD; б) середины рёбер AB, BC и SC; в) середины рёбер AB, BC и SD; г) середины рёбер AB, AD параллельно ребру SC; д) середины рёбер AD, SC и точку B; е) середины рёбер AB, AD и SC; ж) центр основания, середину ребра SD и точку M ребра SA, если AM : MS= 1 : 3; з) середину ребра SA и точки M и N рёбер SB и SC, если BM : MS= = SN : NC= 1 : Основание шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: а) A, B и F 1 ; б) A, C и D 1 ; в) B, E и середину ребра FF 1 ; г) B, D и середину ребра AA 1 ; д) B, C и E 1 ; е) B, C и середину ребра DD 1 ж) B, D и середину ребра FF Основание шестиугольной пирамиды SABCDEF правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: а) C, F и середину ребра SD; б) A, B и середину ребра SD; в) центр основания параллельно плоскости ASB; г) A, C и середину ребра SD;

11 10 1. Построения на проекционном чертеже (параллельная проекция) д) B и середины рёбер AS и CS; е) B, C и середину отрезка, соединяющего вершину пирамиды с центром основания. Задачи на построение на проекционном чертеже и вычисление отношений отрезков 1.1. Точка M лежит на ребре AB треугольной пирамиды ABCD, причём AM : MB=1:2. точку M и середины рёбер BC и AD. б) В каком отношении плоскость сечения делит ребро CD? 1.2. Точка M середина ребра AD треугольной пирамиды ABCD. Точки K и L лежат на прямых AB и AC соответственно, причём B середина отрезка AK, а C середина отрезка AL. точки M, K и L. б) В каком отношении плоскость сечения делит ребро BD? 1.3. Точки M и N середины рёбер соответственно AB и BC параллелепипеда ABCDA 1 B 1 C 1 D 1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки M, N и D 1. б) В каком отношении плоскость сечения делит ребро AA 1? 1.4. Точка M середина ребра CD параллелепипеда ABCDA 1 B 1 C 1 D 1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки M, A 1 и C 1. б) Пусть секущая плоскость пересекает прямую DD 1 в точке P. Найдите отношение PD : PD Основание пирамиды SABCD параллелограмм ABCD с центром O. Точка M лежит на отрезке SO, причём OM : MS= 1 : 2. прямую AM параллельно прямой BD. б) В каком отношении плоскость сечения делит ребро SC? 1.6. Основание пирамиды SABCD параллелограмм ABCD с центром O. Точка M середина отрезка AO. точку M параллельно прямым SA и BD. б) В каком отношении плоскость сечения делит ребро SC? 1.7. Точки M и N середины рёбер соответственно CC 1 и AB треугольной призмы ABCA 1 B 1 C 1.

12 Задачи на построение на чертеже 11 а) Постройте сечение призмы плоскостью, проходящей через точки M, N и A 1. б) В каком отношении плоскость сечения делит ребро BC? 1.8. Точки M и N середины рёбер соответственно AA 1 и AB треугольной призмы ABCA 1 B 1 C 1. а) Постройте сечение призмы плоскостью, проходящей через точки M, N и C 1. б) В каком отношении плоскость сечения делит ребро BC? 1.9. Основания шестиугольной призмы ABCDEFA 1 B 1 C 1 E 1 F 1 правильные шестиугольники. Точка M середина ребра AA 1. а) Постройте сечение призмы плоскостью, проходящей через точки C, D и M. б) В каком отношении плоскость сечения делит ребро BB 1? Основания шестиугольной призмы ABCDEFA 1 B 1 C 1 E 1 F 1 правильные шестиугольники. а) Постройте сечение призмы плоскостью, проходящей через точки A, B и D 1. б) В каком отношении плоскость сечения делит ребро FF 1? Основание шестиугольной пирамиды SABCDEF правильный шестиугольник ABCDEF. Точки M и N середины рёбер BC и EF. прямую MN параллельно ребру SA. б) В каком отношении плоскость сечения делит ребро SC? Основание шестиугольной пирамиды SABCDEF правильный шестиугольник ABCDEF. прямую BF параллельно ребру SA. б) В каком отношении плоскость сечения делит ребро SC? Точка M середина ребра AD параллелепипеда ABCDA 1 B 1 C 1 D 1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точку M параллельно прямым BD и CB 1. б) В каком отношении плоскость сечения делит диагональ AC 1 параллелепипеда? Точка M середина ребра AD параллелепипеда ABCDA 1 B 1 C 1 D 1. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки M и B 1 параллельно прямой A 1 C 1. б) В каком отношении плоскость сечения делит диагональ BD 1 параллелепипеда?

13 12 1. Построения на проекционном чертеже (параллельная проекция) Точки M и N середины рёбер соответственно AB и CD треугольной пирамиды ABCD. точку пересечения медиан треугольника ABC параллельно прямым AB и CD. б) В каком отношении плоскость сечения делит отрезок MN? Точки M и N середины рёбер соответственно AB и CD треугольной пирамиды DABC. середину ребра AD параллельно прямым AB и CD. б) В каком отношении плоскость сечения делит отрезок MN? Дана четырёхугольная пирамида SABCD, основание которой параллелограмм ABCD. Точка M середина ребра AB. точку M параллельно прямым AC и SB. б) В каком отношении плоскость сечения делит отрезок, соединяющий точку D с серединой ребра SB? Дана четырёхугольная пирамида SABCD, основание которой параллелограмм ABCD. Точка M середина ребра SD. прямую BM параллельно прямой AC. б) В каком отношении плоскость сечения делит отрезок, соединяющий точку S с центром параллелограмма ABCD? Точка M середина ребра AB треугольной призмы ABCA 1 B 1 C 1. а) Постройте сечение призмы плоскостью, проходящей через прямую A 1 M параллельно прямой AC. б) В каком отношении плоскость сечения делит отрезок, соединяющий точку B 1 с серединой ребра AC? Точки M и N середины рёбер соответственно AC и BB 1 треугольной призмы ABCA 1 B 1 C 1. а) Постройте прямую пересечения плоскостей MNC 1 и A 1 B 1 C 1. б) В каком отношении плоскость MNC 1 делит ребро AB? Основания шестиугольной призмы ABCDEFA 1 B 1 C 1 E 1 F 1 правильные шестиугольники. Точка M середина ребра CC 1, O центр грани ABCDEF. а) Постройте сечение призмы плоскостью, проходящей через точки M, O и E 1. б) В каком отношении плоскость сечения делит ребро EF?

14 Задачи на построение на чертеже Основания шестиугольной призмы ABCDEFA 1 B 1 C 1 E 1 F 1 правильные шестиугольники. Точка M середина ребра CC 1. а) Постройте прямую пересечения плоскостей D 1 ME 1 и ABC. б) В каком отношении плоскость D 1 ME 1 делит диагональ B 1 E призмы? Основание шестиугольной пирамиды SABCDEF правильный шестиугольник ABCDEF. Точки M и N середины рёбер SA и SC. точки M, N и B. б) В каком отношении плоскость сечения делит отрезок, соединяющий вершину S с центром основания пирамиды? Основание шестиугольной пирамиды SABCDEF правильный шестиугольник ABCDEF. Точка M середина ребра BC. а) Постройте прямую пересечения плоскостей FSM и ASB. б) В каком отношении плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD?

15 Содержание Предисловие Краткий список основных сведений о многогранниках Построения на проекционном чертеже (параллельная проекция) Угол между прямыми Угол между плоскостями Расстояние от точки до прямой. Расстояние от точки до плоскости Угол между прямой и плоскостью Расстояние между скрещивающимися прямыми Площадь сечения Объём многогранника Фигуры вращения Элементы правильных пирамид Приложение. Метод координат Диагностические работы Диагностическая работа Диагностическая работа Диагностическая работа Диагностическая работа Диагностическая работа Диагностическая работа Ответы

Видео:Построение сечения пирамиды по трем точкамСкачать

Пересечения двух произвольно заданных плоскостей

Решение задачи в соответствии с выставленными принципами, понимание которых учащимся к этому моменту должно быть.подготовлено, не должно уже вызывать затруднений В одной из заданных плоскостей (рис.5), например в плоскости φ(φ1), берутся две произвольные вспомогательные прямые а(а) и в(в) и строятся точки — точки Х(Х1) и Y(Y1) — пересечения этих прямых с плоскостью β(β1). Прямая XY(X1Y1)— искомая.

В повседневной практике в качестве вспомогательных прямых выбирают те, которые имеются уже на чертеже: следы плоскостей, прямые, определяемые точками, задающими плоскость. Одна точка линии пересечения плоскостей, заданных на рис. 6, определяется как точка пересечения следов плоскостей — точка Х(Х1). В качестве второй вспомогательной прямой а(а,) взята прямая, лежащая в проектирующей плоскости РP1 ТT1.

Для закрепления решения этой задачи можно предложить следующую систему задач:

Плоскость задана тремя точками, расположенными на смежных боковых ребрах пирамиды (призмы). Найти линию пересечения этой плоскости с плоскостью нижнего основания.

Плоскость задана тремя точками, расположенными на не смежных боковых ребрах пирамиды, в основании которой лежит четырехугольник. Найти линию пересечения этой плоскости с плоскостью нижнего основания.

Плоскость задана тремя точками, две из них расположены на смежных боковых ребрах пирамиды, а третья – на боковой грани пирамиды. Найти линию пересечения этой плоскости с плоскостью нижнего основания.

Дана четырехугольная пирамида SABCD. Построить линию пересечения двух ее граней ASB и CSD

Дана четырехугольная призма ABCDABCD. Найти линию пересечения плоскости, заданной точками В,К,L, где В-вершина основания, точка K принадлежит ребру DD1,точка L принадлежит ребру CC1,с плоскостью A1B1C1D1.

Точки О и О1 являются точками пересечения диагоналей оснований куба. Найти линии пересечения плоскости, заданной точками О, О1,С с боковыми гранями.

Дано SABCD — пирамида. Точка Н- середина DC. Найти линию пересечения плоскости, заданной точками A,H,S,с плоскостью SBC.

Но для полноценного решения задач на построении полезно на основании двух опорных задач (нахождении точки пересечения с плоскостью и линии пересечения плоскостей) рассмотреть задачи.

Задача 1. Найти точку пересечения плоскости Q, заданной следом ВС и точкой А(А1), с проектирующей прямой DD1 (рис. 7а).

Проводим плоскость R через точку А(А1) и данную прямую DD1 и на линии AM пересечения плоскостей Q и R находим искомую точку Х(Х1).

Информация по теме:

Причины и следствия отклоняющегося поведения младших школьников
Отклоняющимся обычно называют поведение школьников, вызванное неспецифическими (т. е. не врожденными) факторами. Сюда относятся обычные детские шалости, нарушения дисциплины, иногда хулиганские поступки, свойственные детскому возрасту. Они чаще всего обусловлены ситуацией и детской готовностью их с .

Система уроков по изучению рассказа Л.Н. Толстого «Кавказский пленник»
Часть 1. Знакомство с героями Эпизод 1. Письмо от матери. Социальное положение героев, отношение Жилина к матери. Эпизод 2. Отпуск. Щедрость Жилина, его отношения с товарищами. Эпизод 3. В дороге. Решение Жилина ехать одному. Появление второго героя, его портрет. Эпизод 4. Встреча с татарами. Как в .

Диагностика определяющей рефлексии
Диагностика, которая проводилась в пятом классе, является пробной, так как мы воспользовались диагностикой определяющей рефлексии по отношению к себе для 1-3 классов, но изменили и усложнили задания и вопросы в соответствии с возрастом. Набор задач для 5 класса представлен в приложении 1. В работе .

📹 Видео

Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать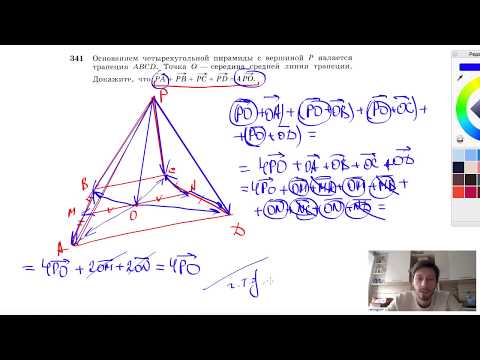

Построение сечений (часть 1). Пирамиды. сечениеСкачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Построение проекций пирамиды. Анимация.Скачать

Начертательная геометрияСкачать

Задача 3.5. Построить проекции ромба ABCD, если вершина А равноудалена от П1 и П2, диагональ АС//П1Скачать

№243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать

№29. В трапеции ABCD основание ВС равно 12 см. Точка М не лежит в плоскостиСкачать

Построение точек встречи прямой m с поверхностью сферыСкачать

№517. Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 смСкачать

№19. Стороны АВ и ВС параллелограмма ABCD пересекают плоскость αСкачать

№30. Основание АВ трапеции ABCD параллельно плоскости α, а вершина С лежитСкачать

№70. Докажите, что плоскость, проходящая через середины ребер АВ, АС и AD тетраэдра ABCD,Скачать

№174. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и ACB прямые, ACСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать