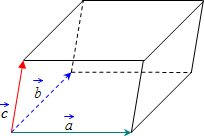
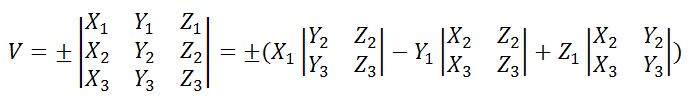Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Объём параллелепипеда
Объём параллелепипеда, построенного на трех векторах
где координаты векторов в соответствии с рисунком
вычисляются следующим образом
Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.
Найти объём параллелепипеда, построенного на векторах a1=, a2= и a3=
$ = pm left( <2cdotleft( <left( right)cdot2 — 1cdot3> right) — 3left( <left( right)cdot2 — 3cdot3> right) + 2left( <left( right)cdot1 — 3cdotleft( right)> right)> right) = -33$
Так как определитель отрицателен, берем перед ним знак « − ».
Тогда объём параллелепипеда построенного на векторах равен V=33
Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Ориентированные площади и объёмы
Видео:§20 Нахождение объёма параллелипипедаСкачать

Ориентированная площадь параллелограмма
Ориентированной площадью параллелограмма , построенного на неколлинеарных векторах и , называется его площадь , взятая со знаком плюс, если ориентация пары векторов и правая , и со знаком минус, если ориентация — левая
Внешним (косым) произведением неколлинеарных векторов и на плоскости называется число, равное ориентированной площади параллелограмма, построенного на этих векторах. Если векторы и коллинеарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается . Его свойства повторяют алгебраические свойства векторного произведения, т.е. для любых векторов на плоскости и любого числа справедливы равенства:
4) Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то внешнее произведение этих векторов находится по формуле
Если — координатные столбцы векторов в стандартном базисе на плоскости, то их внешнее произведение находится по формуле
Приведенные свойства внешнего произведения следуют из алгебраических свойств векторного произведения, если векторы на плоскости рассматривать как векторы в пространстве с нулевыми аппликатами.
Рассмотрим задачу разложения вектора по базису на плоскости. Отложим все векторы от произвольной точки . Сначала разберем случаи, когда векторы и коллинеарны: одинаково направлены (рис.1.49,а) или противоположно направлены (рис. 1.49,6). В этих случаях ордината вектора равна нулю, а абсцисса находится как отношение
так как пара в первом случае правая (рис.1.49,а), а во втором случае — левая (рис.1.49,б).
Пусть теперь векторы и не коллинеарны (рис.1.49,в). Построим проекции и на прямые, содержащие базисные векторы: . Из концов векторов и опустим перпендикуляры и соответственно на прямую, содержащую вектор . Учитывая, что векторы и противоположно направлены, а также подобие прямоугольных треугольников с гипотенузами и , находим абсциссу вектора :
так как пара — правая, а пара — левая. Аналогично находится ордината (векторы и одинаково направлены)
Таким образом, вектор имеет следующее разложение по базису на плоскости:
Рассмотрим применение формулы (1.19) для решения системы двух линейных уравнений с двумя неизвестными:
Эту систему можно записать в виде .Рассматривая полученные столбцы как координатные столбцы векторов в стандартном базисе на плоскости, получаем разложение .
Таким образом, нахождение решения системы уравнений свелось к задаче разложения вектора по векторам и . Предполагая, что коэффициенты при неизвестных не пропорциональны, т.е. (векторы и не коллинеарны), по формуле (1.19), полагая , получаем:
Видео:Решение, вычислите объем параллелепипеда, построенного на векторах a, b, c пример 4Скачать

Ориентированный объем параллелепипеда
Ориентированным объемом параллелепипеда , построенного на некомпланарных векторах , называется его объем , взятый со знаком плюс, если ориентация тройки векторов правая и со знаком минус, если ориентация — левая .
Внешним (косым) произведением некомпланарных векторов называется число, равное ориентированному объему параллелепипеда, построенного на этих векторах. Если векторы компланарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается .
Внешнее произведение трех векторов совпадает с их смешанным произведением (в силу первого геометрического свойства смешанного произведения), т.е. . В ортонормированием базисе
так как определитель транспонированной матрицы равен определителю исходной матрицы.
При помощи ориентированных объемов задача разложения вектора по базису в пространстве решается так же как и на плоскости с использованием ориентированных площадей. В результате получаем
Формула (1.21) соответствует правилу Крамера решения системы трех линейных уравнений с тремя неизвестными.
Пример 1.23. Заданы координатные столбцы
векторов в стандартном базисе. Разложить вектор по векторам .
Решение. По формуле (1.20) находим смешанные произведения
Коэффициенты разложения определяем по формуле (1.21):
🔥 Видео
Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Площадь параллелограмма по векторамСкачать

Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать
как найти площадь параллелограмма построенного на векторахСкачать

Решение, найти высоту параллелепипеда, построенного на векторах a, b, c пример 17 Высшая математикаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Решение, вычислить объем параллелепипеда, построенного на векторах a, b, c пример 11Скачать

Решение, найдите объем параллелепипеда, построенной на векторах a, b, c пример 7. Высшая математикаСкачать

Площадь треугольника, построенного на векторахСкачать

Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

Решение, вычислить высоту параллелепипеда, построенного на векторах a, b, c пример 16Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Нахождение объема параллелепипеда, построенного на векторах а, b и с. пример 2Скачать

Решение, найти высоту параллелепипеда, построенного на векторах a, b, c пример 18 Высшая математикаСкачать

1. Векторы и параллелограмм задачи №1Скачать

Правило параллелепипеда для векторовСкачать