Через точку м провести прямую общего положения параллельную плоскости авс

Построение прямой, параллельной заданной плоскости, основано на следующем положении, известном из геометрии: прямая параллельна плоскости, если эта прямая параллельна любой прямой в плоскости.

Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие.

Например, через точку М (рисунок 140) требуется провести прямую, параллельную плоскости, заданной треугольником ЛВС, и плоскости проекций тс! (дополнительное условие).

Очевидно, искомая прямая должна быть параллельна линии пересечения обеих плоскостей, т. е. должна быть параллельна горизонтальному следу плоскости, заданной треугольником АВС. Для определения направления этого следа можно воспользоваться горизонталью плоскости, заданной треугольником АВС. На рисунке 140 проведена горизонталь DC и затем через точку М проведена прямая, параллельная этой горизонтали.

Поставим обратную задачу: например, надо провести плоскость, параллельную прямой CD, через прямую АВ (рисунок 141).

Прямые АВ и CD — скрещивающиеся. Если через одну из двух скрещивающихся прямых требуется провести плоскость, параллельную другой, то задача имеет единственное решение. Через точку В проведена прямая, параллельная прямой CD; прямые АВ и BE определяют плоскость, параллельную прямой CD.

Как установить, параллельна ли данная прямая данной плоскости? Можно попытаться провести в этой плоскости некоторую прямую параллельно данной прямой. Если такую прямую в плоскости не удается построить, то заданные прямая и плоскость не параллельны между собой.

Можно попытаться найти также точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.

Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Признаки параллельности прямой и плоскости

Признаки параллельности прямой и плоскости имеют следующее определение — прямая m параллельна плоскости α, если в плоскости α можно провести прямую n, параллельную m:

Очевидно через точку пространства, не принадлежащую плоскости, можно провести бесчисленное множество прямых, параллельных данной плоскости.

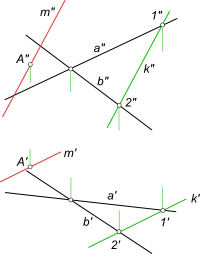
Через точку A провести прямую m, параллельную плоскости α, заданной пересекающимися прямыми a и b

Если нет никаких дополнительных условий, то мы вправе, используя признаки параллельности прямой и плоскости, провести любую прямую из множества прямых, проходящих через точку A и параллельных плоскости α — например параллельно одной из прямых a или b. Если же поставлено условие, чтобы прямая не была параллельна прямым a и b — необходимо построить прямую 12 и провести искомую прямую m(m`, m») параллельно ей.

Через заданную точку A провести плоскость, параллельную прямой f

Плоскость задаем пересекающимися в точке A прямыми a и b. При этом одна из прямых (прямая a) параллельна прямой f.

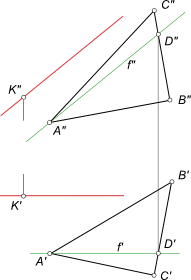
Через заданную точку K провести прямую, параллельную плоскости треугольника ABC и фронтали, проходящей через вершину A

Построим фронталь f по заданному условию: — через точку A` параллельно оси x проводим прямую f`. Данная прямая пересекает B`C` — сторону треугольника в точке D`. По линии связи находим фронтальную проекцию D» точки D, принадлежащей стороне BC треугольника. Проводим через точки A» и D» прямую f». Через точку K проводим прямую параллельную фронтали f. Данная прямая будет параллельна и плоскости треугольника ABC.

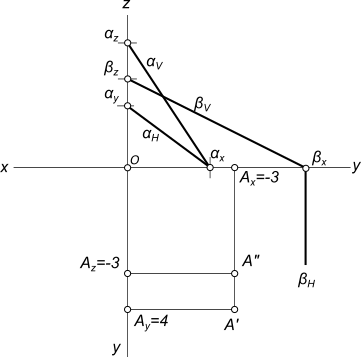
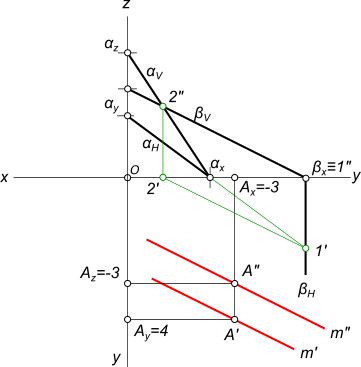
Через точку A(-3;4;-3) провести прямую параллельную двум плоскостям α(3x+4y-2z+7=0) и β(x-2z+5=0)

1. Строим проекции точки A 2. Строим следы плоскости α (3x+4y-2z+7=0): a) z=0; 3x+4y+7=0; αH; y=0; 3x+7=0, x=-7/3, x=-2,33; b) y=0; 3x-2z+7=0; αV; x=0; -2z+7=0, z=3,5; z=0; 3x+7=0, x=-2,33 3) Строим следы плоскости β (x-2z+5=0): βV x=0; -2z+5=0, z=5/2, z=2,5; z=0; x+5=0, x=-5 4) Строим линию пересечения 1—2 заданных плоскостей α и β

5) Строим линию m параллельную плоскостям α и β: m`‖1`—2` и m»‖1″—2″

Видео:Параллельность прямой к плоскостиСкачать

Лекция 3. Плоскость

Видео:Проецирование прямой общего положенияСкачать

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

Видео:Точка встречи прямой с плоскостьюСкачать

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

Видео:Проецирование плоскости общего положенияСкачать

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

left.beginalpha=mparallel n,\Dinalpha\Cinalpha\endright> Longrightarrow CDinalpha

Видео:Задача 3.3. Через точку М провести горизонталь и фронталь.Скачать

Упражнение

Рисунок 3.7 – Решение задачи

Решение :

1. ABCD – плоский четырехугольник, задающий плоскость.
2. Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
3. Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A₂C₂ ∩ B₂D₂=K₂.
4. Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B₁D₁ строим К₁.
5. Через А₁К₁ проводим проекцию диагонали А₁С₁.
6. Точку С₁ получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А₁К₁.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

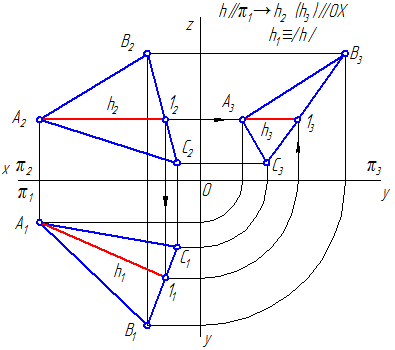
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

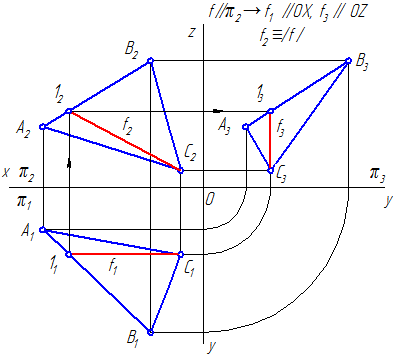
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Интерактивная модель Горизонталь плоскости

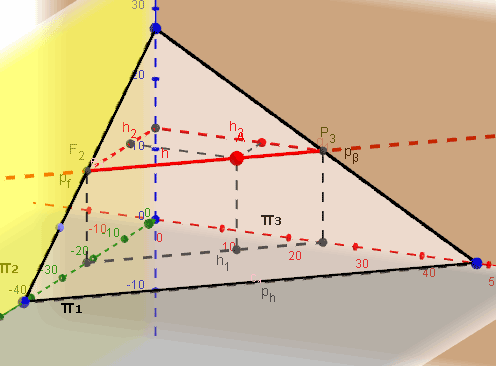Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Интерактивная модель Фронталь плоскости

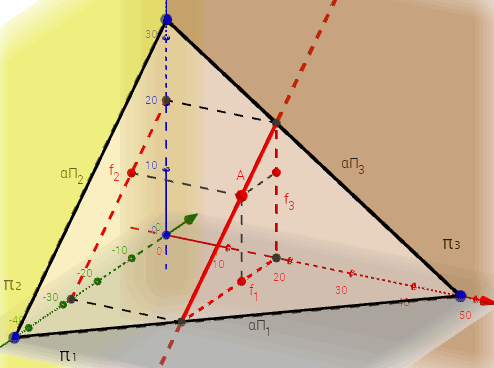Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Интерактивная модель Профильная прямая плоскости

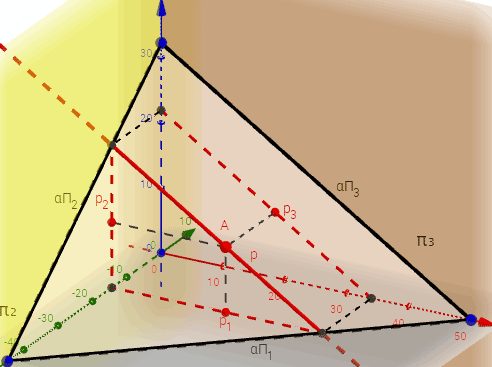Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

Видео:Провести горизонтальную прямую через точку и пересекающую заданный отрезок. Начертательная геометрияСкачать

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

alpha=mcap n\left.begina_2parallel m_2\a_1parallel m_1\endright> Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

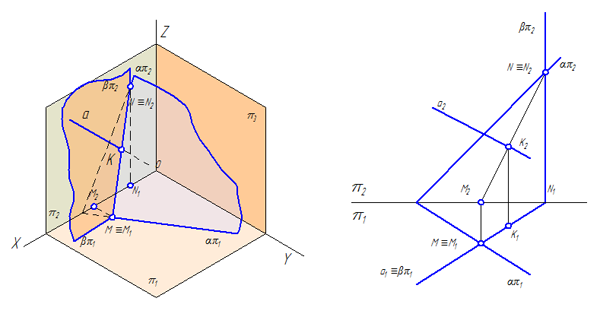
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

1. Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
2. Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
3. Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Видео:Линия пересечения плоскостейСкачать

Упражнение

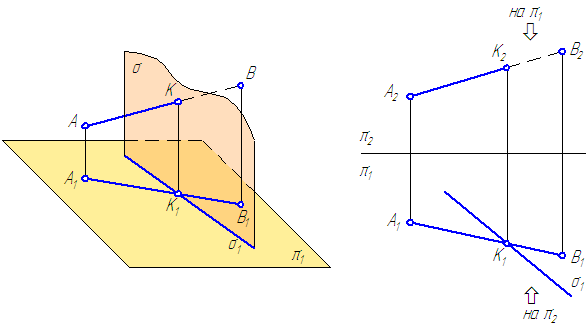
Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

1. 1. Точка К должна принадлежать прямой АВ ⇒ К₁∈А₁В и заданной плоскости σ ⇒ К₁∈σ, следовательно, К₁ находится в точке пересечения проекций А₁В₁ и σ₁;
   2. Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ₁ (горизонтальный след плоскости);
   3. Фронтальную проекцию точки К находим посредством линии проекционной связи: К₂∈А₂В₂.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

Решение:

1. Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
2. Если α⊥π₁, то на плоскость проекций π₁ плоскость α проецируется в прямую (горизонтальный след плоскости απ₁ или α₁), совпадающую с E₁F₁;
3. Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
4. Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.

Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:

1. left.beginalpha perp pi_1\alphain EF\endright> Longrightarrow alpha_1in E_1F_1
2. alphacapsigma=(1-2)left.begin|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\endright.
3. (1_2-2_2)cap E_2F_2=K_2\left.beginKin EF\Kin (1-2)Rightarrow Kinsigma\endright>Longrightarrow K=EFcap (sigma =triangle ABC)

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

Видео:Через точку К, сим-ную точке D относительно пл-ти α(АВС), построить плоскость, парал. плоскости α.Скачать

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Видео:Угол наклона плоскости общего положения относительно плоскостям проекцииСкачать

Упражнение

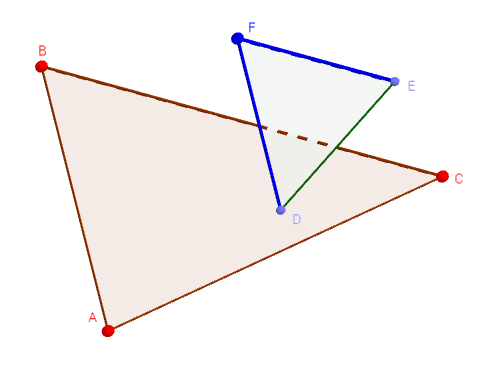
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение : В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

1. Через точку F проводим прямую m, параллельную, например, АВ.
2. Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
3. β = m∩n и β//α по определению.

Интерактивная модель Параллельность двух плоскостей

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей:

1. Найти точку пересечения горизонтальных следов — это точка М (её проекции М₁ и М₂, при этом М₁=М, т.к. М – точка частного положения, принадлежащая плоскости π₁).
2. Найти точку пересечения фронтальных следов — это точка N (её проекции N₁ и N₂, при этом N₂=N, т.к. N – точка частного положения, принадлежащая плоскости π₂).
3. Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М₁N₁ и М₂N₂.

МN – линия пересечения плоскостей.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Упражнение

Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K₁ и L₁ , на пересечении горизонтального следа (α₁) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А₁В₁ и A₁C₁. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K₂ и L₂ на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K₁ и L₁; K₂ и L₂. Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

left.beginABcapsigma=K\ACcapsigma=L\endright> left.beginRightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\endright.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать

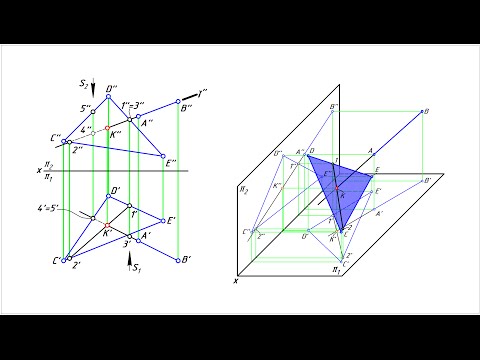
Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

left.beginalphacapsigma=(4-5)\betacapsigma=(3-2)\endright>\left.beginalphacaptau=(6-7)\betacaptau=(1-8)\endright>left.begin(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\endright>rightarrow\left.beginM_1N_1\M_2N_2\endright>Rightarrowalphacapbeta=MN

Видео:Строим фронталь и горизонталь в плоскости общего положения удаленную от П1 П2 на какое то расстояниеСкачать

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

Видео:Пересечение прямой и плоскостиСкачать

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Видео:Следы плоскости общего положения заданной фронталью и горизонталью. Начертательная геометрия легкоСкачать

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.