Тест 21 четыре замечательные точки окружности вариант (3 видео)

Тест по геометрии на тему » Четыре замечательные точки» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Содержание

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Описание презентации по отдельным слайдам:
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
Сборник тестов по геометрии 8 класс
Просмотр содержимого документа «Сборник тестов по геометрии 8 класс»
ГДЗ по геометрии 8 класс Гаврилова контрольно-измерительные материалы
📸 Видео

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тест : Четыре замечательные точки треугольника

1 . Серединный перпендикуляр — это прямая, проходящая через …….(продолжить)

2. Любая точка, лежащая на серединном перпендикуляре к отрезку, .

1) равноудалена от концов отрезка.
2) равноудалена от всех точек отрезка.
3) равноудалена от прямых, проходящих через концы отрезка.

3. Сколько всего можно провести серединных перпендикуляров в треугольнике:

4. Где находится центр вписанной окружности в треугольник

1) в точке пересечения биссектрис
2) в точке пересечения серединных перпендикуляров
3) в точке пересечения высот

5. Если точка лежит на биссектрисе угла, то .
1) она лежит на перпендикуляре к сторонам угла.
2) ни один вариант ответа не является верным.
3) она равноудалена от сторон угла

6. Сколько всего можно провести биссектрис в треугольнике:

7. Где находится центр описанной окружности около треугольника

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 679 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 302 человека из 66 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 507 556 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 3. Четыре замечательные точки треугольника

Другие материалы

14.07.2021
81
2

13.07.2021
43
1

13.07.2021
46
1

13.07.2021
47
1

13.07.2021
138
16

13.07.2021
105
1

13.07.2021
90
1

13.07.2021
91
0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

14.07.2021 79
PPTX 55.8 кбайт
2 скачивания
Оцените материал:

Настоящий материал опубликован пользователем Кучумова Ирина Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 4 года и 5 месяцев
Подписчики: 0
Всего просмотров: 4560
Всего материалов: 15

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Четыре замечательные точки треугольника. Видеоурок 20. Геометрия 8 классСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

Минобрнауки запускает конкурс студенческих научных обществ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Четыре замечательные точки треугольникаСкачать

Сборник тестов по геометрии 8 класс

В данном сборнике предлагается система тестов для контроля качества усвоения теоретического материала по геометрии для учащихся 8 класса. Тематика и содержание тестов соответствуют требованиям программы по геометрии для 8 класса. Предлагаемый сборник обеспечивает всестороннее повторение материала в течение учебного года. Задания тестов ориентированы на определение уровня усвоения ключевых понятий, тем и разделов учебной программы.

Просмотр содержимого документа
«Сборник тестов по геометрии 8 класс»

Пояснительная записка
В данном сборнике предлагаются тематические тесты для контроля качества усвоения теоретического материала по геометрии для учащихся 8 класса. Тематика и содержание тестов соответствуют требованиям программы по геометрии для учащихся 8 класса.
Задания тестов ориентированы на определение уровня усвоения ключевых понятий, тем и разделов учебной программы. Они внесут разнообразие в контроль и коррекцию знаний, умений и навыков и не отнимут много времени. И в то же время анализ выполнения тестов поможет выделить повторяющиеся ошибки как индивидуально у каждого ученика, так и в целом по классу. Тесты содержат два варианта, состоящих из трёх уровней:

Уровень А является базовым(4 задания), это задания с выбором одного правильного ответа из четырёх предложенных.

Уровень В — более сложный (2задания)-задания, ответ для которых учащиеся должны получить сами.

Уровень С включает задания повышенной сложности (1 задание), требующее подробного решения задачи.

Критерии оценки ответов.

За каждое верно выполненное задание части А начисляется 1 балл, в части В — 2 балла, в части С — 3 балла.

Примерное соответствие количества баллов и отметки.

80—100% от максимальной суммы баллов — оценка «5»;

Цель использования: Выявить степень овладения учащимися учебной программы по предмету.

Развитие интереса к предмету геометрии, повышения познавательной активности и познавательных возможностей учащихся

Этапы обучения, на которых рекомендовано использование данного сборника: актуализации знаний, закрепления изученного, повторения.

Название сборника: «Сборник тестов по геометрии 8 класс »

Автор: Дроздова Нина Ивановна, учитель математики

1.Пояснительная записка 1

2.Тест №1 «Параллелограмм» 3-4

3.Тест№2 «Прямоугольник.Ромб.Квадрат» 5-6

4.Тест№3 «Средняя линия треугольника и трапеции. Теорема Фалеса.Теорема о пропорциональных отрезках» 7-8

5.Тест№4 «Трапеция» 9-10

6.Тест№5 «Четыре замечательные точки треугольника» 11

7.Тест№6 -Теоретический тест по теме «Четырёхугольники» 12-15

8.Тест №7 «Соотношения между сторонами и углами прямоугольного треугольника» 16-19

9.Тест№8 «Теорема Пифагора» 20-21

10.Тест№9 «Декартовы координаты на плоскости» 22-23

11.Тест№10 «Площадь прямоугольника» 24-25

12.Тест№11 «Площадь параллелограмма, ромба, треугольника» 26-27

13.Тест№12 «Площадь трапеции»28-29

14.Тест№13 Теоретический тест по теме «Площадь» 30-31

15.Тест№14 Обобщающий тест по теме «Площадь» 32-35

16.Тест№15 Итоговый тест за курс 8 класса 36-37

А1. Периметр параллелограмма равен 24 см, а одна из сторон в два раза больше другой. Чему равна наименьшая из его сторон?

1) 4 см 2) 12 см 3) 9 см 4) 6 см

А2. Если в параллелограмме ABCD угол А + угол В + угол D = 272 ° , то чему равен угол А?

1) 80 ° 2) 72 ° 3) 56 ° 4) 92 °

А3. В параллелограмме ABCD диагональ АС со сторонами АВ и ВС образует углы, равные соответственно 40 ° и 35 ° . Чему равна величина угла С?

1) 25 ° 2) 105 ° 3) 70 ° 4) 110 °

А4. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 9 см, КС = 3 см. Чему равен периметр параллелограмма?

1) 24 см 2) 42 см 3) 34 см 4) 38 см

В1. В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует с диагональю BD угол 30 ° , АВ = 10 см. Найдите периметр параллелограмма.

В2. В параллелограмме ABCD биссектрисы углов B и D пересекают стороны AD и ВС в точках М и Е соответственно так, что MD = 5 см, ЕС = 7 см. Найдите периметр ABCD.

С1. На сторонах ВС и CD параллелограмма ABCD отмечены точки Р и Н соответственно так, что отрезки ВН и РD пересекаются в точке О; угол BHD = 95 ° , угол DРC = 90 ° , угол BOD = 155 ° . Найдите углы параллелограмма.

Ответ: угол С = угол А = 30 ° , угол В = угол D = 150 ° .

А1. Периметр параллелограмма равен 40 см, а две из его сторон относятся как 3 : 1. Чему равна наибольшая из его сторон?

1) 15 см 2) 10 см 3) 6 см 4) 4 см

А2. Если в параллелограмме ABCD угол А + угол В + угол С = 221 ° , то чему равен угол В?

1) 57 ° 2) 79 ° 3) 139 ° 4) 90 °

А3. В параллелограмме ABCD диагональ BD со сторонами АВ и AD образует углы, равные соответственно 54 ° и 22 ° . Чему равна величина угла В?

1) 54 ° 2) 26 ° 3) 102 ° 4) 76 °

А4. В параллелограмме ABCD биссектриса угла В пересекает сторону AD в точке М так, что АМ = 6 см, MD = 4 см. Чему равен периметр параллелограмма?

1) 40 см 2) 24 см 3) 32 см 4) 36 см

В1. В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует со стороной ВС угол 30 ° , АВ = 12 см. Найдите периметр параллелограмма.

В2. В параллелограмме ABCD биссектрисы углов А и С пересекают стороны ВС и AD в точках М и К соответственно так, что АК = 4 см, ВМ = 6 см. Найдите периметр ABCD.

С1. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; угол BOD = 140 ° , угол DKB = 110 ° , угол ВМС = 90 ° . Найдите углы параллелограмма.

Ответ: угол С = угол А = 60 ° ; угол В = угол D = 120 ° .

ТЕМА: ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ

А1. Диагонали ромба составляют с его стороной углы, один из которых на 10 ° меньше другого. Чему равен больший угол ромба?

1) 55 ° 2) 100 ° 3) 110 ° 4) 80 °

А2. В прямоугольнике ABCD диагонали пересекаются в точке О. Е — середина стороны АВ, угол ВАС = 40 ° . Чему равен угол EOD?

1) 140 ° 2) 130 ° 3) 120 ° 4) 150 °

А3. В ромбе ABCD угол А равен 60 ° , АВ = 8 см. Из вершины В на стороны AD и CD проведены перпендикуляры ВМ и ВК соответственно. Чему равна сумма длин отрезков MD и СК?

1) 8 см 2) 10 см 3) 12 см 4) 4 см

А4. На сторонах АВ, ВС, CD и AD квадрата ABCD отмечены соответственно точки Р, М, Е и К так, что АР = ВМ = СЕ = DK = 5 см, угол АРК = 60 ° . Чему равен периметр четырехугольника РМЕК?

1) 20 см 2) 36 см 3) 24 см 4) 40 см

В1. В ромбе ABCD высота АК, проведенная к стороне ВС, пересекает диагональ BD в точке Е, угол ADE = 40 ° . Найдите величину угла ЕАС.

В2. Внутри квадрата ABCD выбрана точка М так, что треугольник AMD равносторонний. Найдите величину угла АМВ.

С1. Через середину диагонали КМ прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, пересекающая стороны KL и MN в точках А и В соответственно. Известно, что АВ = ВМ = 6 см. Найдите большую сторону прямоугольника.

А1. Диагонали ромба составляют с его стороной углы, один из которых на 35 ° меньше другого. Чему равен меньший угол ромба?

1) 70 ° 2) 55 ° 3) 60 ° 4) 85 °

А2. В прямоугольнике МРКН диагонали пересекаются в точке О. Отрезок ОА является высотой треугольника МОР, угол АОР = 15 ° . Чему равен угол ОНК?

1) 105 ° 2) 150 ° 3) 135 ° 4) 75 °

А3. В ромбе ABCD угол А равен 30 ° . Из вершины В на стороны AD и CD проведены перпендикуляры ВМ и ВК соответственно. ВМ = 4 см. Чему равен периметр ромба?

1) 40 см 2) 24 см 3) 32 см 4) 50 см

А4. На сторонах АВ, ВС, CD и AD квадрата ABCD отмечены соответственно точки Р, М, Е и К так, что АР = ВМ = СЕ = DK = 3 см, угол ВМР = 60 ° . Чему равен периметр четырехугольника РМЕК?

1) 32 см 2) 18 см 3) 24 см 4) 8 см

В1. В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС и диагональ BD соответственно в точках М и N, угол АМС = 120 ° . Найдите величину угла ANB.

В2. Внутри квадрата ABCD выбрана точка Е так, что треугольник ВЕС равносторонний. Найдите величину угла EAD.

С1. Через середину диагонали АС прямоугольника ABCD перпендикулярно этой диагонали проведена прямая, пересекающая стороны ВС и AD в точках К и Е соответственно. Известно, что КЕ = АЕ = 8 см. Найдите большую сторону прямоугольника.

ТЕМА: СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА И ТРАПЕЦИИ

ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ

А 1. В треугольнике АВС, ВС = 36 см. Через точку М, которая делит сторону АС так, что АМ : МС = 5 : 7, проведена прямая ML параллельно прямой АВ, пересекающая ВС в точке L. Найдите LC.

1) 11 2) 18 3) 20 4) 21 5) невозможно найти

А2. Боковая сторона AD трапеции ABCD равна 51 см. Через точку М, которая делит боковую сторону ВС так, что ВМ : МС = 11 : 6, проведена прямая MN параллельно основанию АВ, пересекающая AD в точке N. Найдите AN.

1) 33 2) 22 3) 11 4) 6 5) невозможно найти

А3. Диагонали четырёхугольника равны 120 см и 248 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.

1) 240 2) 368 3) 496 4) 128 5) невозможно найти

А4. Дан произвольный четырёхугольник АВМТ (никакие пары противоположных сторон не параллельны). Точки L и Н — середины отрезков АМ и МВ. Точки G и Y — середины отрезков АТ и ВТ. Найдите периметр четырёхугольника LHYG, если АВ + МТ = 20.

1) 40 2) 30 3) 20 4) 10 5) невозможно найти

В1. В трапеции ABCD на боковой стороне CD отмечена точка Н так, что СН : HD = 2 : 5. Прямая HG, параллельная основаниям ВС и AD, пересекает сторону АВ в точке G. Найдите GH, если ВС = 14, AD = 21.

В2. В треугольнике АВС на стороне ВС отмечена точка D так, что CD : DB = 1 : 2. В каком отношении прямая, проходящая через точку В и середину отрезка AD делит сторону АС, считая от точки А.

А1. В треугольнике ВЕС,ЕС=56см.Через точку М, которая делит сторону ВС так, что ВМ:ВС=3:8,проведена прямая МК параллельно прямой ВЕ, пересекающая ЕС в точке К. Найдите КС .

1) 10 2) 25 3) 20 4) 35

А2.Боковая сторонаАВ трапеции АВСD равна 28см.Через точку М,которая делит боковую сторону СD так,что СМ:МD =5:9,проведена прямая МЕ параллельно основанию АD,пересекающаяАВ в точке Е.Найдите ВЕ.

1) 10 2) 28 3) 18 4) 9

А3.Диагонали четырёхугольника равны320см и 68см.Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.

1) 640 2) 388 3) 136 4) 252

А4.Дан произвольный четырёхугольник АВРС(никакие пары противоположных сторон не параллельны).Точки Д и Е- середины отрезковАР и РВ.Точки M и N – середины отрезков АС и ВС.Найдите периметр четырёхугольника MДЕN, если АВ+РС=40

1) 10 2) 20 3) 30 4) 40

В1.В трапеции АВСД на боковой стороне СД отмечена точка Е так, что СЕ:ЕД=7:2.Прямая ЕК, параллельная основаниям ВС и АД, пересекает сторонуАВ в точке К. Найдите КЕ, еслиВС=9,АД=36.

В2.В треугольнике АВС на стороне АВ отмечена точка Е так, что АЕ:ЕВ=4:3. В каком отношении прямая, проходящая через точку А и середину отрезка СЕ делит сторону ВС,считая от точки В.

А1. В трапеции ABCD основания равны 12 см и 16 см. Чему равна ее средняя линия?

1) 26 см 2) 14 см 3) 8 см 4) 6 см

А2. В трапеции ABCD угол В = 116 ° , угол С = 125 ° . Чему равна сумма градусных мер углов А и D?

1) 119 ° 2) 241 ° 3) 193 ° 4) 166 °

А3. В трапеции ABCD из вершины угла В проведена прямая, параллельная стороне CD и пересекающая сторону AD в точке К так, что угол АКВ = 60 ° , угол А = 35 ° . Чему равен угол BCD?

1) 65 ° 2) 35 ° 3) 120 ° 4) 115 °

А4. В равнобедренной трапеции высота образует с боковой стороной угол 30 ° , а ее основания равны 10 см и 6 см. Чему равен периметр трапеции?

1) 28 см 2) 24 см 3) 26 см 4) 32 см

В1. В трапеции ABCD AD и ВС — основания, AD ВС. На стороне AD отмечена точка М так, что МBCD — параллелограмм. Периметр трапеции равен 22 см, DМ = 5 см. Найдите периметр треугольника АВМ.

В2. В равнобедренной трапеции ABCD диагональ BD перпендикулярна боковой стороне, угол А = 60 ° , AD = 14 см, ВС = 12 см. Найдите периметр трапеции.

С1. В прямоугольной трапеции диагональ перпендикулярна боковой стороне, острый угол равен 45 ° . Найдите отношение оснований.

А1. В трапеции ABCD основания равны 10 см и 16 см. Чему равна ее средняя линия?

1) 26 см 2) 13 см 3) 8 см 4) 6 см

А2. В трапеции ABCD угол В = 128 ° , угол С = 115 ° . Чему равна сумма градусных мер углов А и D?

1) 117 ° 2) 243 ° 3) 193 ° 4) 167 °

А3. В трапеции ABCD из вершины угла В проведена прямая, параллельная стороне CD и пересекающая сторону AD в точке К так, что угол АКВ = 65 ° , угол А = 35 ° . Чему равен угол BCD?

1) 65 ° 2) 35 ° 3) 100 ° 4) 115 °

А4. В равнобедренной трапеции высота образует с боковой стороной угол 30 ° , а ее основания равны 11 см и 5 см. Чему равен периметр трапеции?

1) 28 см 2) 27 см 3) 26 см 4) 32 см

В1. В трапеции ABCD AD и ВС — основания, AD ВС. На стороне AD отмечена точка Е так, что EBCD — параллелограмм. Периметр трапеции равен 32 см, DЕ = 5 см. Найдите периметр треугольника АВЕ.

В2. В равнобедренной трапеции ABCD диагональ BD перпендикулярна боковой стороне, угол А = 60 ° , AD = 24 см, ВС = 12 см. Найдите периметр трапеции.

Тест по теме: «Четыре замечательные точки треугольника»
вариант 1

Теорема: Каждая точка биссектрисы неразвернутого угла _______________________ от его сторон.

Серединным перпендикуляром к отрезку называется ____________, проходящая через _________________ данного отрезка и перпендикулярна к нему.

Обратная теорема: Каждая точка, ______________________ от концов отрезка, лежит на серединном _________________________ к нему.

Серединные перпендикуляры к сторонам треугольника пересекаются ___________________________.

Нарисуйте в треугольнике АВС серединные перпендикуляры и отметьте их точку пересечения буквой О.

Тест по теме: «Четыре замечательные точки треугольника»

Обратная теорема: Каждая точка, лежащая внутри угла и ______________________ от сторон угла, лежит наего _______________________.

Биссектрисы треугольника пересекаются ______________________ .

Теорема: Каждая точка серединного ____________________ к отрезку ____________________ от концов этого отрезка.

Высоты треугольника (или их продолжения) пересекаются ______________________.

Нарисуйте в треугольнике АВС высоты и отметьте их точку пересечения буквой О.

ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ТЕМЕ: ЧЕТЫРЕХУГОЛЬНИКИ

А1. Сумма углов выпуклого n-угольника равна:

1) 180°(n − 2) 2) 360° 3) 180° · n 4) 360° · n

А2. Четырехугольник является параллелограммом, если у него:

1) две стороны равны, а две другие параллельны

2) диагонали пересекаются и точкой пересечения делятся пополам

3) две пары равных сторон

4) все стороны параллельны

А3. Трапеция называется равнобедренной, если у нее:

1) две стороны равны 2) два угла равны 3) основания параллельны и равны

4) боковые стороны равны

А4. Прямоугольником называется:

1) параллелограмм, у которого все стороны равны

2) параллелограмм, у которого все углы прямые

3) четырехугольник, у которого диагонали равны

4) четырехугольник, у которого противолежащие стороны равны

А5. Четырехугольник является ромбом, если у него:

1) диагонали перпендикулярны

2) диагонали равны

3) диагонали перпендикулярны и точкой пересечения делятся пополам

4) диагонали точкой пересечения делятся пополам

А6. Квадратом является:

1) параллелограмм, у которого все углы прямые

2) ромб, у которого все углы прямые

3) параллелограмм, у которого диагонали равны

4) прямоугольник, у которого диагонали равны

А7. Всякий прямоугольник является:

1) квадратом 2) ромбом 3) трапецией 4) параллелограммом

А8. Выберите верное утверждение:

1) если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник — прямоугольник

2) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб

3) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник — прямоугольник

4) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат

А9. Внешний угол правильного n-угольника равен:

1) 180° / n 2) 180° (n − 2)/n 3) 360° (n − 2)/n 4) 360° / n

А10. Многоугольник называется выпуклым, если:

1) все его стороны являются выпуклыми

2) его нельзя разрезать на два других многоугольника

3) он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины

4) все его углы являются выпуклыми

1.Какая фигура обладает следующими свойствами:

— все углы прямые;

— диагонали пересекаются под прямым углом и является биссектрисами его углов?

А. Прямоугольник Б. Ромб В. Квадрат Г. Параллелограмм

2. Прямоугольник, у которого все стороны равны – это

А. Прямоугольник Б. Ромб В. Квадрат Г. Параллелограмм

3.Четырехугольник, вершины которого находятся в серединах сторон прямоугольника.

А. Произвольный параллелограмм Б. Прямоугольник В. Ромб Г. Квадрат

4.Из каких двух равных треугольников можно сложить квадрат?

А. Прямоугольных Б. Правильных В. Равнобедренных Г. Равнобедренных прямоугольных

5. В ромбе одна из диагоналей равна его стороне. Углы ромба:

А. 30°, 60°, 30°, 60° Б. 45°, 45°, 135°, 135° В. 60°, 60° , 120°, 120°

Г. 30°, 150°, 30°, 150°

6. Сумма двух углов параллелограмма 134°. Найдите его углы.

А. 134°, 134°, 46° 46° Б. 67°, 67°, 113°, 113° В. 67°, 67°, 134°, 134°

Г. 67°, 113°, 134°, 46°

7. В прямоугольнике перпендикуляры, проведенные из точки пересечения диагоналей к его сторонам, равны соответственно 3см и 5 см. Найдите периметр прямоугольника.

А. 16см Б. 24см В. 32см Г. 48 см

8. Периметр параллелограмма 36см. Одна из сторон 12см. Найти остальные стороны.

А. 12, 12, 6, 6 Б. 12, 18, 12, 6 В. 12, 6, 10, 8 Г. 12, 12, 8, 8

9. В равнобокой трапеции диагональ перпендикулярна к ее боковой стороне и образует с основанием угол 15°. Найдите углы трапеции.

А. 30° , 150° , 30°, 150° Б. 75°, 105°, 75°, 105° В. 45°, 135°, 45°, 135°

10. В ромбе перпендикуляр, проведенный из вершины тупого угла, делит сторону пополам. Найдите углы ромба.

А. 60°, 60°, 120°, 120° Б. 45°, 45°, 135°, 135° В. 90°, 90° , 90°, 90°

Г. 30°, 30°, 150°, 150°

ТЕМА: СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ

А1. В треугольнике АВС угол С = 90°, угол А = 32°, ВС = 4 см. Найдите длину АС.

1) 4 · cos32° 2) 4 : tg32° 3) 4 · tg32° 4) 4 : sin32°

А2. sin α = 5/13. Найдите tg α.

1) 5/12 2) 12/13 3) 12/5 4) 13/12

А3. В треугольнике КСР (КС = СР) угол С = 70°, КС = 12 см. Найдите длину КР.

1) 12 · cos35° 2) 6 · cos35° 3) 24 · sin35° 4) 24 : sin35°

А4. Вычислите значение выражения sin 2 60° − 3tg45°.

1) −2,25 2) −1,25 3) −0,75 4) −1,5

В1. В треугольнике АВС угол С = 90°, CD — высота, угол А = α, АВ = k. Найдите длины АС, ВС, AD.

Ответ: АС = k · cosα; BC = k · sinα; AD = k · cos 2 α.

В2. Стороны параллелограмма равны 4 см и 5 см, угол между ними 45°. Найдите высоты параллелограмма.

Ответ: 2√2 см; 2,5√2 см.

С1. В прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона — 2√3. Найдите площадь трапеции, если один из ее углов равен 120°.

С2. В равнобедренном треугольнике АВС (АВ = ВС) угол А = 30°. Найдите высоту, опущенную к основанию, если AD = 20 см (D принадлежит прямой АВ, а CD перпендикулярен АВ).

А1. В треугольнике АВС угол С = 90°, угол В = 40°, ВС = 9 см. Найдите длину АС.

1) 9 : tg40° 2) 9 · cos40° 3) 9 : sin60° 4) 9 · tg40°

А2. cos α = 8/17. Найдите tg α.

1) 9/8 2) 15/8 3) 8/15 4) 8/9

А3. В треугольнике CDE (CD = DE) угол D = 68°, СЕ = 10 см. НайдитедлинуCD.

1) 5 · sin34° 2) 10 :sin68° 3) 8 · cos51° 4) 5 : sin34°

А4. Вычислите значение выражения cos 2 45° − 4sin30°.

1) −2 2) −3 3) −1,5 4) −2,5

В1. В треугольнике MNP угол Р = 90°, РК — высота, угол N = β, PN = b. Найдите длины MN, MP, KN.

Ответ: MN = b :cosβ; MP = b · tgβ; KN = b · cosβ.

В2. Стороны параллелограмма равны 6 см и 7 см, угол между ними 60°. Найдите высоты параллелограмма.

Ответ: 3√3 см; 3,5√3 см.

С1. В равнобедренной трапеции меньшее основание равно 8, а высота — √3. Найдите площадь трапеции, если один из ее углов равен 150°.

С2. В равнобедренном треугольнике АВС с основанием АС угол при вершине равен 120°, CD — высота. Найдите длину AD, если высота, проведенная к основанию, равна 10 см.

1.Вставьте пропущенные слова, чтобы получилось верное высказывание

Косинусом острого угла ….. треугольника называется отношение ….. катета к гипотенузе.

2. В прямоугольном треугольнике один из острых углов 30°, а гипотенуза равна 12 см. Найдите меньший катет этого треугольника.

а) 6 см б) 6√3 см в) 18 см г) другой ответ

3. В прямоугольном треугольнике угол С =90, АС=28 см, АВ=35 см.

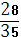
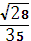
а)другой ответ. б) в); г).

4. В треугольнике АВС, угол С равен 90°, sin А= . Найти cosA.

5. В треугольнике АВС угол С равен 90°, АС = 7, АВ = 25

а) ; б) ; в) ; г) .

6. В треугольнике АВС угол С=90, АС=4,8 cosA=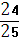. Найти АВ.

7. В треугольнике АВС угол С=90°. СА= 6 см, СВ=2см. Найти угол A

8. Напишите соотношение

1) соs -30: 2) 60; 3)sin 30; 4) sin45.

a); в:

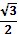
б) 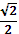; г) .

Вставьте пропущенное слово, чтобы получилось верное высказывание

Синусом острого угла треугольника называется отношение ….. катета к гипотенузе.

В прямоугольном треугольнике один из острых углов 60°, а прилежащий катет равен 8. Найти гипотенузу

В треугольнике угол С=90, АВ=50, ВС=30. Найти cosА.

б) 0,8 б) 0,5

В треугольнике АВС, угол С=90, cos А=0,4. Найти sin А.

В треугольнике АВС, угол С=90, АВ=20, ВС=16. Найти sin А.

а) 0,7 в) 0,8

б) 1 г) 0,5

В треугольнике АВС угол С=90, sinA= , ВС= . Найти АВ.

б) 0,5 г) другой ответ.

В треугольнике АВС угол С=90 АС=12 см, СВ=15. Найти tgA

а) 0,8 б) 5/4 в) 4/3 г) 3/4

сos 60 2) tg 60 3) sin 60 4) cos 45

а) ; б) в) г)

ТЕМА: ТЕОРЕМА ПИФАГОРА

А1. В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему равна его гипотенуза?

1) 9 см 2) 10 см 3) 11 см 4) 12 см

А2. В прямоугольнике ABCD смежные стороны относятся как 12 : 5, а его диагональ равна 26 см. Чему равна меньшая сторона прямоугольника?

1) 24 см 2) 20 см 3) 16 см 4) 10 см

А3. Один из внешних углов прямоугольного треугольника равен 135°, а его гипотенуза — 6см. Чему равны катеты данного треугольника?

1) 4 см и 4 см 2) 2 см и 2 см 3) 3 см и 3 см 4) 3√2 см и 3√2 см

А4. Диагонали ромба равны 12 см и 16 см. Чему равна сторона ромба?

1) 21 см 2) 10 см 3) 15 см 4) 20 см

В1. Большая диагональ прямоугольной трапеции равна 25 см, а большее основание — 24 см. Найдите площадь трапеции, если ее меньшее основание равно 8 см.

В2. Основания равнобедренной трапеции равны 10 см и 26 см, а боковая сторона равна 17 см. Найдите площадь трапеции.

С1. В параллелограмме ABCD BD = 2√41 см, АС = 26 см, AD = 16 см. Через точку пересечения диагоналей параллелограмма О проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону AD.

Ответ: 4 см; 12 см.

А1. В прямоугольном треугольнике катеты равны 12 см и 5 см. Чему равна его гипотенуза?

1) 14 см 2) 11 см 3) 13 см 4) 12 см

А2. В прямоугольнике ABCD смежные стороны относятся как 3 : 4, а его диагональ равна 20 см. Чему равна большая сторона прямоугольника?

1) 16 см 2) 12 см 3) 14 см 4) 15 см

А3. Один из внешних углов прямоугольного треугольника равен 135°, а его гипотенуза — 5√2 см. Чему равны катеты данного треугольника?

1) 4 см и 4 см 2) 5 см и 5 см 3) 3 см и 3 см 4) 5√2 см и 5√2 см

А4. Диагонали ромба равны 12 см и 16 см. Чему равна сторона ромба?

1) 10 см 2) 20 см 3) 15 см 4) 14 см

В1. Большая диагональ прямоугольной трапеции равна 17 см, а большее основание — 15 см. Найдите площадь трапеции, если ее меньшее основание равно 9 см.

В2. Основания равнобедренной трапеции равны 10 см и 24 см, а боковая сторона равна 25 см. Найдите площадь трапеции.

С1. Две окружности радиусов 13 см и 15 см пересекаются. Расстояние между их центрами О₁ и О₂ равно 14 см. Общая хорда этих окружностей АВ пересекает отрезок О₁О₂ в точке К. Найдите О₁К и КО₂ (О₁ — центр окружности радиуса 13 см).

Тест по теме «Декартовы координаты на плоскости»

№1. Точка С – середина отрезка АВ. найдите ее координаты, если А(-2; -2), В(3; 2).

А) (-0,5; 0); Б) (0; 1); В) (0,5; 0); Г) (1; 0).

№2. Найдите диагональ квадрата АВСD, если А(0; 4), В(4; 4), С(4; 0), D(0; 0).

А) ; Б) 32; В) 16; Г) 8.

№3. Найдите координаты центра и радиус окружности

А) О(0;0), R=2; Б) О(5;0), R=2;

Найдите точку пересечения прямых, которые заданы уравнениями: 2х+3у+5=0 и 2х+2у+6=0.

Даны точки А(0; 1), В(2; 5), С(4; 1), D(2; -3).

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

ГДЗ по геометрии 8 класс Гаврилова контрольно-измерительные материалы

Авторы: Гаврилова Н.Ф.
ВАКО

Контрольно-измерительные материалы по геометрии за 8 класс автора Гавриловой Н.Ф. 2011 года издания. Пособие по своему объему небольшое и охватывает 65 страниц. Сюда отнесены многочисленные темы, расписанные детально. К ним прикреплены разнообразные рисунки и графики, помогающие быстрее освоить изучаемый материал.

При изучении данного предмета в школе школьникам следует позаботиться о дополнительной литературе. Абсолютно все готовые решения в этом пособии полностью соответствуют тематическим требованиям упражнений. Выполненные работы рассчитаны для текущего и итогового контроля знаний учащихся.

В предлагаемом сборнике рассмотрены задания на такие темы: «Многоугольники», «Параллелограмм», «Трапеция», «Прямоугольник. Ромб. Квадрат», «Площадь многоугольника. Площадь прямоугольника». Также решены задачи из разделов «Площадь параллелограмма, ромба и треугольника» и «Площадь трапеции».

В решебник вошли такого характера готовые задания: чему равна сумма углов выпуклого шестиугольника; найдите большую сторону прямоугольника; чему равна сумма выпуклого пятиугольника; найдите наименьший угол параллелограмма и многие другие.