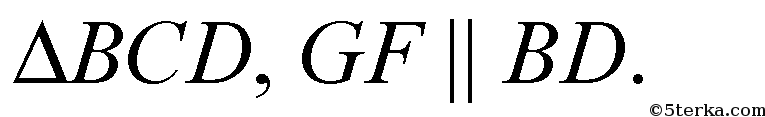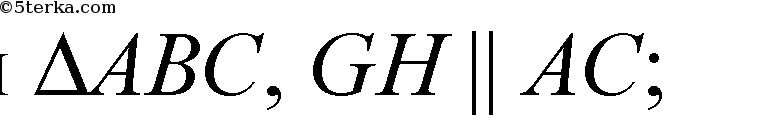Через любые две стороны пространственного четырехугольника можно провести плоскость

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №43
к главе «Глава I Параллельность прямых и плоскостей. §2 Взаимное расположение прямых в пространстве. Угол между двумя прямыми.».

* Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости.

Соединим все вершины пространственного четырехугольника.

НЕ – средняя линия ΔBAD,

GH – средняя линия

EF – средняя линия

4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом, следовательно, EFGH -параллелограмм (из параллельности сторон также следует, что четырехугольник плоский).

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Пространственный четырехугольник

Пространственный четырехугольник описан около сферы. [1]

В случае пространственного четырехугольника можно показать, что существуют сферы, касающиеся самих сторон, а не их продолжений. [2]

Около сферы описан пространственный четырехугольник . [3]

Рассмотрим теперь некоторый пространственный четырехугольник K . LNM ( рис. 9 – 4, б), построенный на двух взаимно перпендикулярных проводниках KL и MN, не лежащих в одной плоскости. [4]

Легко заметить, что пространственный четырехугольник ABCD представляет силовой многоугольник, построенный на силах Pj, P2 и Р3, причем диагональ параллелепипеда AD есть замыкающая сторона. [5]

Отсюда следует, что существует замкнутый пространственный четырехугольник A B CJ), стороны которого таковы, что A1Bix, B1C1 y C1D1 z, DlAl – t, и, следовательно, сумма площадей трех любых граней тетраэдра ABCD больше площади четвертой грани. [6]

Доказать, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. [7]

Показать, что в этом случае всякий пространственный четырехугольник , две противоположные вершины которого лежат на окружности С, а две другие – на окружности С, обладает тем свойством, что произведение одной пары его противоположных сторон равно произведению сторон другой пары. [8]

Точки К, L, М и N сторон пространственного четырехугольника ARCD удовлетворяют условиям BK BL, CL CM, f M DN и ANAK. Но плоскость Р перпендикулярна к отрезку NK ( вытекает из того, что ANAK) и, следовательно, перпендикулярна к плоскости KLMN. Плоскости О, R и S также перпендикулярны по аналогичным причинам к плоскости KLMN. Так как плоскости Р, Q, R и S имеют общую точку О и перпендикулярны к плоскости KLMN, то они проходят через одну прямую. [9]

Прямые, которые соединяют две точки, взятые на двух смежных сторонах пространственного четырехугольника , с точками, делящими соответственно в тех же отношениях стороны, противоположные первым, пересекаются; отрезок каждой из этих прямых, заключенный между сторонами четырехугольника, делится другой прямой в том же отношении, как и те стороны, которых первая прямая не пересекает. [10]

Итак, существует, вообще говоря, восемь шаров, касающихся всех сторон пространственного четырехугольника или их продолжений. [11]

Пусть требуется найти шар, касающийся четырех сторон АВ, ВС, CD и DA пространственного четырехугольника или их продолжений, иначе говоря, шар, касающийся четырех прямых АВ, ВС, CD и DA, не лежащих в одной плоскости. Будем называть такой шар для краткости касательным шаром и обозначим его центр через О. [12]

Покажем прежде всего, что при этом условии существует точка, равноудаленная от всех сторон пространственного четырехугольника ABCD и от прямой АС. [13]

Во втором случае, когда опорные точки каркаса соединяют кривыми линиями ( рис. 161, в), криволинейный пространственный четырехугольник , состоящий из четырех соединенных дуг различной конфигурации, можно затянуть гладкой поверхностью. Граничные дуги стягивают хордами. Для некоторой текущей точки М строят координатные плоскости х XM и у УМ и в них-трапеции. Нижние стороны трапеций пересекаются в точке S. [14]

Интересно отметить, что в этой теореме можно считать любой четырехугольник даже пространственным четырехугольником , у которого пары прилежащих сторон лежат в четырех различных плоскостях. [15]

Что ты хочешь узнать?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Ответ

Проверено экспертом

M, N, L и K середины сторон AB, BC, CD и DA соответственно.

Отрезок соединяющий середины двух сторон в треугольнике является средней линией, которая параллельна третьей стороне.

MN, NL, LK и KM среднии линии в ΔABC, ΔBCD, ΔCDA и ΔDAB соответственно. Значит MN║AC; NL║BD; LK║CA=AC; KM║DB=BD.

MN║AC║LK ⇒ MN║LK – по транзитивности параллельных прямых а пространстве.

Так же NL║KM (NL║BD║KM).

В четырёхугольнике MNLK противоположные стороны параллельны (MN║LK и NL║KM), то есть это параллелограмм. А точки M, N, L и K его вершины. Доказано.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Через любые две стороны пространственного четырехугольника можно провести плоскость

1. Какое из следующих утверждений верно?

а) любые четыре точки лежат в одной плоскости; б) любые три точки не лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость; д) через любые три точки проходит плоскость, и притом только одна.

2. Сколько общих точек могут иметь две различные плоскости?

а) 2; б) 3; в) несколько; г) бесконечно много; д) бесконечно много или ни одной.

3. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных

плоскостей при этом получилось?

а) 2; б) 3; в) 1; г) 4; д) бесконечно много .

4. Если три точки не лежат на одной прямой, то положение плоскости в пространстве они:

а) не определяют в любом случае; б) определяют, но при дополнительных условиях;

в) определяют в любом случае; г) ничего сказать нельзя; д) другой ответ.

5. Выберите верное утверждение.

а) Если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна; в) через две пересекающиеся прямые плоскость провести нельзя; г) любые две плоскости не имеют общих точек; д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой.

Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Школьная лекция по теме «Параллельность в пространстве» 10 класс

Видео:Классная задача о пространственном четырёхугольнике, описанном около сферыСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тема: «Параллельность в пространстве» Урок-лекция 10 класс

Основные определения: две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются. две плоскости называются параллельными, если они не пересекаются. плоскость и прямая называются параллельными, если они не пересекаются.

Теоремы-признаки Две прямые параллельны между собой, если они каждая параллельны третьей прямой. Если прямая, не принадлежащая плоскости параллельна какой-либо прямой в этой плоскости, то она параллельна самой плоскости. Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой.

Теорема –признак параллельности прямой и плоскости. Если прямая, не лежащая в плоскости , параллельна какой-то прямой в плоскости, то она параллельна всей плоскости. Доказательство: Пусть есть прямая а в плоскости α , а вне её есть прямая в, причём а//в. Докажем , что в//α. Пусть не параллельна, тогда прямая в пересекает плоскость в некоторой точке С. Так как через две пересекающиеся прямые проходит плоскость β, то плоскость α имеет с плоскостью β общую точку С, а значит пересекается по прямой а. Тогда через точку С проходят две различные прямые, которые по предположению пересекаются, а по условию параллельны. Этого быть не может, значит, предположение не верно, и прямая а//α.

Теорема-признак параллельности плоскостей Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой. Пусть плоскости пересекаются. Тогда прямая с принадлежит и плоскости α и плоскости β. Получается, что если сα, то с//а и с//в, лежащих в плоскости β , так как если прямая параллельна плоскости, тогда она параллельна любой прямой этой плоскости. Значит, через точку С проходит две различные параллельные прямые. Что является противоречием, а значит плоскость α параллельна плоскости β.

Теоремы (для построения) Через точку вне прямой можно провести прямую параллельную данной и только одну. Через точку вне плоскости можно провести плоскость параллельную данной и только одну. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны. Отрезки параллельных прямых, заключённые между двумя параллельными прямыми равны между собой .

Изображение пространственных фигур. Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проек­цией в направлении этой прямой является точка. Если прямая не парал­лельна и не совпадает с прямой l, то ее проекцией является прямая. Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при парал­лельном проектировании середина отрезка переходит в середину соответствующего отрезка. Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или од­ной прямой. Свойство 4. Если плоская фигура F лежит в плоскости, параллель­ной плоскости проектирования π, то ее проекция F’ на эту плоскость бу­дет равна фигуре F. Пусть F — некоторая фигура в пространстве. Проекции ее точек на плоскость α образуют фигуру F ‘, которая называется параллельной проек­цией фигуры Ф на плоскость α в направлении прямой l. Говорят также, что фигура F ‘ получена из фигуры F параллельным проектированием.

Основное правило: параллельность и отношение длин сохраняется, длины отрезков и углы, не сохраняются . на основании этого правила скажите квадрат изображается? прямоугольник изображается? параллелограмм изображается? медиана изображается? высота изображается? Круг изображается овалом или эллипсом .

Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или многоугольник с тем же числом сторон или отрезок. Причем, если в многоугольнике какие-нибудь две стороны параллельны, то их проекции также будут параллельны. При параллельном проектировании длины отрезков и углы, не сохраняются, проекцией равностороннего треугольника может быть треугольник с разной длиной сторон, проекцией прямоугольно­го треугольника может быть не прямоугольный треугольник. Проекцией параллелограмма является параллелограмм, проекцией пря­моугольника может не быть прямоугольник, проекцией ромба не обязательно является ромб, проекцией правильного многоугольника может быть неправильный многоугольник.

Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограмма­ми параллелепипед куб Прямоугольный параллелепипед

Для того чтобы построить изображение призмы, достаточно постро­ить многоугольник, изображающий ее основание. Затем из вершин многоу­гольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, полу­чим многоугольник, являющийся изображением второго основания призмы

Для того чтобы построить изображение пирамиды, достаточно пост­роить многоугольник, изображающий ее основание. Затем выбрать ка­кую-нибудь точку, которая будет изображать вершину пирамиды, и соеди­нить ее с вершинами многоугольника. Полученные отрезки бу­дут изображать боковые ребра пирамиды.

Упражнения 1. В каком случае параллельной проекцией прямой будет точка? Ответ: Если прямая параллельна направлению проектирования. 2. В каком случае параллельной проекцией двух параллельных прямых является одна прямая? Ответ: Если плоскость, в которой лежат эти прямые, параллельна направлению проектирования. 3. Какие фигуры могут быть параллельными проекциями двух скре­щивающихся прямых? Ответ: Две пересекающиеся прямые; две параллельные прямые; прямая и точка, ей не принадлежащая. 4. Сохраняются ли при параллельном проектировании: а) длины отрезков; б) величины уг­лов? Ответ: а), б) Нет.

5. Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования? Ответ: Нет. 6. Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник? Ответ: а), б), в) Да. 7. Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция? Ответ: а), б), в) Да; г) нет. 8. Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы? Ответ: а) Да; б), в) нет.

Параллельными проекциями каких многогранников являются фигуры, изображенные на рисунке? Ответ: а), б) 4-я пирамида; в) тетраэдр; г), д) 6-я пирамида; е) параллелепипед.

Верно ли? Для любых двух прямых можно провести плоскость, параллельную каждой из них.(нет, случай перпендикулярности прямых). Все прямые , проходящие через данную точку, параллельно данной плоскости, лежат в одной плоскости.(да). Сохраняется ли при параллельном проектировании отрезков одной плоскости их отношение?(да) Может ли при параллельном проектировании трапеции получиться прямоугольник? (нет). Может ли при параллельном проектировании параллелограмма получиться прямоугольник?(да) Может ли параллельная проекция произвольного параллелограмма быть ромбом? (нет) Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в плоскости? (нет)

Какая из указанных фигур не может быть параллельной проекцией правильного треугольника, в котором построена одна высота?

Какая из указанных фигур не может быть проекцией пространственного четырёхугольника?

Каково взаимное расположение а и в?АДα. ВС по отношению к α?

АДα..МNпо отношению к ВС?

В пространстве даны прямая и точка А. Сколько существует прямых, которые проходят через А и параллельны прямой. Через стороны АВ и СД четырёхугольника АВСД и точку К вне его проведены две плоскости , пересекающиеся по прямой параллельной каждой из прямых АВ иСД. Установите вид четырёхугольника АВСД, если известно, что АВ=СД.

С А В F N M К Дано: F ∉ АВС. FА, FВ, FС. АМ=MF, BK=FK, FN=NC. Выбрать три пары параллельных прямых. Доказать, что они параллельны.

С А В F N M К Дано:∆ АВС, F ∉ (АВС) M∈AF, K∈FB, N∈FC FM:MF=FK:KB=FN:NC Доказать, что (ABC)||(MNK)

В С С₁ В₁ А α Дано :α ∩ AB=B₁; α ∩ AC=C₁ AB₁:B₁C₁=2:3, BC=15 см, ВВ₁=6 см BC||α Найти: В₁С₁

α M N A B C D Дано : АВСD- трапеция α││АD; α∩АВ=М ,α∩ СД=N AM=MB, CN=ND. BC=9 см , AD= 17см Найти :MN

Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1 , В1 и С1. Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7. α А В С А1 В1 С1

💥 Видео

10 класс, 2 урок, Аксиомы стереометрииСкачать

Средние линии пространственного четырёхугольникаСкачать

Решение задач пространственный четырехугольникСкачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Пространственные фигуры. Прямые и плоскости. 10 класс. Вебинар | МатематикаСкачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

Построение следов плоскостиСкачать

Линия пересечения плоскостейСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Пространственные фигуры. Прямые и плоскости. Математика 10 класс. Вебинар | TutorOnlineСкачать

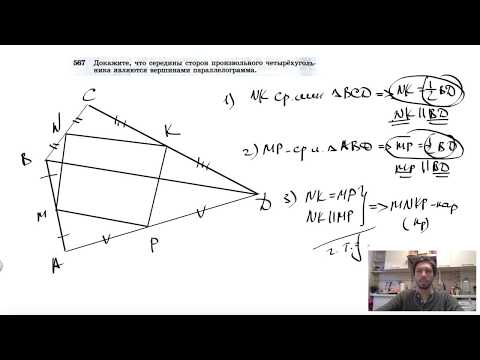
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать