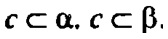Через каждую из двух параллельных прямых проведена плоскость эти две плоскости пересекаются как (5 видео)

Даны две параллельные прямые. Через каждую из них проведена плоскость. Эти две плоскости пересекаются. Как расположена их линия

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Докажите, что эти плоскости пересекаются. Дополнительные задачи 91, Геометрия, 10-11 класс, Атанасян Л.С.
Введение. Аксиомы стереометрии и их следствие. 5 часов (стр. 5 )
🎥 Видео

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Ваш ответ

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

решение вопроса

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Докажите, что эти плоскости пересекаются. Дополнительные задачи 91, Геометрия, 10-11 класс, Атанасян Л.С.

Нам с дочкой снова нужна ваша помощь :))

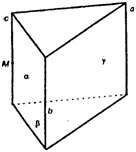
Через каждую из двух параллельных прямых а и b и точку М, не лежащую в плоскости этих прямых, проведена плоскость. Докажите, что эти плоскости пересекаются по прямой, параллельной прямым а и b.

Здравствуйте, я могу помочь
а || b
Из аксиомы А₃ (п. 2) следует существование прямой с, проходя щей через т. M, параллельной а и b.
α — плоскость, в которой лежат а и с; β — плоскость, в которой лежат с и b ;

то есть эта прямая и есть прямая пересечения α и β А по построению она параллельна прямым а и b.
Утверждение доказано.

Видео:№91. Через каждую из двух параллельных прямых a и b и точку М, не лежащую в плоскости этих прямыхСкачать

Введение. Аксиомы стереометрии и их следствие. 5 часов (стр. 5 )

Через каждую из двух параллельных прямых проведена плоскость эти две плоскости пересекаются как

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Доказать, что если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Дано: a || b, a α, b β,

α β = c.

1. по признаку а || β.

2. по предыдущему утверждению а || с.

3. Аналогично, b || c.

Доказать, что если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Доказать, что b || α либо b α.

Пусть b || α, следовательно b α.

Тогда по лемме a α.

Полученное противоречие опровергает предположение.

Постройте сечение тетраэдра ABCD плоскостью, проходящей через вершину С, внутреннюю точку М ребра АВ и параллельной прямой AD.

4. (MNC) – искомое сечение.

Найдите площадь полученного сечения, если каждое ребро тетраэдра имеет длину а и точка М является серединой ребра АВ.

Дано: ABCD – трапеция,

ВС = 12 см, М (АВС), ВK = KМ.

Доказать, что (ADK) МС = Н.

3. AD || BC, AD || KH KH || BC.

4. BK = KH, KH || BC CH = HM.

Следовательно, KН – средняя линия Δ BMC. KH = 6 см.

AB || α, C α.

CD α; MN || α, где MN – средняя линия трапеции.

1. Пусть CD α, тогда CD α = c.

по лемме AB α. Но AB || α.

Полученное противоречие опровергает предположение.

Следовательно, CD α.

2. по признаку MN || α.

Доказать, что α AC = M
и AM = CM.

№ 32 (разобрать доказательство самостоятельно).

Урок 6
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ,
ПРЯМОЙ И ПЛОСКОСТИ

Цели: систематизировать материал изученного параграфа; проверить уровень сформированности умения применять полученные знания к решению задач.

I. Проверка домашнего задания (у доски).

II. Устная работа.

1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости).

2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?

3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения.

4. Одна из двух параллельных прямых параллельна некоторой плоскости. Можно ли утверждать, что и вторая прямая параллельна этой плоскости? Ответ обоснуйте.

5. Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым?

6. Даны две скрещивающиеся прямые. Можно ли через одну из этих прямых провести плоскость, параллельную другой?

7. В плоскости α даны две пересекающиеся прямые а и b. Точка С не лежит в плоскости α. Каковы возможные случаи расположения прямой, проходящей через точку С, относительно прямых а и b?

8. Дано: FABCD – пирамида, ABCD – параллелограмм.

Каково взаимное расположение прямой пересечения плоскостей (FAD) и (FBC) и плоскости основания (АВС)?

III. Решение задач: №№ 90 (устно), 91, 92, 93, 96.

1. Через сторону АС треугольника АВС проведена плоскость α. В α. Докажите, что прямая, проходящая через АВ и ВС, параллельна плоскости α.

2. Дан Δ MKP. Плоскость, параллельная прямой МK, пересекает МР в точке М1, РK – в точке K1. Найдите М1K1, если МР : М1Р = 12 : 5, МK = 18 см.

3. Точка Р не лежит в плоскости трапеции ABCD (AD || BC). Докажите, что прямая, проходящая через середины РВ и РС, параллельна средней линии трапеции.

1. Через основание AD трапеции ABCD проведена плоскость α. ВС α. Докажите, что прямая, проходящая через середины сторон АВ и CD, параллельна плоскости α.

2. Дан Δ BCE. Плоскость, параллельная прямой СЕ, пересекает ВЕ в точке Е1, а ВС – в точке С1. Найдите ВС1, если С1Е1 : СЕ = 3 : 8, ВС =
= 28 см.

3. Точка Е не лежит в плоскости параллелограмма АВСD. Докажите, что прямая, проходящая через середины АЕ и ВЕ, параллельна прямой СD.

Урок 7
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ

Цель: доказать признак скрещивающихся прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой.

I. Работа над ошибками.

II. Объяснение нового материала. Вспомнить различные случаи взаимного расположения прямых в пространстве (урок № 6).

Рассмотреть различные пары скрещивающихся прямых на моделях многоугольников, наблюдая факт, зафиксированный в признаке скрещивающихся прямых.

Например, ABCDA1B1C1D1 – куб. АА1 и DC – скрещивающиеся ребра. В каких плоскостях лежит прямая CD? Как располагается прямая АА1 по отношению к этим плоскостям?

ABCA1B1C1 – призма. ВВ1 и А1С1 – скрещивающиеся ребра. В каких плоскостях лежит прямая ВВ1? Как располагается прямая А1С1 по отношению к этим плоскостям?

АBCD – пирамида. Рассуждаем аналогично. Наблюдаем: прямые являются скрещивающимися, если одна прямая лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой.

Если учащиеся упустили выделенный в формулировке факт, то привести контрпример – пересекающиеся прямые.