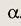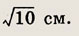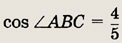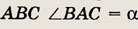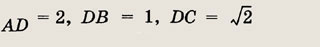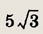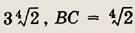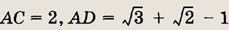Через две смежные вершины квадрата проведена окружность так что

2121. В круг радиуса R вписан равносторонний треугольник и квадрат, имеющие общую вершину. Вычислить площадь общей части треугольника и квадрата.

2122. В ромб вписана окружность, радиус которой равен R и в четыре раза меньше большей диагонали ромба. Определить площадь каждой из фигур, ограниченных отрезками двух смежных сторон ромба от вершины до точек касания и меньшей дугой окружности, лежащей между точками касания.

2123. Внутри треугольника ABC взята произвольная точка и через нее проведены три прямые, параллельные сторонам треугольника. Эти прямые делят треугольник ABC на шесть частей, из которых три части являются треугольниками. Площади этих треугольников равны S₁, S₂ и S₃.

Доказать, что площадь треугольника ABC равна (√ S ₁+ √ S ₂ + √ S ₃) 2

2124. Центры четырех кругов расположены в вершинах квадрата со стороной а. Радиусы этих кругов равны а. Определить площадь их общей части.

2125. В окружность радиуса R помещены три равные окружности, касающиеся внешней окружности и попарно друг друга. Вычислить площадь фигуры, ограниченной всеми тремя этими окружностями.

2126. Внутри окружности радиуса R расположены шесть равных окружностей меньшего радиуса. Каждая из них касается большей окружности и двух равных ей соседних окружностей. Вычислить площадь фигуры, ограниченной всеми шестью этими окружностями.

2127. Внутри окружности радиуса R расположены четыре равные окружности меньшего радиуса. Каждая из них касается большей окружности и двух равных ей соседних окружностей. Вычислить площадь фигуры, ограниченной всеми четырьмя этими окружностями.

2128. Сторона правильного треугольника равна а. Из его центра радиусом a /₃ описана окружность. Определить площадь части треугольника, лежащей вне окружности.

2129. Вычислить площадь треугольника по двум сторонам а и b и биссектрисе l угла между ними.

2130. Найти радиус круга, если площадь круга на q кв. единиц больше площади вписанного в него правильного двенадцатиугольника.

2131. Окружность радиуса R с центром в точке О разделена точками А, В, С, D, Е, F на шесть равных частей. Определить площадь фигуры СОЕ, ограниченной дугой ОС с центром в точке В, дугой ОЕ с центром в точке F и дугой СЕ с центром в точке А.

2133. Через две смежные вершины квадрата проведена окружность так, что касательная к ней, проведенная из третьей вершины, равна двойной стороне квадрата. Найти площадь этого квадрата, если радиус окружности равен R.

2134. Площадь треугольника ABC равна S₁; площадь треугольника АОВ, где О—точка пересечения высот, равна S₂. Точка К — такая точка на прямой СО, что треугольник АВК — прямоугольный. Доказать, что площадь треугольника АВК есть среднее геометрическое между S₁ и S₂.

2135. В равносторонний треугольник со стороной а вписана окружность. К окружности проведена касательная так, что отрезок ее внутри треугольника равен b. Найти площадь треугольника, отсеченного этой касательной от данного.

2136. Основания высот остроугольного треугольника ABC служат вершинами другого треугольника, периметр которого равен 2 р. Найти площадь треугольника ABC, если радиус описанной около него окружности равен R.

2137. Стороны треугольника ABC разделены точками М, N и Р так, что AM : MB = BN : NC = CP : PA =1 : 4. Найти отношение площади треугольника, ограниченного прямыми AN, BP и СМ, к площади треугольника ABC.

2138. Выразить площадь четырехугольника через четыре его стороны а, b, с, d и диагонали т, п. Имеет ли задача решение при меньшем числе данных величин?

2139. Найти площадь параллелограмма, стороны которого равны т и п, а расстояния от произвольной точки до четырех вершин равны а, b, с, d.

2140. Около окружности радиуса 5 см описана равнобочная трапеция. Расстояние между точками касания боковых сторон равно 8 см. Найти площадь трапеции.

2141. Через данную точку внутри угла провести прямую так, чтобы она отсекла от него треугольник наименьшей площади.

2142. В трапецию, у которой меньшее основание равно а, вписана окружность. Одна из боковых сторон трапеции делится точкой касания на отрезки длины т и п, считая от большего основания. Определить площадь трапеции.

2143. Даны два правильных треугольника, каждый площади S, из которых второй получается из первого поворотом на 30° около его центра. Вычислить площадь общей части этих треугольников.

2144. Площадь прямоугольного треугольника равна 2 /₃ r 2 , где r — радиус окружности, касающейся одного катета и продолжений другого катета и гипотенузы. Найти стороны треугольника.

2145. Вычислить площадь общей части двух ромбов, из которых второй получается поворотом первого на 90° около точки пересечения его диагоналей, если известно, что диагонали ромба равны 2 см и 3 см.

2146. Диагонали трапеции разбивают ее на четыре треугольника. Доказать, что если площади двух из них, прилежащих к основаниям трапеции, равны соответственно p 2 и q 2 , то площадь всей трапеции равна (р + q) 2

2147. В четырехугольнике ABCD через середину диагонали BD проведена прямая, параллельная другой диагонали АС. Эта прямая пересекает сторону AD в точке Е. Доказать, что отрезок СЕ делит площадь четырехугольника ABCD пополам.

2148. Большая из параллельных сторон трапеции равна а, меньшая равна b, непараллельные стороны равны c и d. Найти площадь трапеции.

2150. В прямоугольный треугольник ABC вписана окружность, точки касания которой служат вершинами треугольника A₁B₁C₁. Найти отношение площади треугольника ABC к площади треугольника A₁B₁C₁ , если даны катеты исходного треугольника АС = 4 см и ВС = 3 см.

2151. Треугольник повернут вокруг центра тяжести на угол 180°. Определить отношение площади общей части исходного и повернутого треугольника к площади исходного треугольника.

2152. Даны стороны треугольника а = 13 см, b = 14 см, с = 15 см. Две из них, а и b, служат касательными к окружности, центр которой лежит на третьей стороне с. Определить площадь круга, ограниченного этой окружностью.

2153. В равнобедренный треугольник с основанием, равным а, вписан квадрат, одна из сторон которого лежит на основании треугольника. Площадь квадрата составляет шестую часть площади треугольника. Определить высоту треугольника и сторону квадрата.

2154. Длины параллельных сторон трапеции равны 20 см и 30 см, а площадь ее равна 400 см 2 . На каком расстоянии от меньшей из параллельных сторон проходит прямая линия, ей параллельная и делящая площадь трапеции на две части, относящиеся, как 2:3 (считая от меньшего, основания)?

2155. Длины двух отрезков, соединяющих середины катетов с вершинами противоположных углов прямоугольного треугольника, равны а и b. Определить площадь треугольника.

2156. Сформулировать какой-нибудь способ построения правильного треугольника, равновеликого данному квадрату.

2157. Высота треугольника, равная 2 см, делит угол треугольника в отношении 2 : 1, а основание треугольника на части, меньшая из которых равна 1 см. Определить площадь этого треугольника.

2158. Площадь треугольника равна S. Каждая сторона треугольника разделена на три части в отношении т : п : т. Определить площадь шестиугольника, вершинами которого служат точки деления.

2159. В прямоугольном треугольнике биссектриса прямого угла отсекает на гипотенузе отрезки длины а и b. Найти площадь квадрата, стороной которого является эта биссектриса.

2160. Около окружности радиуса R =1 см описана равнобочная трапеция, площадь которой равна 5 см 2 , Найти площадь четырехугольника, вершинами которого служат точки касания окружности и трапеции.

Через две смежные вершины квадрата проведена окружность так что

Варианты проверочных работ

Вариант 1

Задание 1.

Площадь прямоугольника равна 81 см 2 , а величина одного из углов, образованных диагоналями, равна 120°. Найдите стороны прямоугольника.

Задание 2.

Найдите площадь круга, описанного около равнобедренного треугольника, если основание треугольника равно 24 см, а боковая сторона равна 13 см.

Задание 3.

Вычислите площадь прямоугольной трапеции, если ее острый угол равен

меньшее основание равно a, a большая боковая сторона равна b.

Задание 4.

Вычислите площадь правильного двенадцатиугольника, вписанного в окружность радиуса 5 см.

Задание 5.

Через вершины произвольного четырехугольника проведены прямые, параллельные диагоналям. Найдите отношение площади параллелограмма, образованного этими прямыми, к площади данного четырехугольника.

Задание 6.

В прямоугольнике ABCD на сторонах АВ и AD выбраны соответственно точки Е и F так, что АЕ : BE = 3 :1, AF : FD = 1 : 2. Найдите отношение ЕО : OD, где О — точка пересечения отрезков DE и CF.

Задание 7.

Окружность называется вневписанной в треугольник, если она касается одной из сторон и продолжений двух других сторон этого треугольника. Найдите радиус вневписанной окружности для равностороннего треугольника со стороной 3 см.

Задание 8.

Через смежные вершины квадрата проведена окружность так, что касательная, проведенная к ней из третьей вершины квадрата, равна удвоенной стороне квадрата. Найдите радиус этой окружности, если длина стороны квадрата равна

Вариант 2

Задание 1.

Внутри острого угла взята, точка А, растояния от которой до сторон и вершины угла относятся как 2 : 11 : 14. Найдите величину этого угла.

Задание 2.

В АВС прямая, параллельная стороне АВ, пересекает сторону ВС в точке М, а сторону АС — в точке N. Площадь MCN в 2 раза больше площади трапеции ABMN. Найдите отношение СМ : МB.

Задание 3.

В трапеции ABCD основание ВС = 3 см, АВ = CD = 3 см. Диагонали трапеции пересекаются под углом 60°. Найдите длину основания AD.

Задание 4.

В АВС известно, что АВ = 40, ВС = 35,

Задание 5.

Окружность радиуса 1 вписана в ААВС, у которого

Эта окружность касается средней линии треугольника, параллельной АС. Найдите длину стороны АС.

Задание 6.

В остроугольном треугольнике

На стороне ВС как на диаметре построена окружность, пересекающая АС в точке Q, а АВ — в точке Р. Найдите отношение площадей APQ и АВС.

Задание 7.

В АВС точка D лежит на стороне АВ, причем

Найдите площадь АВС, если

Задание 8.

В параллелограмме ABCD известны длины сторон АВ = 2, ВС = 4 и диагонали BD = 3. Найдите расстояние между центрами окружностей, вписанных в ABD и ВDС.

Вариант 3

Задание 1.

В АВС

Длины сторон АС и СВ относятся как 5 : 2. Найдите тангенс угла А и длину стороны ВС.

Задание 2.

В прямоугольной трапеции, высота которой равна 4 см, на боковой стороне, не перпендикулярной основанию, как на диаметре построена окружность. Оказалось, что она касается противоположной стороны трапеции. Найдите площадь прямоугольного треугольника, у которого катеты равны основаниям данной трапеции.

Задание 3.

В выпуклом четырехугольнике длины диагоналей равны 1 м и 2 м. Найдите площадь четырехугольника, если известно, что длины отрезков, соединяющих середины его противоположных сторон, равны.

Задание 4.

Сумма длин боковых сторон и высоты трапеции, описанной около окружности, равна 8 см. Найдите максимально возможное значение площади этой трапеции.

Задание 5.

Окружность касается сторон АС и ВС АВС в точках А и В соответственно. На дуге этой окружности, лежащей внутри АBС, взята точка К так, что расстояние от нее до сторон АС и ВС равно 6 и 24 соответственно. Найдите расстояние от точки К до стороны АВ.

Задание 6.

Через центр О вписанной в АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС соответственно в точках М и N. Периметр AMN равен

а отрезок АО втрое больше радиуса вписанной в АВС окружности. Найдите площадь АВС.

Задание 7.

В остроугольном треугольнике ABC биссектриса AD делит пополам отрезок ОН, где О — центр описанной окружности, Н — точка пересечения высот треугольника. Известно, что

Найдите радиус описанной около АВС окружности.

Задание 8.

Равнобедренный треугольник АВС (АВ = ВС) вписан в окружность. Прямая CD, перпендикулярная АВ, пересекает окружность в точке Р. Касательная к окружности, проходящая через точку Р, пересекает прямую АВ в точке Q. Найдите длины отрезков РА и PQ, если АС = 5,

Планиметрические задачи по математике на ЕГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Планиметрические задачи С4.doc

Планиметрические задачи на ЕГЭ (С4)

Халиуллин Асхат Адельзянович, Республика Башкортостан, г. Уфа, почетный работник общего образования Российской Федерации, преподаватель математики Башкирского архитектурно-строительного колледжа .

Обучение решению планиметрических задач является одной из важнейших составляющих практики преподавания математики. Задачи используются как материал, способствующий развитию математического мышления, геометрической интуиции, творческой активности учащихся, формированию умения применять теоретические знания на практике.

Однако, как показывает практика обучения и анализ результатов ЕГЭ выпускников, умение решать планиметрические задачи оставляет желать много лучшего. Задачи С4 по планиметрии вызывают у учащихся наибольшее затруднения. Причиной является сложившаяся и ставшая традиционной практика обучения решению задач по планиметрии по образцу.

Обычно, приступая к решению задачи по планиметрии, учитель предлагает выполнить рисунок аккуратно, с четкими обозначениями, выясняет, что известно и что нужно найти. В процессе выполнения рисунка анализируется условие задачи, устанавливается взаимное расположение отдельных элементов геометрической фигуры и взаимосвязь между этими элементами. Выполнение рисунка требует знания свойств геометрических фигур, умения применять эти свойства на практике.

Если в условии задачи оказывается недостаточно данных для решения, тогда возникает вопрос о выполнении дополнительного построения, которое преобразовало бы условие задачи и направило мысль учащихся в нужном направлении.

Также имеется немало задач, процесс решения которых состоит в последовательном уточнении особенностей рассматриваемой конфигурации с соответствующими переделками и изменениями рисунка, так что окончательный вид рисунок принимает лишь одновременно с окончанием решения.

В данной работе предлагается несколько планиметрических задач, детальный анализ которых позволит убедиться в реальной и существенной пользе проделанной работы.

Проиллюстрируем сказанное выше на наиболее интересных элементарно геометрических задачах на взаимное расположение окружностей и на взаимное расположение прямой и окружности, которые могут быть изучены на факультативных или внеурочных занятиях с наиболее успевающими учащимися с большим интересом, поскольку в школьном преподавании окружность и ее дуги интересны учащимся как представители класса кривых линий.

Решение нижерассматриваемых задач, как и большого класса других задач на вычисление сводится к последовательному рассмотрению и решению ряда прямоугольных треугольников, с которыми проще всего иметь дело. Но в рисунках нижерассматриваемых задач их сразу не видно, поэтому учителю необходимо обучать учащихся умению точно и логично мыслить, видеть, чего в рисунке не достает и какие линии надо провести дополнительно, чтобы можно было создать прямоугольные треугольники и с помощью хорошо известной из школьного курса элементарной геометрии теоремы Пифагора составить уравнения, из которых будут найдены искомые величины.

Поскольку здесь мы имеем дело с окружностями и ее дугами, то является очевидным использование следующих утверждений:

если две окружности касаются внешне или внутренне, то точка касания и центры этих окружностей лежат на одной прямой;

расстояние между центрами двух внешне касающихся окружностей равно сумме радиусов этих окружностей, а расстояние между центрами двух внутренне касающихся окружностей равно разности радиусов большей и меньшей окружностей;

касательная к окружности или ее дуге перпендикулярна к радиусу окружности или ее дуги, проведенному в точку касания.

В процессе решения нижерассматриваемых задач придется много вычислять, что способствует более высокому развитию у учащихся определенных вычислительных навыков. Из всего вышесказанного ясно, что эти задачи окажут учащимся двоякую пользу: во-первых, они получат возможность более глубже понять и прочнее усвоить тему «Окружность», во-вторых, эти задачи разовьют у учащихся умение быстро и безошибочно выполнять различные алгебраические действия.

Задача 1. В квадрате АВСD, сторона которого равна а, из точки А как из центра проведена внутри квадрата дуга через вершины В и D. На стороне DС как на диаметре построена внутри квадрата полуокружность. Найти радиус окружности, касающейся проведенной дуги, полуокружности и одной из сторон квадрата.

Решение.

Поскольку в условии данной задачи конкретно не указано, какой же, именно, сторон квадрата касается искомая окружность, то мы должны рассмотреть три случая, схематически изображенные на рисунке 1(а,б,в).

I.Рассмотрим сначала случай, когда искомая

окружность касается стороне АВ квадрата АВСD (Рис. 1, а). Обозначим радиус этой окружности через х.

Соединим центр окружности О с центром

полуокружности О₁ и с центром дуги А, опустим из центра окружности О перпендикуляры ОМ и О N на противоположные стороны АВ и СD и рассмотрим полученные при этом построении прямоугольные треугольники.

Из прямоугольного треугольника АМО

следует, что неизвестный катет АМ равен

, то есть АМ = или АМ = .

Теперь рассмотрим треугольник ОО₁ N , в котором гипотенуза

OO ₁ = OK ₁ + K ₁ O ₁ = , катет О N = М N – ОМ = а – х и катет О ₁ N = DN – D О ₁ ,

где DN = АМ = _и D О ₁ = поэтому О ₁ N = .

откуда получаем искомый радиус х = OK = .

II. Пусть теперь искомая окружность касается стороне ВС (Рис. 1, б). Обозначим радиус этой окружности через у . Сделаем необходимые дополнительные построения и получаем прямоугольные треугольники АОМ и О₁О N . Из прямоугольного треугольника АОМ по теореме Пифагора найдем катет ОМ.

Он равен ОМ = . Аналогично найдем из прямоугольного треугольника О ₁ О N катет О N = . Подставляя найденные значения величин ОМ и О N в соотношение ВС = ОМ + О N , получаем а = + . Решая это уравнение, находим y = OK = .

II. Искомая окружность касается стороне DC (Рис.1, в).Обозначим радиус этой окружности через z. Опустим из центра О искомой окружности перпендикуляры ОМ и О N соответственно на стороны АВ и CD квадрата АВСD и соединим центр О с центром полуокружности О₁ и с вершиной А квадрата АВСD . Из полученного при этом построении прямоугольного треугольника

ОО ₁ N по теореме Пифагора имеем О ₁ N = . Следовательно, катет АМ прямоугольного треугольника АМО равен

,

откуда и находится искомый радиус z = OK = .

Задача 2. Дан круговой сектор АОВ радиуса R с центральным углом в 90 ○ . На радиусах АО и ОВ этого сектора как на диаметрах построены полуокружности, расположенные внутри данного сектора. Полуокружность с центром О₁ на радиусе ОВ сектора АОВ, радиуса О₁В касается полуокружности, построенной на радиусе АО, и дуги АВ в точке В. Определить радиус окружности, касающейся этих трех полуокружностей.

а) Рис.2 б)

О ₁ О ₂ 2 = О ₁ О 2 + О ₂ О 2 или, так как О ₁ О ₂ = О ₂ К+ О ₁ К = О ₁ В ,

О ₁ О = ОВ — О ₁ В = R — О ₁ В и О ₂ О = , отсюда получаем

.

Следовательно, высота

Теперь мы должны определить стороны прямоугольного треугольника О ₂ О ₄ М . Гипотенуза О ₂ О ₄ = О ₂ К ₂ + К ₂ О ₄ = , катет

О ₂ М = ОО ₂ — ОМ = и катет О ₄ М = .

откуда

З

адача 3. На отрезке АВ, равном R , точка Q – середина; на АQ и на ВQ как на диаметрах по одну сторону от АВ построены полуокружности. С центрами в точках А и В радиусами, равными АВ, проведены дуги до их взаимного пересечения в точке F , находящиеся по ту же сторону от АВ, что и полуокружности. Проведена окружность, которая касается проведенных дуг и полуокружностей. Найти радиус окружности, касающейся окружности, полуокружности, построенной на отрезке ВQ, и дуги В F .

О ₁ О ₂ = О ₁ К ₄ + К ₄ О ₂ =

Поэтому o ткуда

и высота .

Для окончательного решения задачи осталось определить стороны прямоугольного треугольника OPO₂ и подставить в уравнение

катет

Отсюда получаем

После необходимых преобразований находим искомый радиус

Подводя итог, заметим, что ознакомление с предложенными задачами способствует дальнейшему совершенствованию навыков построения и чтения геометрических рисунков, расширению математического кругозора учащихся и поможет им самостоятельно найти решения ряда других, более сложных задач.

Сделаем ещё одно существенное замечание: рассмотрев решение одной – двух задач, изложенное выше, необходимо попытаться решить следующую задачу самостоятельно. Если это не получится, то разобравшись в решении этой задачи, сделать попытку на последующей. Эти попытки не только нужны, но и необходимы, ибо без практики, без тренировки в решении этих задач невозможно научиться решать аналогичные им задачи. Поэтому в заключение работы приведем достаточное количество задач, которых можно предложить для самостоятельного решения ученикам, проявляющим особый интерес к математике.

Задача 1. В квадрате АВСD из точки А как из центра проведена внутри квадрата дуга, проходящая через вершины В и D. На сторонах ВС и СD как на диаметрах построены внутри квадрата полуокружности. Найти радиус окружности, касающейся построенных полуокружностей и дуги ВD, если стороны квадрата равны а.

Ответ. Надо рассмотреть отдельно три случая:

Задача 2. Окружность вписана в квадрат со стороной 1.

Из одной его вершины проведена дуга окружности радиуса 1 до пересечения с другими двумя противоположными вершинами. Проведена окружность, которая касается вписанной окружности и проведенной дуги. Найти радиус окружности, касающейся этой окружности, вписанной окружности и дуги.

Ответ. Два случая:

Задача 3 . Около окружности описан квадрат со стороной а. На двух смежных сторонах этого квадрата построены полуокружности, расположенные внутри квадрата. Найти радиус окружности, касающейся этих двух полуокружностей и окружности.

твет. Четыре случая:

Задача 4. Две окружности радиусов a и b ( a b ) имеют внутреннее касание. Внутри большей окружности проведена касательная к меньшей окружности, перпендикулярная к общему диаметру этих окружностей. Доказать, что отношение радиуса окружности S ₁, касающейся двух данных окружностей

проведенной касательной, к радиусу окружности S ₂, касающейся большей окружности, проведенной каса-

тельной и общего диаметра двух данных окружностей,

равно
Задача 5 . Внутри квадрата со стороной a на двух его смежных сторонах как на диаметрах построены полуокружности. Найти радиус окружности, касающейся этих двух построенных полуокружностей

и одной из сторон данного квадрата.

Ответ: