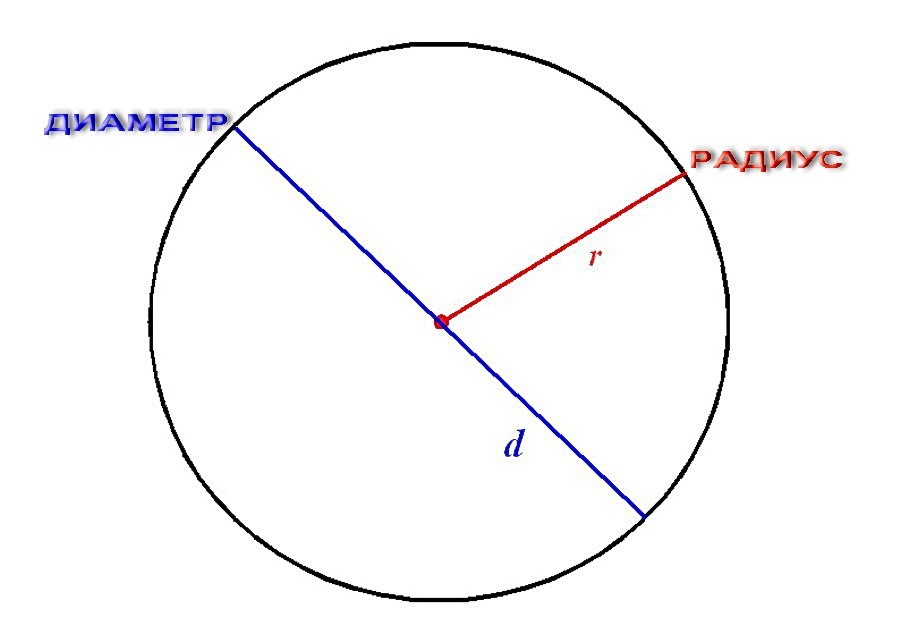
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Видео:Радиус и диаметрСкачать

Диаметр и радиус — что это такое?
В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.
Видео:Длина окружности. Математика 6 класс.Скачать

Понятия радиус и диаметр
Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».
Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.
Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Как использовать эти понятия в жизни
Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.
Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.
В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.
Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.
Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).
Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.
Видео:Окружность и круг, 6 классСкачать

Другие понятия
Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:
- Дуга. Это кривая линия, которая является частью окружности. Ее измеряют в градусах. Сумма всех дуг составляет 360 градусов.
- Хорда. В отличие от кривой дуги это прямой отрезок, который соединяет две точки на окружности. Хорда отличается и диаметра – последний всегда равен двум радиусам и всегда проходит через центральную точку круга. Хорда же может быть длиннее или короче радиуса и никогда не проходит через центральную точку на круге.
- Сектор. Простыми словами, круг – это торт или пирог. Сектор же это треугольный кусок, который вырезается из этого пирога или торта.
- Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.
Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Разница между радиусом и диаметром
Окружность представляет собой кривую линию, которая образована из всех точек, равноудаленных от одной определенной точки, которую называют центром окружности. По-другому можно дать такое определение окружности: кривая, которая замкнута на плоскости, и все точки которой, лежащие в той же плоскости, что и кривая, удалены от центра на одинаковое расстояние. Каждая точка окружности находится от центра окружности на одинаковом расстоянии.
Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

Определение
Радиус — это отрезок прямой, который соединяет каждую точку окружности, которая находится на равном расстоянии от центра окружности, с центром окружности.
Диаметр — это отрезок прямой линии, который соединяет любые две удаленные друг от друга точки окружности и всегда должен проходить через центр этой окружности.
Видео:Радиус Хорда ДиаметрСкачать

Сравнение
Радиусом называют отрезок прямой, который соединяет каждую точку окружности, которая находится на равном расстоянии от центра окружности, с центром окружности. Радиус обозначают буквой R. Он показывает длину этого отрезка. Центр окружности обозначается буквой O.
Диаметром называют отрезок прямой, который всегда должен проходить через центр окружности, и соединять две любые удаленные друг от друга точки окружности. Любой такой отрезок прямой называют диаметром и обозначают буквой D. Длину диаметра также обозначают буквой D.
Пусть точки A, B находятся на самой окружности, тогда отрезки OA, OB — это радиусы этой окружности.
Их длины равны: OB=OA.
BA = OB + OA , так как BA = D, а OA = OB = R , то D = 2R .
Диаметр будет равняться двум радиусам. D = 2R. Соответственно, радиус будет равняться половине диаметра: R = D/2.
💥 Видео
РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Что такое круг окружность радиусСкачать

9 класс, 26 урок, Длина окружностиСкачать

КАК НАЙТИ РАДИУС ОКРУЖНОСТИ ЗНАЯ ДИАМЕТР? КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ ЗНАЯ РАДИУС? ПРИМЕРЫ 6 классСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Окружность. Круг. 5 класс.Скачать

Доли Образование и сравнение долей Математика Моро,Математика 3 класс Моро,МороСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Длина окружности. Площадь круга - математика 6 классСкачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать