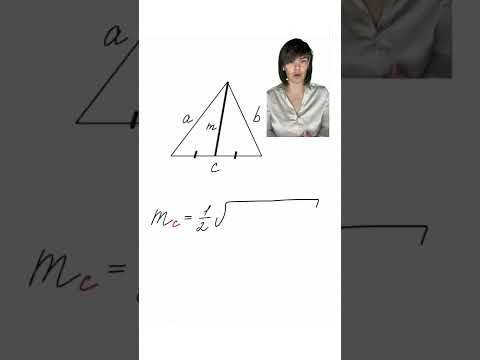Удвоение медианы треугольника задачи (7 видео)

Удвоение медианы

Содержание

Задача по теме удвоение медианы треугольника.
§ 2. Удвоение медианы.. ПРИМЕР 1. Ответ: Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника. Роспись за алгоритм. — презентация
Похожие презентации
Презентация на тему: » § 2. Удвоение медианы.. ПРИМЕР 1. Ответ: Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника. Роспись за алгоритм.» — Транскрипт:
💡 Видео

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Этот урок будет посвящен теме «Удвоение медианы». На этом занятии мы рассмотрим треугольник, в котором проведена медиана. Продлим ее на длину, равную исходному значению медианы и соединим вершины треугольника с полученной удвоенной медианой. В результате мы получим новый четырехугольник, который и рассмотрим.

Видео:Удвоение медианы. Задача.Скачать

Задача по теме удвоение медианы треугольника.

Найдите площадь треугольника, медианы которого равны 12,15 и 21.

Пусть М-точка пересечения медиан AA₁,BB₁,СС_1.

Выполним дополнительные построения: а) удвоение медианы MB₁ треугольника АМС:

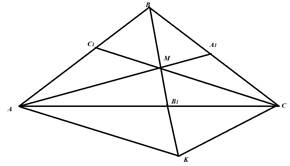
б) Отрезки АК и СК

Далее рассмотрим треугольник АМСК:

B₁K=MB₁, AB₁=CB₁ (т.к. ВB₁-медиана). Таким образом, в четырехугольнике диагонали делятся пополам, а значит, этот четырехугольник параллелограмм (по признаку параллелограмма). Следовательно СК=АМ= АА_1. Медиана треугольника пересекается и точкой пересечения делится в отношении 2:1.

В ΔСМК: СК= АА₁; СМ= СС₁; MK=2MB₁=2*( BB₁)= BB₁

Построим треугольник PQL, таким образом, что его стороны будут равны данным медианам. PQ=BB₁, QL= АА₁, PL= СС₁.

Получаем треугольник, в котором не выполняется теорема Пифагора, так как 21 2 >15 2 +12 2 , то есть PL 2 >QL 2 +PQ 2 . Более того, это означает, что ÐPQL-тупой. Найдем площадь треугольника PQL по формуле Герона, где, а=12, b=15, с=21.

p= = = =24

S_PQL= = =

Рассмотрим треугольники СМК и PQL, они подобны, т.к.

= = ;

= = ; = = ;

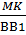
Отсюда следует, что k= , следовательно, отношение площадей треугольников СМК и PQL равняется k 2 = .

S_ΔCMK= * S_ΔPQL= *36

Две фигуры называются равновеликими, если они имеют одинаковую площадь.

Рассмотри ΔCMK: CB₁-медиана (по определению), следовательно, S_ΔCMB₁= S_CMK= *16 .

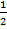
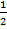
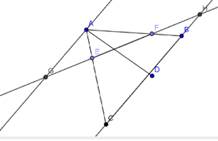
Медианы разбили наш треугольник на 6 частей, отметим это на чертеже. Чтобы найти площадь треугольника АВС достаточно взять одну часть и умножить на шесть.

Значит, S_ΔABC=6* S_ΔCMB₁=6* .=48

Ответ: S_ΔABC= 48

Заметим, что данную задачу решить лишь алгебраическим путем было бы если не невозможно, то значительно труднее. Применяя дополнительные построения, мы сумели пошагово решить данную задачу.

Если в треугольнике заданы некоторая трасверсаль (отрезок прямой, проведенной через его вершину, заключенный внутри треугольника) и отрезок с концами на двух сторонах треугольника, пересекающий эту трансверсаль и не параллельный третьей стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит трансверсаль.

Задача

В треугольнике ABC проведена высота ВВ₁ и медиана СС₁. Известно, что их точка пересечения О отстоит от стороны АС на расстоянии 1см. Определите АВ, если ВВ₁ =6; СС₁ = 5.

Дано: АВС, ВВ₁ – высота, СС₁ –медиана, ВВ₁ СС₁ = О, ОВ₁ = 1см, ВВ₁ = 6см,

Решение:

Построим С₁С₂║АС ВВ₂ = В₂В₁ т.к. является С₁С₂ средней линией треугольника ABC и делит пополам любой отрезок соединяющий вершину B с точкой

стороны AC.

ОВ₁С ОВ₂С₁ = CC₁ = 3х = 5 х = ; ∆ОВ₁С: В₁С = = ; АВ₁ = 4В₁С = 4 =

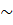
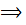
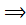
∆АВВ₁: АВ = = =

Ответ:

Если в треугольнике заданы отрезок с концами на двух сторонах треугольника и высота (медиана, биссектриса), пересекающий эту высоту (медиану, биссектрису), и не параллельный третьей стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит высота (медиана, биссектриса).

Задача

Точки R и L лежат на боковых сторонах АВ и ВС равнобедренного треугольника АВС так, что АR = АВ; CL = BC. Определите, в каком отношении отрезок RL делит высоту ВВ₁ треугольника АВС.

Дано: АВС, АВ = ВС, R АВ, L BC, АR = АВ; CL = BC.

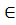
Найти:

Решение:

Построим ВR₁ АС ,продолжим RL до пересечения с BR₁ и АС в точках R₁ и L₁ ∆ВRR₁ ∆АRL₁ = = == = ;

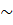
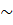
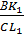
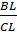
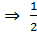
∆BLK₁ ∆CLL₁ = = = 3;

AL₁ = 3СL₁ AL₁ = 6CL₁ АС = 5CL₁

B₁C = AC = CL₁;

B₁L₁ = CL₁ + CL₁ = CL₁ = AL₁ ∆BGR₁ ∆В₁GL₁ = = = .

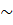
Ответ: =

2. Стандартное дополнительное построение в задачах на трапецию: проводим либо два перпендикуляра к основанию и получаем прямоугольник и два прямоугольных треугольника, либо проводим отрезок, параллельно боковой стороне, и получаем параллелограмм и произвольный треугольник, либо проводим через середину меньшего основания прямые, параллельные боковым сторонам, либо продлеваем боковые стороны до пересечения. Если же в условии задачи говорится о диагоналях трапеции, то стандартным будет дополнительное построение, состоящее в проведении через одну из ее вершин прямой, параллельной диагонали.

Возьмем геометрическую фигуру — трапеция, и постараемся выделить наиболее часто используемые дополнительные построения при решении задач.

1) Опускание высот из концов одного основания на другое основание;

2) Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину;

3) Проведение через середину меньшего основания прямых, параллельных боковым сторонам;

4) Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину;

5) Продолжение боковых сторон до пересечения.
Дополнительное построение позволяет разбить трапецию на прямоугольник (стороны которого – одно из оснований и высота трапеций ) и 2 прямоугольных треугольника ( в которых один из катетов — высота трапеции, а гипотенузы — боковые стороны трапеции). Это часто позволяет произвести нужные вычисления.

Дополнительные построения встречаются по всему курсу планиметрии с 7 по 9 классы.

Задача

В равнобедренном треугольнике с боковой стороной 8 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 6 см.

Дано: ΔABC, AB= BC 8 см, BE= EC, AE= 6см.

Найти: AC .

Решение. 1) достроим _ΔABC до параллелограмма ABCD, центром которого является точка E .

2) АЕ=6, AD=2AE=12, AC=x.

3) AD 2 +BC 2 =2(AB 2 +AC 2 )=12 2 +8 2 =2(8 2 +x 2 )→x=2

Ответ: 2 см.

В треугольнике ABC на стороне AC взята точка M, такая, что AM= , а на стороне BC– точка K, такая, что BK= . В каком отношении отрезок BM делит отрезок AK?

Дано: ΔABC, AM= , BK= .

Найти: .

Решение: проведем через точку А прямую, параллельную ВС, и обозначим через L точку её пересечения с прямой ВМ. Пусть ВК=ɑ, тогда ВС=3ɑ.

_ΔAML ∼ _ΔCMB, поэтому , отсюда , AL= 2ɑ. Далее из подобия треугольников LAN и BKN найдем

Ответ:

При решении геометрических задач традиционные методы иногда приводят к громоздким решениям, поэтому важной составной частью геометрических методов решения являются дополнительные построения.

Дополнительные построения используются для:

· появления новых фигур и возможность использовать формулы, свойства и теоремы, связанные с ними;

· появление подобных или равновеликих фигур;

· появление пропорциональных отрезков.

Чтобы построить геометрический чертеж учащийся должен уметь оперировать пространственными образами во внутреннем плане. Однако этот опыт является необходимым, но не достаточным залогом успешности деятельности по построению чертежей в незнакомых ситуациях. Важным компонентом формирования геометрического мышления является специальная организация диалога между внешним и внутренним планами. В зависимости от уровня притязаний учащегося и индивидуальных особенностей его пространственного мышления зависит выбор методов и средств построения. Сформулированные требования к геометрическому опыту ученика при решении задач «с карандашом и бумагой» не утрачивают своей значимости и при использовании мультимедийных технологий. Выделим основные требования к использованию дополнительных построений. Итак:

1. Только при наличии в памяти учащегося базового набора образов геометрических тел и их конфигураций виртуальные компьютерные модели станут для него вполне аналогичны исходным, а значит, их использование позволит достигать ожидаемых трехмерных эффектов.

2. Применение готовых виртуальных интерактивных моделей, позволяющих увидеть геометрическую конфигурацию с разных точек зрения, дает возможность значительно расширить виды упражнений с готовыми наглядными демонстрациями и минимизировать наборы используемых материальных моделей.

3. Регулярное применение на уроках геометрии интерактивной доски, заранее заготовленных чертежей, различных виртуальных моделей фигур и их комбинаций позволяет учителю более интенсивно использовать время урока, а учащимся значительно облегчает процесс решения знакомых и видоизмененных задач. Вместе с тем чрезмерное увлечение готовыми электронными ресурсами тоже может отрицательно сказаться на формировании пространственного мышления учащихся. Избежать этого помогут существующие стереоконструкторы, позволяющие ученику не только самостоятельно выполнять необходимые чертежи и мультипликации, но и управлять их содержанием, формой, размерами и цветом. Поэтому эти инструментальные среды дают возможность сместить акценты в геометрической подготовке школьников в сторону усиления ее моделирующего аспекта, открывают принципиально новые возможности анализа и самостоятельного эмпирического обобщения геометрического материала.

4. Продуктивная и осознанная работа со стереоконструктором не освобождает ученика от знания основ теории изображений. Напротив, уровень решаемых учащимся задач во многом определяется уровнем его теоретической подготовки.

Сказанное еще раз подчеркивает уникальность школьной геометрии как учебного предмета и таящийся в ее изучении развивающий потенциал. Пространственное видение, методы геометрических построений помогают человеку размышлять и думать глубже. Отсюда также следует, что при обучении геометрии должно уделяться гораздо больше внимания работе с чертежами, чем это делается традиционно.

Данная тема курсовой работы, помогла мне изучить глубже психологию школьника, а так же позволила понять, трудности и ошибки многих преподавателей в школе.

Список используемой литературы

Педагогическое мастерство: материалы V Mеждунар. науч. конф. (г. Москва, ноябрь 2014 г.). – М.: Буки-Веди, 2014. – vi, 130 с.

Веккер Л. М. Психика и реальность: единая теория психических процессов. М.: Смысл; Per Se, 2000. 685 с.

Гальперин П. Я. Психология как объективная наука. М.: Ин-т практической психологии; Воронеж: НПО «МОДЭК», 1998. 480 с.

Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989. – 252с.

Полонский В.Б. и др. Учимся решать задачи по геометрии. В.Б. Полонский, Е.М. Рябинович, М.С. Якир. – Киев.,1996. – 253 с.

Васильев А. Александр Попов и Гульельмо Маркони //Квант. — 2000. — № 6. — С. 18-19.

Журнал теоретических и прикладных исследований. — Екатеринбург: Уральское отделение Российской академии образования. — 159 с. — ISSN 1994-85-81.

Видео:Геометрия 8 Класс Урок 4 Удвоение медианыСкачать

§ 2. Удвоение медианы.. ПРИМЕР 1. Ответ: Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника. Роспись за алгоритм. — презентация

Презентация была опубликована 8 лет назад пользователемЮлия Лашманова

Презентация на тему: » § 2. Удвоение медианы.. ПРИМЕР 1. Ответ: Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника. Роспись за алгоритм.» — Транскрипт:

1 § 2. Удвоение медианы.

3 Ответ: Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника. Роспись за алгоритм решения Роспись за запись решения на доске Всегда приятно, когда треугольник оказывается прямоугольным

4 Роспись за алгоритм решения Оригинальный способ решения : дополнительное построение — удвоение медианы треугольника.

5 ПРИМЕР 4. Площадь треугольника ABC равна S. Найдите площадь треугольника, стороны которого равны медианам треугольника ABC Уникальный ход. 1. Медианы точкой пересечения делятся 2:1, считая от вершины Известные факты… 2. Медианы разбивают треугольник на 6 равновеликих треугольника Ответ:

6 ПРИМЕР 5. Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции. Ответ: Уникальный ход. 1. Заменим трапецию на равновеликий треугольник 2. Удвоение медианы треугольника Всегда приятно, когда треугольник оказывается прямоугольным

7 9 подготовительных задач 2.1. Медиана AM треугольника ABC равна т и образует со сторонами АВ и АС углы α и β соответственно. Найдите эти стороны В треугольнике ABC известно, что BD медиана,, a DBC = 90°. Найдите угол ABD Найдите площадь треугольника, если две стороны его соответственно равны 27 и 29, а медиана, проведённая к третьей, равна 26. Балл за решение каждой задачи

8 9 подготовительных задач 2.4. Стороны треугольника равны 11, 13 и 12. Найдите медиану, проведённую к большей стороне В треугольнике две стороны равны 11 и 23, а медиана, проведённая к третьей, равна 10. Найдите третью сторону В равнобедренном треугольнике с боковой стороной, равной 4, проведена медиана к боковой стороне. Найдите основание треугольника, если медиана равна 3. Балл за решение каждой задачи

9 9 подготовительных задач Балл за решение каждой задачи