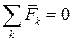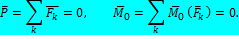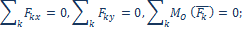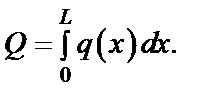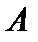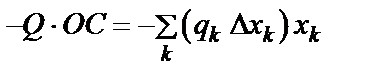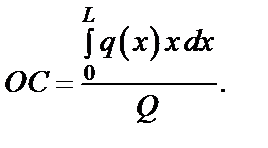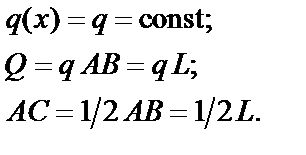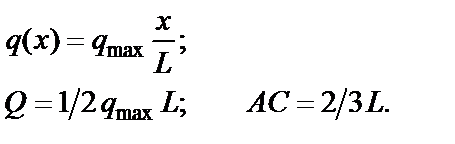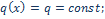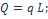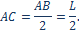Разберем еще один вопрос — в чем состоит разница понятий главного вектора системы сил и равнодействующей? Главным вектором называют силу, равную векторной сумме всех действующих в системе сил:
В отличие от равнодействующей, величину которой находят (когда она существует) по той же формуле, при определении главного вектора не конкретизируется точка приложения этой силы. Равнодействующая полностью заменяет собой систему сил, она эквивалентна ей. Равнодействующая не всегда существует. Простейший пример системы сил не имеющей равнодействующей — это пара сил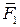 
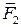
и 
, линии действия которых параллельны, величины равны, направления — противоположны.
В случае неуравновешенной сходящейся системы сил равнодействующая существует. Она равна по величине главному вектору и приложена в точке пересечения линий их действия
Дата добавления: 2015-08-08 ; просмотров: 5998 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать
Сравнение понятий «главный вектор» и «равнодействующая».
В чем состоит разница понятий «главный вектор системы сил» и «равнодействующая системы сил»?
Главным вектором системы сил называют силу, равную векторной сумме сил, образующих систему (в связи, с чем главный вектор может быть определен для любой системы сил):
.
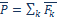
Главный вектор системы сил может заменить любую систему сил только вместе с главным моментом.
Как следует из определения равнодействующей — это одна сила заменяющая систему сил (эквивалентная системе сил). Равнодействующая существует не всегда. Простейшим примером системы сил, не имеющей равнодействующей, может быть пара сил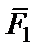 
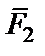
и 
. В случае неуравновешенной системы сходящихся в точке сил, равнодействующая существует, и в таком случае равна главному вектору и приложена в точке пересечения линий действия сил, образующих указанную систему.
Частные случаи приведения системы сил к центру.Возможные случаи приведения системы сил определены комбинациями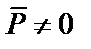 
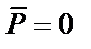
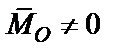
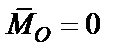
или 
и 
или 
.
Практический интерес для определения условий равновесия представляет частный случай, когда главный вектор и главный момент равны нулю. В этом случае система сил уравновешена:
Другие частные случаи приведения систем сил сведены в таблицу.
| 1. P ≠ 0; MО = 0 | Равнодействующая |
| 2. P = 0; MО ≠ 0 | Пара сил |
| 3. P ≠ 0; MО ≠ 0, α = π/2 | Равнодействующая |
| 5. P ≠ 0; MО ≠ 0, α ≠ π/2 | Динама |
Условия равновесия плоской произвольной системы сил.Совместим одну из координатных плоскостей (например, xOy) с плоскостью действия сил. Тогда условия равновесия запишутся в виде трёх уравнений:
Условия равновесия произвольной плоской системы сил в таком виде называют основной формой условий.
1.5. Распределенные силы
Силы, приложенные в точке, называют сосредоточенными. В действительности взаимодействие тел может происходить по некоторой линии или поверхности либо объёму. Примером поверхностных сил является давление воды на подводную часть корабля, примером объёмных служат силы тяжести, распределенные по объёму тела (часто, для удобства распределённые силы заменяют равнодействующей, приложенной в центре тяжести).
Распределённые силы характеризуются интенсивностью и направлением действия. Интенсивностью распределённой нагрузки называется величина силы, приходящаяся на единицу объёма, площади или длины линии.
Силы принимаются распределёнными по линии в том случае, когда размерами тела в поперечном сечении можно пренебречь по сравнению с его длиной. Такие тела называются стержнями или балками. Распределёнными, обычно, бывают параллельные или сходящиеся силы, однако распределёнными могут быть и пары сил.
Рассмотрим вопросы замены распределённых сил сосредоточенными. Пусть силы распределены по отрезку АВ длиной L (рис. 1.15). Разобьём отрезок AB на элементарные участки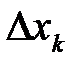 
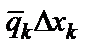
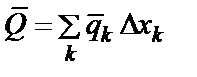
. На каждый из них действует сила, равная 
, так как из-за малости участка интенсивность в его пределах можно считать постоянной. Суммируя элементарные силы, найдём равнодействующую. Величина её равна главному вектору:
.
При устремлении к нулю элементарной длины Dxk сумма сил перейдёт в интеграл
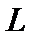
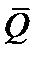
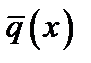
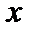
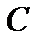
Рис. 1.15. Распределенная нагрузка
Точка приложения равнодействующей силы определяется с помощью теоремы Вариньона:
или при предельном переходе
,
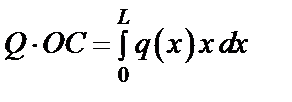
Частные случаи распределенных нагрузок.Случай распределения с постоянной интенсивностью (равномерно распределенные нагрузки) приведен на рис. 1.16:
Рис. 1.16. Распределение с постоянной интенсивностью
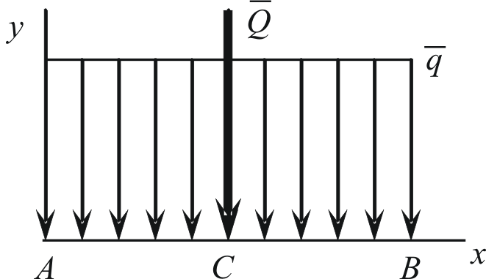
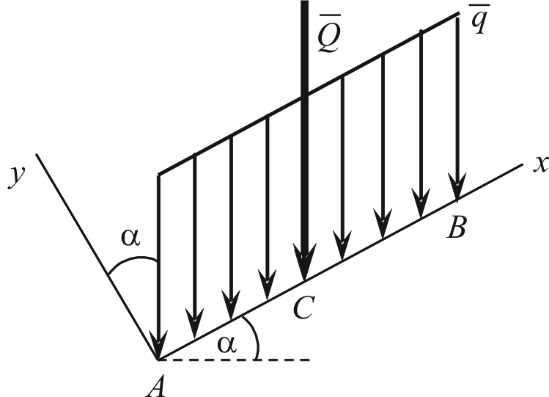
Распределение с линейно изменяющейся интенсивностью (рис. 1. 17 а), если AB = L:
 |
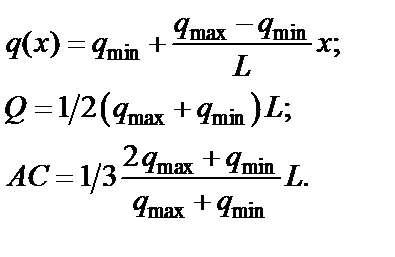| а) | б) |
 |  |
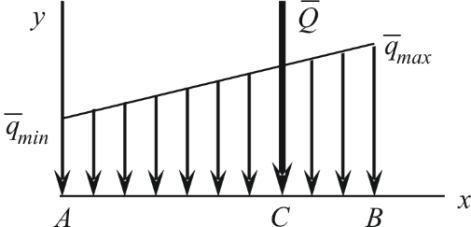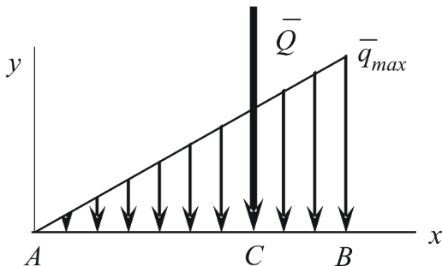Рис. 1.17. Распределение с линейно изменяющейся интенсивностью (а)
и с интенсивностью, изменяющейся по закону треугольника (б)
Если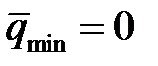 
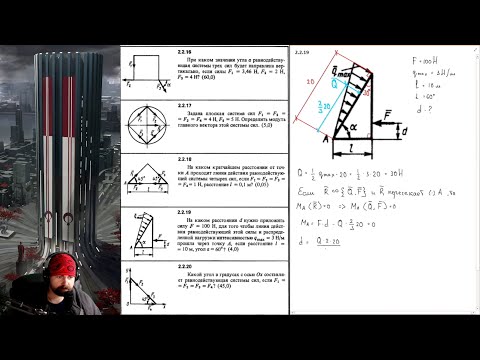
(рис. 1.17 б), получим треугольное распределение:
Рис. 1.18. Распределенная нагрузка, заданная под углом
При распределённой нагрузке, заданной под углом α, имеем распределение с постоянной интенсивностью (рис.1. 18):
Статически определимые и статически неопределимые задачи.Число независимых уравнений равновесия определяется видом системы внешних сил, приложенных к объекту равновесия. Например, для произвольной плоской системы сил таких уравнений три, а для произвольной пространственной — шесть.
Неизвестные в уравнения равновесия представлены реакциями внешних связей, в некоторых случаях неизвестными активными силами и (или) моментами. В том случае, когда число неизвестных не превышает количество уравнений равновесия задачу называют статически определимой. Если число неизвестных больше количества уравнений равновесия – статически неопределимой задачей.
Методы статики применимы только к статически определенным системам. Решение статически неопределимых задач возможно при учете деформаций тел методами сопротивления материалов.
2. Методика решения задач
на равновесие произвольной системы сил
Любая задача статики изучаемого курса может быть решена в указанной последовательности.
1. Выделить объект равновесия (тело (элемент) или систему тел, равновесие которых будем рассматривать) и изобразить его как свободное тело (применение аксиомы освобождения от связей).
2. Приложить к объекту равновесия активную нагрузку (силы, пары сил) в соответствии с условием задачи.
3. Вместо отброшенных связей приложить к объекту равновесия реакции этих связей.
4. Выполнить анализ полученной системы сил (активных и реакций внешних связей), ответив на вопросы:
— Получена система сил, лежащих в одной плоскости или пространственная?
— Каково взаимное расположение линий действия сил? (Получена система произвольно расположенных сил или система параллельных сил или сил, сходящихся в точке?)
Следовательно, сколько независимых уравнений равновесия может быть составлено?
5. Сравнить число неизвестных (реакций связей) и количество независимых уравнений равновесия. Выяснить, является задача статически определённой или нет.
6. В случае статически определенной системы составить уравнения равновесия и решить их.
Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать
Please wait.
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать
We are checking your browser. megamozg.com
Видео:Момент силы относительно точки и осиСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d409cad9e9d16db • Your IP : 85.95.179.65 • Performance & security by Cloudflare
📹 Видео
Физика | Ликбез по векторамСкачать
§4.3. Главный вектор и главный момент сил инерцииСкачать
1 Решение задачи графическим и аналитическим методомСкачать
Система сходящихся силСкачать
Приведение системы сил к простейшему видуСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Основная теорема статикиСкачать
Графический способ определения равнодействующейСкачать
Геометрический способ определения равнодействующей силыСкачать
Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать
Приведение системы сил к простейшему видуСкачать
5.3. Главный момент произвольной пространственной системы силСкачать
Теорема Вариньона о моменте равнодействующейСкачать
Урок 82. Равнодействующая параллельных сил. Пара силСкачать
