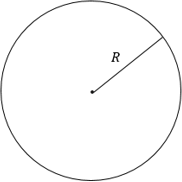
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Видео:Окружность и круг, 6 классСкачать

Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
| πr 2 n |
| 360 |
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
| S = | sr | , |
| 2 |
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Видео:Окружность. 7 класс.Скачать

Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
| S = | r | (s — BC), |
| 2 |
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
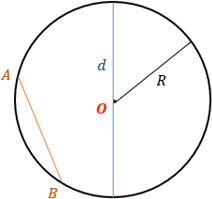
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
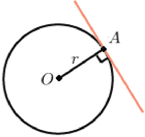
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
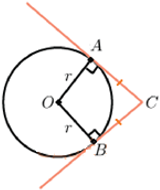
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

51. Планиметрия  Читать 0 мин.
Читать 0 мин.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

51.364. Окружнoсть
Окружность ― множество всех точек плоскости, равноудаленных от данной точки на плоскости (то есть замкнутая линия).
Круг ― часть плоскости, ограниченная окружностью (то есть площадь).
Элементы окружности:
Центр окружности ― точка O.
Радиус окружности (r) ― отрезок, соединяющий точку окружности с центром. Все радиусы одной окружности равны.
Диаметр (d) ― хорда, проходящая через центр окружности. Диаметр равен двум радиусам.
Хорда (AB) ― отрезок, соединяющий любые две точки окружности.
Площадь круга и длина окружности:
Дуга и сектор:
Дуга окружности — участок окружности между двумя точками на ней.
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.
Длина дуги окружности:
Площадь сектора:
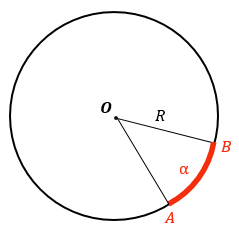
Чтобы найти длину дуги АВ, нужно понять, какую часть она занимает от всей окружности. Это можно сделать через градусную меру дуги (угол между отрезками ОА и ОB).
Если окружности — R, а градусная мера дуги АВ — α, то длина всей окружности = 2ℼR, а дуга занимает от всей окружности α/360°.
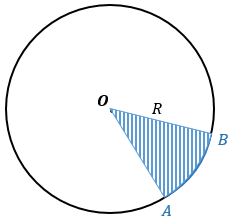
Чтобы найти площадь сектора ОАВ, нужно понять, какую часть он занимает от всего круга, что можно сделать через градусную меру дуги АВ.
Если окружности — R, а градусная мера дуги АВ — α, то площадь всего круга = πR 2 , а дуга занимает от всей окружности α/360°.
Касательная к окружности:
Касательная ― прямая, имеющая с окружностью ровно одну общую точку.
СВОЙСТВА КАСАТЕЛЬНОЙ:
Центральные и вписанные углы:
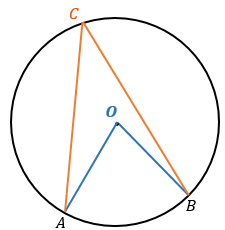
Вписанный угол (ACB) ― угол, вершина которого лежит на окружности, а стороны являются ее хордами
Центральный угол (AOB) ― угол, образованный двумя радиусами:
1. Измеряется половиной дуги, на которую он опирается;
2. Вписанные углы, опирающиеся на одну и ту же дугу, равны;
3. Вписанный угол, опирающийся на диаметр — прямой.
1. Измеряется дугой, на которую опирается;
2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
📽️ Видео
Круг. Окружность | Математика 3 класс #21 | ИнфоурокСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Окружность, ее элементы и кругСкачать

Геометрия 9 класс (Урок№24 - Площадь круга. Площадь кругового сектора.)Скачать

Фифа 24 Часа в Деревне Челлендж !Скачать

Окружность круг хорда диаметр радиус дуга сектор сегментСкачать

Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Урок по математике 5 класс на тему «Окружность и круг», учитель Колебошин С.В.Скачать

Масштаб. 6 класс.Скачать

Радианная мера угла. 9 класс.Скачать

Геометрия. 7 класс. Определения. Часть 3. Окружность.Скачать

Площадь кругаСкачать

Математика 6 класс Круговые ДиаграммыСкачать

Окружность. Урок №1Скачать
















 Читать 0 мин.
Читать 0 мин.