Боковые треугольники четырехугольной пирамиды

Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .

Видео:Боковые ребра треугольной пирамиды взаимно перпендикулярныСкачать

Что такое пирамида в общем случае?

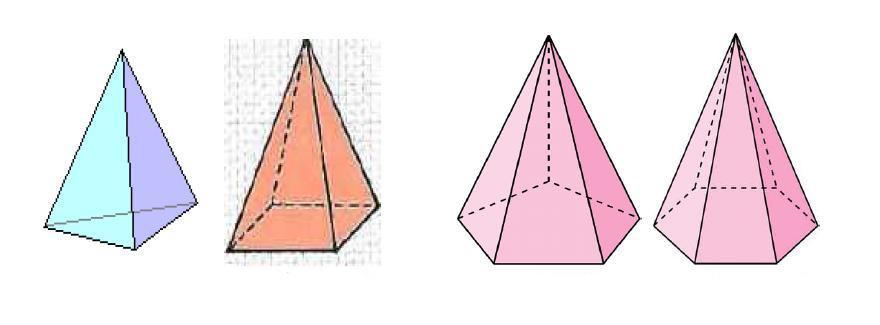
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

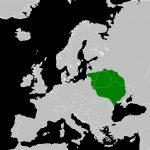
Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

• в основании должен находиться правильный многоугольник;
• боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Видео:Правильная четырехугольная пирамида. Угол между боковой гранью и основанием. Найти ребро основанияСкачать

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

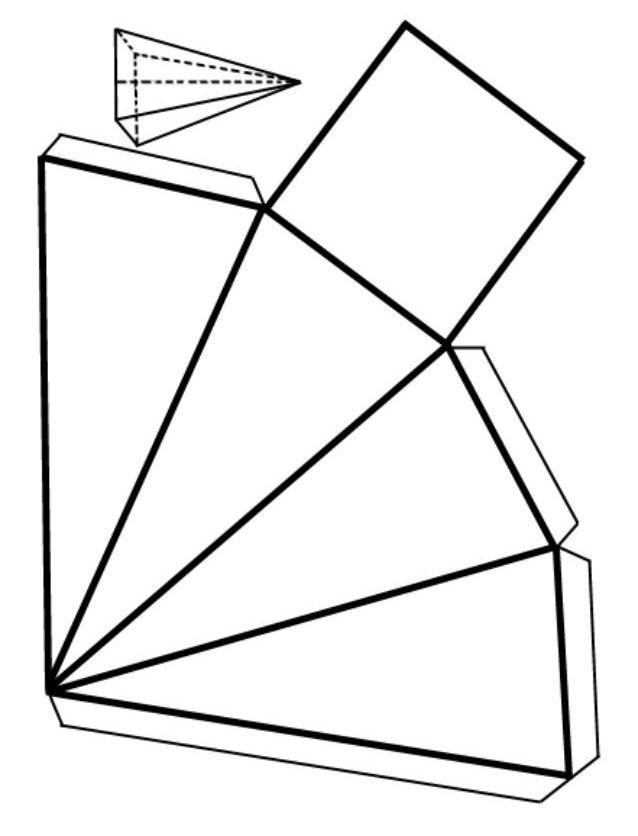
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Видео:Найти площадь боковой поверхности правильной треугольной пирамидыСкачать

Свойства правильной усеченной четырехугольной пирамиды

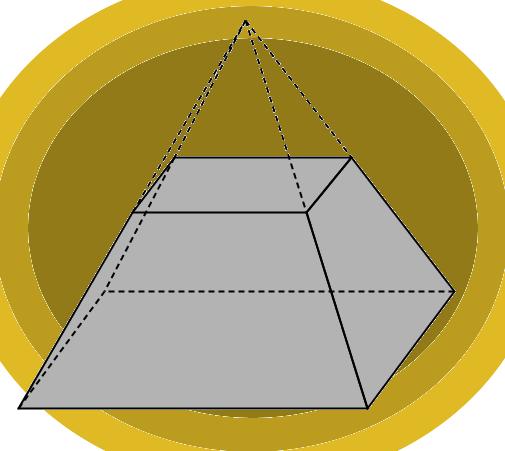
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Здесь h — расстояние между основаниями фигуры, So1, So2 — площади нижнего и верхнего оснований.

Видео:Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Формулы и свойства правильной четырехугольной пирамиды

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Что собой представляет пирамида

Под пирамидой понимают геометрическую фигуру пространственную, которая получается в результате соединения всех углов многоугольника с одной точкой пространства. Рисунок ниже демонстрирует расположение линий (ребер) для четырехугольной и пятиугольной пирамид.

Многоугольная грань фигуры называется ее основанием. Точка, где все треугольные грани соединяются, называется вершиной. Для определения высоты пирамиды отмеченные элементы являются важными.

Видео:11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Правильная треугольная пирамида.

Правильная треугольная пирамида – это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.

Видео:№258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.Скачать

Элементы правильной пирамиды

• Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
• Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
• Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
• Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
• Диагональное сечение пирамиды – это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
• Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)

Если в основании правильной пирамиды лежит треугольник, четырехугольник и т.д. то она называется правильной треугольной , четырехугольной и т.д.

Треугольная пирамида есть четырехгранник — тетраэдр .

Видео:#121. Задание 8: четырехугольная пирамидаСкачать

Высота фигуры

Высотой пирамиды называется перпендикуляр, который из ее вершины опущен на плоскость основания. Важно понимать, что из каждой вершины, принадлежащей основанию фигуры, тоже можно провести перпендикуляр к соответствующей треугольной грани, однако он высотой не будет являться. Высота пирамиды – это единственный перпендикуляр, который является одной из важных ее линейных характеристик.

Каждому школьнику известно, что любая плоская фигура обладает геометрическим центром (в физике ему соответствует центр масс). Например, геометрический центр для произвольного треугольника определяется точкой пересечения его медиан, для параллелограмма – точкой пересечения диагоналей. Если высота пирамиды пересекает ее основание в геометрическом центре, то фигура называется прямой. Пирамида прямая, имеющая в основании многоугольник с одинаковыми сторонами и углами, называется правильной.

Рисунок выше показывает, чем отличается неправильная пирамида от правильной. Видно, что высота неправильной фигуры лежит за пределами ее основания, в то время как у правильной шестиугольной пирамиды высота находится внутри фигуры, пересекая ее основание в центре геометрическом.

Важными свойствами всех правильных пирамид являются следующие:

• все боковые грани представляют собой равнобедренные треугольники и равны друг другу;
• длины боковых ребер и апофем являются одинаковыми.

Видео:В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью...Скачать

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

• в основании должен находиться правильный многоугольник;
• боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:№259. В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковойСкачать

Объем пирамиды

Формула для нахождения объема пирамиды через площадь основания и высоту:

<V= dfrac S h> , где S — площадь основания, h — высота пирамиды.

Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Видео:Развертка пирамидыСкачать

Правильная пирамида с треугольным основанием

Фигура, которая получена с использованием произвольного треугольника и точки в пространстве, будет неправильной наклонной пирамидой в общем случае. Теперь представим, что исходный треугольник имеет одинаковые стороны, а точка пространства расположена точно над его геометрическим центром на расстоянии h от плоскости треугольника. Построенная с использованием этих исходных данных пирамида будет правильной.

Очевидно, что число ребер, сторон и вершин у правильной треугольной пирамиды будет таким же, как у пирамиды, построенной из произвольного треугольника.

Однако правильная фигура обладает некоторыми отличительными чертами:

• ее высота, проведенная из вершины, точно пересечет основание в геометрическом центре (точка пересечения медиан);
• боковая поверхность такой пирамиды образована тремя одинаковыми треугольниками, которые являются равнобедренными или равносторонними.

Правильная треугольная пирамида является не только чисто теоретическим геометрическим объектом. Некоторые структуры в природе имеют ее форму, например кристаллическая решетка алмаза, где атом углерода соединен с четырьмя такими же атомами ковалентными связями, или молекула метана, где вершины пирамиды образованы атомами водорода.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Формулы для высоты правильной пирамиды

Существует четыре основных линейных характеристики для любой пирамиды правильной:

• сторона основания;
• боковое ребро;
• апофема боковой грани;
• высота фигуры.

Все они связаны математически друг с другом. Обозначим длину стороны основания символом a, высоту — h, апофему — hb и ребро — b. Формулы, которые эти величины связывают, имеют индивидуальный вид для соответствующей n-угольной пирамиды. Например, для правильной пирамиды четырехугольной высоту можно определить по формулам:

Эти формулы следуют из теоремы Пифагора при рассмотрении соответствующих прямоугольных треугольников внутри пирамиды.

Если рассматривается фигура с треугольным основанием, тогда справедливы следующие формулы для высоты правильной пирамиды:

Видео:Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. РЕШЕНИЕ!Скачать

Пирамида

Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Видео:В правильной четырехугольной пирамиде боковое ребро равно 22Скачать

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Видео:ЕГЭ Задание 14 Правильная четырехугольная пирамидаСкачать

Виды пирамид

Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Видео:Найти объем правильной треугольной пирамидыСкачать

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

🎬 Видео

Площадь боковой поверхности треугольной пирамиды. #shortsСкачать