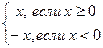Блок схема вычисления площади окружности

Линейными являются алгоритмы отпирания дверей, заваривания чая, приготовление одного бутерброда. Линейный алгоритм применяется при вычислении арифметических выражений, если в нем используются только сложение и вычитание.

алг (заголовок с указанием типа величин)

дано (перечисляются аргументы)

надо (перечисляются результаты)

конПример: Напишите алгоритм открывания замка.

алг открой замок
нач
достань ключ
вставь в замочную скважину
поверни налево два раза
(замок открыт)

Какое из приведенных описаний удовлетворяет требованиям описания алгоритма на алгоритмическом языке (что пропущено в каждом случае). Укажите под какой буквой дана правильная запись.

Простейшие линейные программы.

Программа — набор инструкций для вычислительных машин и устройств. В языке программирования Бейсик используют следующие операторы:

REM — записываются комментарии к программе. Компьютер на этот оператор внимание не обращает.

PRINT (?) -позволяет выводить результаты на экран, выражение заключённое в кавычки выводится без изменения.

INPUT — позволяет вводить данные в результате выполнения программы, встретив оператор INPUT компьютер на экране печатает знак вопроса и ждет ввода данных.

END — указывает на завершение программы.

Для начала строчки программы можно нумеровать в порядке возрастания.

Задача: Записать алгоритм, блок — схему и программу для нахождения площади круга и длины окружности радиуса R. алг вычисление площади круга и длины окружности (вещ R,вещ S, C)

10 REM вычисление площади круга и длины окружности

20 INPUT «Введи радиус круга, R и П«; R, П

1. Определить среднюю экономию горюче-смазочных материалов в автобусном парке за месяц, если известна средняя экономия в день по бензину, дизельному топливу, солидолу.

10 REM ЭКОНОМИЯ ГСМ

20 INPUT «ВВЕДИ бензин-В, диз.топ.-D, солидол-С, кол-во дней -N»; B, D, C, N

2. Изготовление изделия состоит из нескольких этапов. На первый этап уходит 16 мин, на 2-ой 23 мин, на 3-ий 73 мин, на 4-ый — 30 мин, на 5-ый — 8 мин. Сколько полных циклов изготовления детали можно выполнить за сутки.10 REM кол-во циклов

20 INPUT «ВВЕДИ T1, T2, T3, T4, T5»; T1, T2, T3, T4, T5

30 T=T1 + T2 + T3 + T4 + T5

50 ? «за сутки»; N; «циклов»

3. Составьте программу вычисления подоходного налога от заработной платы (13% от общей суммы)10 REM подоходный налог

40 ? «подоходный налог составляет»; N; «руб»

Задача. Вычислить площадь круга.

Дано: R, радиус круга.

Требуется: S, площадь руга.

Запишем алгоритм словесно (на русском языке). То есть запишем последовательность команд, выполнение которых позволит при заданном значении радиуса круга найти его площадь:

Прочесть (получить) значение R. (ВВОД ДАННЫХ)

Присвоить переменной S значение выражения 3,14*R*R. (КОМАНДА ПРИСВАИВАНИЯ)

Записать (вывести) полученное значение S. (ВЫВОД РЕЗУЛЬТАТА)

Короче можно записать так:

Прочесть значение R

Записать значение S

Знак «:=» означает «присвоить». Запись А:=А+2 в программировании она означает команду присваивания. Сначала исполнитель вычисляет значение выражения, стоящего в правой части, а затем полученное значение присваивает переменной, стоящей в левой части. Например, после выполнения команд х:=3; х:=х*5 переменная х примет значение 15.

Графическая форма представления основана на замене типичных алгоритмических команд определенными геометрическими фигурами.

Разветвляющиеся алгоритмы. Команда ветвления.

Существует широкий круг задач, при решении которых необходимо сделать определенный выбор в зависимости от выполнения некоторых условий. Процесс решения таких задач описывается алгоритмом, тип которого определяется как ветвящийся (разветвляющийся). В разветвляющихся алгоритмах принцип линейного автоматического перехода от команды к команде, от действия к действию в порядке естественного следования не является всеобщим, так как иногда возникает необходимость произвольного перехода к предписанию, то есть нарушения линейности переходов. Ветвящиеся алгоритмы допускают два способа представления — графический и словесный.

При графическом представлении алгоритма ветвление (развилка, выбор дальнейших действий) организуется с помощью логического элемента (ромб с записанным внутри условием), имеющего один вход и несколько (в простейшем случае — два) выходов. Назначение логического элемента — проверка заданного условия. В зависимости от выполнения (истинности) или невыполнения (ложности) проверяемого условия возможен выход соответственно на ветвь «Да» или «Нет». Пример:

Задача: вычислить y=|x|.

Дано: х – значение аргумента.

Требуется: у – значение функции. Связь: y =

Словесное представление:

Прочесть значение x.

Записать значение у

Упражнение.Какое значение примет Z в результате выполнения алгоритма

ЕСЛИ X>Y, ТО Z:=X*X+Y

Вид получившейся графической схемы объясняет, почему алгоритм, соответствующий ей, назвали ветвящимся. Кроме того, на схеме наглядно проявляется важное свойство ветвящихся алгоритмов: их исполнение всегда проходит только по одному из возможных путей, который определяется конкретными текущими условиями, причем в каждом случае от начала алгоритма (входа) до его конца (выхода). Это свойство присуще всякому логически правильно составленному алгоритму и является признаком правильной организации ветвлений.

Составляя алгоритм решения задачи о вычислении абсолютной величины заданного значения переменной, мы получили так называемую полную условную конструкцию. Общий вид полной условной конструкции, реализующей ветвление при графическом представлении алгоритма, изображен на рисунке

Здесь Q — проверяемое условие; P₁, P₂, …, P_n — действия, которые должны быть выполнены в случае истинности условия Q (положительная ветвь ветвления); T₁, T₂, …, T_m — действия, выполняемые, если условие Q ложно (отрицательная ветвь ветвления).

При словесном представлении алгоритма полная условная конструкция реализуется командой ветвления вида:

Циклические алгоритмы. Команда повторения

При составлении алгоритмов решения достаточно большого круга задач нередко возникает потребность в неоднократном повторении одних и тех же команд. Алгоритм, составленный с использованием многократных повторений одних и тех же действий (циклов), называется циклическим.

Однако «неоднократно» не значит «до бесконечности». Организация циклов, никогда не приводящая к остановке в выполнении алгоритма (так называемое «зацикливание»), является нарушением требования его результативности — получения результата за конечное число шагов.

Рассмотрим графическое представление циклического блока алгоритма. В него входят в качестве базовых следующие структуры: логический элемент с проверкой условия Р и блок S, называемый телом цикла. Здесь тело цикла S расположено после проверки условия Р (цикл с предусловием), поэтому может случиться, что при определенных условиях блок S не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется цикл-пока. При словесном представлении алгоритма команда, организующая повторение в цикле-пока имеет вид:

Пока Р повторять

S

Конец цикла

Таким образом, если Р не выполняется, то предусмотрен выход из цикла на команду, записанную после строки «Конец цикла». Здесь условие Р — это условие на продолжение цикла.

Возможен другой случай, когда тело цикла S выполняется по крайней мере один раз и будет повторяться до тех пор, пока не выполнится условие Р. Такая организация цикла, когда тело цикла, расположено перед проверкой условия Р, носит название цикла с постусловием или цикла-до. Истинность условия Р в этом случае — причина окончания цикла. Команда, организующая цикл-до, приведена ниже:

Повторять

S

Пока не Р

Конец цикла

Отметим основное отличительное свойство циклических алгоритмов: количество действий, исполняемых в процессе выполнения алгоритма, может существенно превышать количество команд, из которых организован цикл. Чтобы в этом убедиться, достаточно алгоритм «проиграть», то есть выполнить его шаг за шагом при некоторых наборах допустимых исходных данных, перевоплотившись в предполагаемого педантичного исполнителя. (Отметим также, что перед началом этапа программирования полезно проводить указанным образом «проигрывание» любого алгоритма, так как эта процедура позволяет легко обнаружить ошибки, допущенные в логической организации алгоритма).

Для примера напишем блок-схему алгоритма вычисления суммы всех натуральных чисел от 1 до введенного пользователем N. Надо отметить, что можно было бы обойтись линейным алгоритмом, используя формулу суммы n членов арифметической прогрессии. Однако нам интересно именно на этом простом примере проиллюстрировать работу циклического алгоритма.

Наша цель – получить тело цикла, т.е. блок команд, который будет повторяться несколько раз.

Шаг
S:=0;	Усовершенствуем, программу, введя новую переменную i, которая пробегала бы все числа от 1 до 100.	S:=0;		S:=0; i:=0;
S:=S+1;	i:=1; S:=S+i;	i:=i+1; S:=S+i;
S:=S+2;	i:=2; S:=S+i;	i:=i+1; S:=S+i;
S:=S+3;	i:=3; S:=S+i;	i:=i+1; S:=S+i;
…	…	…
S:=S+100;	i:=100; S:=S+i;	i:=i+1; S:=S+i;

Итак, тело нашего цикла:

Найдем условие продолжения цикла. Так как перед входом в цикл значение переменной i равно 0. Поставим условие продолжения , , =. Любой порядковый тип является упорядоченным, но не наоборот. Так вещественные типы и тип string упорядоченные, но не порядковые.

Целые типы

В языке Турбо Паскаль определено 5 целых типов:

Shortint (-128 . 127, 1 байт),

Integer (-32767 . 32768, 2 байта),

Longint (-2147483648 . 2147483647, 4 байта),

Byte (0 . 255, 1 байт),

Word (0 . 65535, 2 байта).

Для целых чисел определены такие операции. Унарные: +,-. Бинарные: сложение, вычитание, умножение, получение частного (div) и остатка (mod) при целочисленном делении и некоторые другие. Также с целыми числами можно производить операции, результаты которых не целые числа. Это обычное деление и операции отношения. Кроме того, имеется большое количество встроенных функций для работы с целыми числами: abs, sqr, sqrt, sin, cos, exp, ln и др.

Вещественные типы

В Турбо Паскале имеется 5 вещественных типов.

Real (занимает 6 байт, диапазон от 2.9E-39 до 1.7E+38 по модулю, точность 11-12 значащих цифр)

Single(занимает 4 байта, диапазон от 1.5E-45 до 3.4E+38 по модулю, точность 7-8 значащих цифр)

Double(занимает 8 байт, диапазон от 5.0Е-324 до 1.7Е+308по модулю,точность 15-16 значащих цифр)

Extended (занимает 10 байт, диапазон от 3.4E-4932 до 1.1E+4932 по модулю, точность19-20 значащих цифр).

Comp(занимает 8 байт, диапазон от -9.2E-18 до 9.2E+18, хранятся точно, поскольку это целые числа)

Вещественные типы являются упорядоченными, но не порядковыми. Операции над вещественными числами: сложение ,вычитание, умножение, деление и операции отношения. Кроме того, имеется большое количество встроенных функций для работы с числами: abs, sqr, sqrt, sin, cos и т.п.

Вещественные числа хранятся неточно. Каждый из имеющихся вещественных типов гарантирует правильное хранение только определенного количества значащих цифр, их называют верными цифрами. С математической точки зрения, из за особенностей внутреннего представления речь идет об относительной погрешности.

Неточности в хранении вещественных чисел могут привести к тому, что при вычитании близких чисел может произойти потеря значимости. Это же объясняет, почему следует избегать сравнения вещественных величин на точное равенство.

ПРИМЕР: тип Single — хранится 7-8 знаков после десятичной точки, тип Double — 15-16, тип Extended — 19-20.

program sravnenie;

var x : single; y : double; z : extended;

Begin

writeln(‘z=’,z);

end.

Эта программа выдаст в результате число z=9.93410748106882E-0009. Обычно принято считать, что a=b, если выполняется условие abs(a-b) 5)

3. Заданное натуральное число N является двузначным и кратно K.

(N >= 10) And (N C) And (A + C > B) And (B + C > A) And

((A = B) Or (B = C) Or (A = C))

(A + B > C) And (A + C > B) And (B + C > A) And

9. Прямоугольник с измерениями A, B подобен прямоугольнику с соответствующими измерениями C, D.

Abs(A / C — B / D) 0)

11. Дано натуральное число N — некоторый год. Этот год является високосным.

(N Mod 4 = 0) And (N Mod 100 0) Or (N Mod 400 = 0)

(N Mod 4 = 0) And Not((N Mod 100 = 0) Xor (N Mod 400 = 0))

Переменные логического типа Boolean занимают в памяти один байт и могут принимать одно из двух значений False — ложное или True — истинное. Этот тип является порядковым (Ord(False) = 0, Ord(True) = 1) и, следовательно, упорядоченным. Результат любых операций сравнения имеет логический тип и может быть присвоен логической переменной. Для операндов типа boolean определены следующие логические операции: NOT — отрицание (превращает false в true, а true в false), AND — логическое умножение «и», OR – логическое сложение «или», XOR — исключающее или (true если операнды разные). Принцип действия этих операций можно проиллюстрировать такими схемами:

Символьный тип

Символьный тип Char также называют литерным. Он позволяет работать с символами, которые записываются двумя способами: в одинарных кавычках или по их коду, например ‘a’, ‘B’, ‘*’ или, что то же самое, #97, #130, #42. В отличие от текста программы на паскале, символы, соответствующие строчным и заглавным буквам различаются. Множество значений типа Char представляет собой полный набор ASCII — символов (американская стандартная кодировка). В компьютере хранятся шестнадцатеричные коды символов (1 байт), которые и используются в операциях отношения (сравнения). Функция Ord выдает код соответствующего символа, который может быть от 0 до 255. Обратной функцией, которая по коду выдает соответствующий символ, является функция Chr.

Дата добавления: 2015-12-08 ; просмотров: 2134 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Решение задач. День первый. Задачи Begin1-10

Итак, с сегодняшнего дня мы начинаем вести новую рубрику: «Решение задач», в которой будем рассматривать задачи, взятые из сборника М.Э.Абрамяна «1000 ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ».

Открыв задачник и прочитав аннотацию, Вы, скорее всего, озадачитесь тем, что данное пособие предназначено для студентов механико-математического, физического и экономического факультетов, но смею Вас заверить, что это весьма универсальная книга, которая подходит как студентам, так и школьникам. Возможно, задачи из первых разделов книги покажутся Вам простыми — в этом случае используйте наш разбор только для проверки своих решений; но если же по каким-либо причинам решить задачи Вы не в состоянии, то тогда присоединяйтесь к нам.

Begin1. Дана сторона квадрата a. Найти его периметр P = 4·a.

Прежде всего напомню, что для ввода и вывода информации, в Паскале используют следующие операторы:

• Read (Readln) — ввод значений с клавиатуры;
• Write (Writeln) — вывод результата (и вообще чего-либо) на экран.

Блок-схема

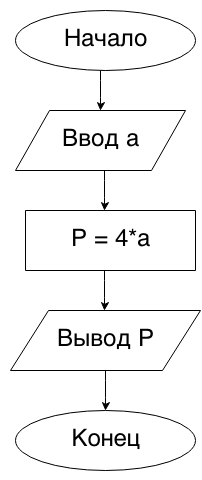
Таким образом, решение задачи становится очевидным.

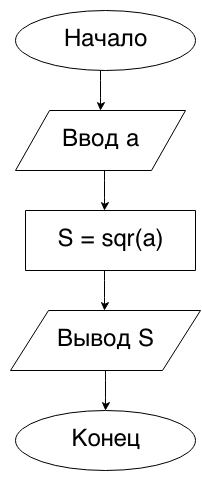
Begin2. Дана сторона квадрата a. Найти его площадь S = a 2 .
При решении данной задачи воспользуемся функцией sqr . Можно, конечно, вычислять квадрат, умножая число само на себя (S=a*a), но при вводе действительно больших чисел наша программа будет выполняться гораздо дольше, нежели при использовании sqr .

Блок-схема

Begin3°. Даны стороны прямоугольника a и b. Найти его площадь S = a·b и периметр P = 2·(a + b).

Да, задача по сути своей проста и подобна предыдущим, поэтому поскорее составим к ней решение и перейдем к следующей.

Блок-схема

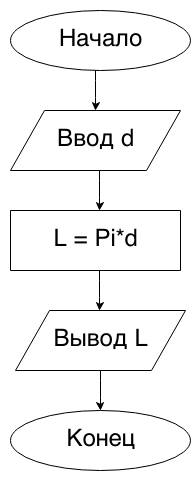
Begin4. Дан диаметр окружности d. Найти ее длину L = π·d. В качестве значения π использовать 3.14.

У вас, наверняка, возникает вопрос π — это константа или переменая? Так как π не изменяется в течение программы, π — константа. Вообще в Паскале уже встроена такая константа, но ее значение:

А так как в условии задачи указано, что в качестве значения π нужно использовать 3.14, то следует объявить π в разделе описания констант.

Блок-схема

Begin5. Дана длина ребра куба a. Найти объем куба V = a 3 и площадь его поверхности S = 6·a 2 .

Для решения задачи используем функцию power(x, a), где a — степень, x — число возводимое в степень (разумеется, использовать ее мы будем только для возведения числа в третью степень, квадрат числа по-прежнему находим с помощью sqr(x) ).

Блок-схема

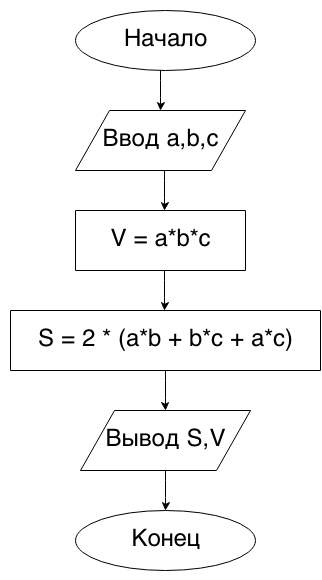
Begin6. Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a·b·c и площадь поверхности S = 2·(a·b + b·c + a·c).

Блок-схема

Begin7°. Найти длину окружности L и площадь круга S заданного радиуса R:
L = 2·π·R, S = π·R 2 .
В качестве значения π использовать 3.14.

Блок-схема

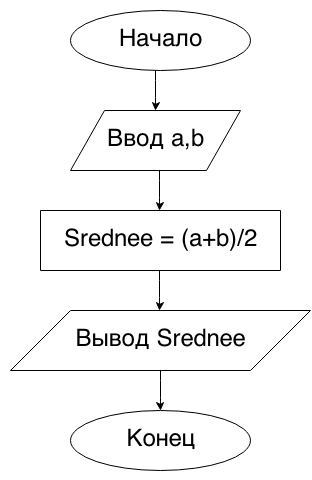
Begin8. Даны два числа a и b. Найти их среднее арифметическое: (a + b)/2.

Блок-схема

Begin9. Даны два неотрицательных числа a и b. Найти их среднее геометрическое, то есть квадратный корень из их произведения: √(a*b).

Напомню, что для нахождения квадратного корня мы используем функцию sqrt .

Блок-схема

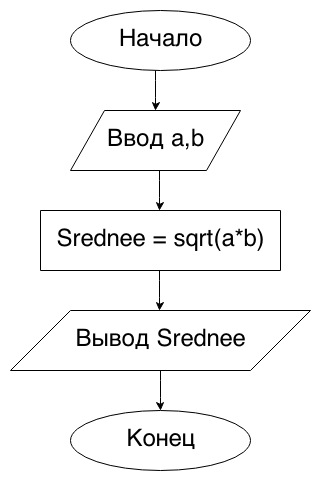
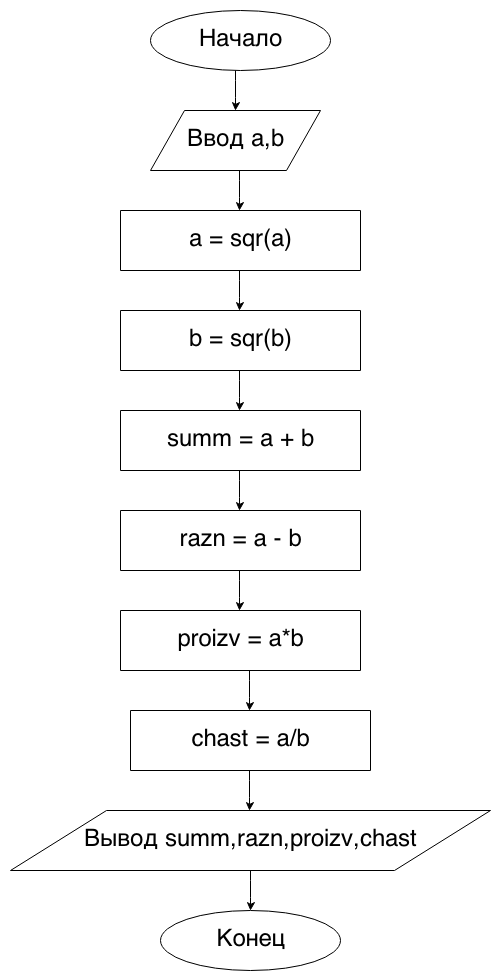
Begin10. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.

Блок-схема

Ну вот и все. Следующая публикация с решением задач выйдет в ближайшие дни.

🎥 Видео