Задание 16. Окружность с центром в точке О пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону АВ в точках K и L так, что АК = 13, KL = 6, LB = 1.
а) ABCD – трапеция, BL – биссектриса, следовательно, 


Аналогично доказывается, что CL перпендикулярна BD. Получаем, что диагонали BD и AC перпендикулярны и в то же время являются биссектрисами углов. Следовательно, трапеция ABCD – это ромб, а у ромба биссектрисы всех углов пересекаются в одной точке.
б) Задача сводится к нахождению высоты ромба. Рассмотрим равнобедренный треугольник OLK, т.к. OL=OK как радиусы одной окружности.
Далее, 
Так как OH – высота прямоугольного треугольника OAB, то
Видео:Геометрия Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хордыСкачать

Окружность высекает на всех сторонах трапеции равные отрезки
Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
a) Расстояние от центра окружности до хорд одинаковой длины равны. Следовательно, точка O равноудалена от прямых AB, BC, CD и AD. Значит, она лежит на биссектрисе каждого из углов трапеции.
б) Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда UW — высота трапеции, а точка V — середина отрезка KL. Значит,
Пусть BH — высота трапеции. В прямоугольном треугольнике ABH имеем:
Приведем решение Максима Волкова.
Опустим из точки O перпендикуляры OU, OV и OW на стороны AD, AB и BC соответственно. Тогда
UW — высота трапеции, а точка V — середина отрезка KL. Тогда
Проведем отрезки АО и ОВ. Заметим, что треугольник AOB прямоугольный, так как АО и ВО — биссектрисы углов трапеции при боковой стороне. Тогда по свойству высоты прямоугольного треугольника находим:
Следовательно, для высоты трапеции получаем:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 520805: 520917 520855 520881 Все
Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Задание 16. ЕГЭ. Окружность с центром в точке О пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
Задание. Окружность с центром в точке О пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону АВ в точках К и L так,
что АК = 19, КL = 12, LВ = 3.
Решение:
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
Если хорды в окружности равны, то они равноудалены от центра окружности.
Это можно доказать, рассмотрев, например, треугольники ΔOKL и ΔОMN:
MN = KL, OL = OM = R, OK = ON = R.
Следовательно, ΔOKL = ΔОMN, а, значит, высоты этих треугольников также будут равны. Аналогично доказывается и с другими хордами.
Т. е. расстояние от центра окружности до всех хорд, а также до сторон трапеции будет одинаково.
Точка О лежит внутри угла ∠BAD и равноудалена от сторон этого угла, значит, по теореме о биссектрисе угла, точка О лежит на биссектрисе АО угла ∠BAD. Получим, ∠1 = ∠2.
Аналогично, ОВ, ОС и ОD – биссектрисы углов трапеции. Получим, что точка О лежит на каждой из четырех биссектрис, значит, и все биссектрисы трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону АВ в точках К и L так, что АК = 19, КL = 12, LВ = 3.
Так как ВС параллельна AD, OE ⊥ BC, OH ⊥ AD, то точки Е, О и Н лежат на одной прямой и ЕН – высота трапеции.
Хорды окружности равны, значит, KF = FL = TE =MH = 6.
Прямоугольные треугольники ΔAFO и ΔAHO равны по гипотенузе и острому углу, тогда AF = AH = 25.
Прямоугольные треугольники ΔBFO и ΔBEO равны по гипотенузе и острому углу, тогда BF = BE = 9.
Рассмотрим прямоугольную трапецию ABEH, в которой АВ = 34, BE = 9, AH = 25.
Опустим перпендикуляр ВР, ВР = ЕН, ВЕ = РН = 9 и АР= АН – РН = 16.
Из прямоугольного треугольника ΔАВР по теореме Пифагора найдем ВР:
🌟 Видео
Задание 16 из реального ЕГЭ по математикеСкачать

Задача про трапецию, описанную около окружностиСкачать

Деклассируем трапецию. Перечневые олимпиады 2021Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Радиус описанной окружности трапецииСкачать

16 ЗАДАНИЕ ОГЭ ИЩЕМ УГОЛ А В ТРАПЕЦИИ ИЗ КРУГАСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Планиметрия. №7. (16 задача ЕГЭ).Скачать

Почему любая вписанная трапеция будет равнобедренной? #геометрияегэСкачать
Радиус вписанной окружности #ShortsСкачать
Задача о площади равнобедренной трапецииСкачать

Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать
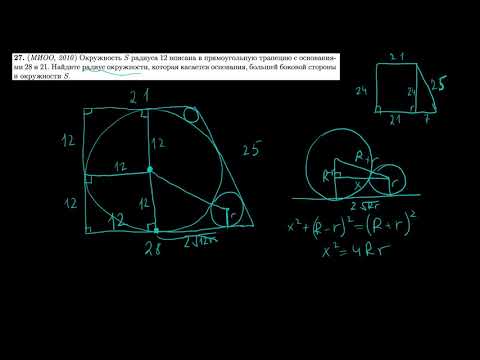
Трапеция и вписанная окружностьСкачать








