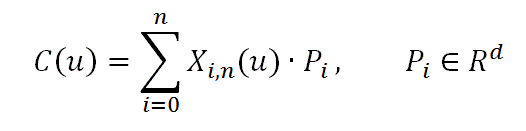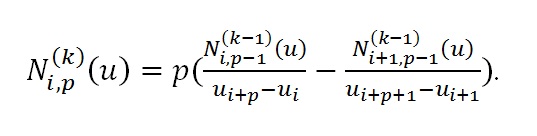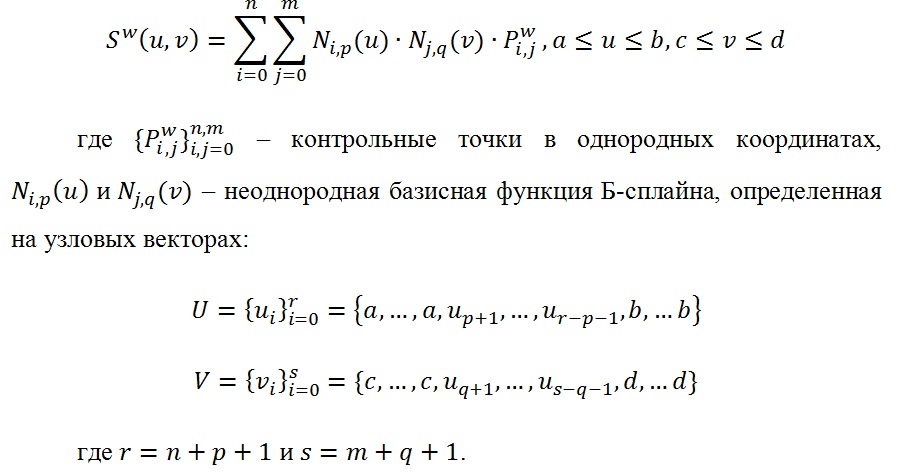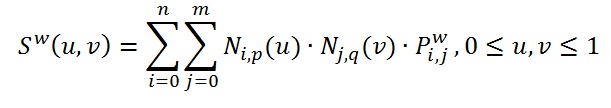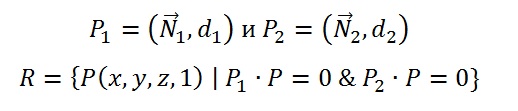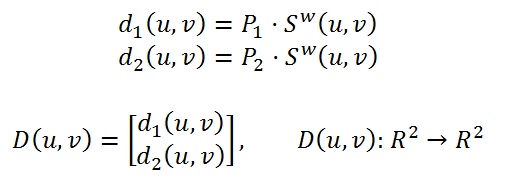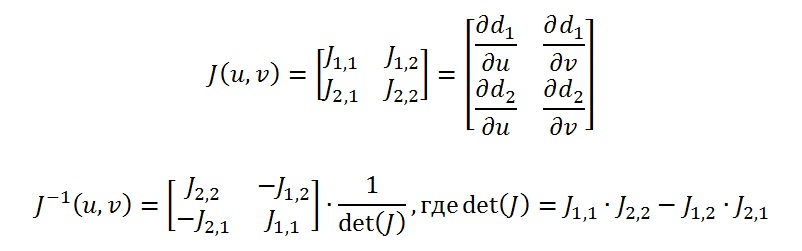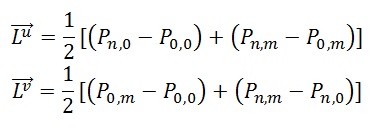B сплайн узловой вектор (7 видео) | Курс школьной геометрии

NURBS

Мозголин Андрей Сергеевич

выпускник Костромского Государственного Университета имени Н.А. Некрасова.

Неоднородный рациональный Б-сплайн, NURBS (от англ. Non-uniform rational B-spline) – математическая модель, применяемая для генерации и представления кривых и поверхностей [13]. NURBS является наиболее простым и универсальным способом задания кривых и поверхностей любой сложности.

Сначала мы рассмотрим математическую модель, описывающую построение NURBS кривых, а затем перейдем к NURBS поверхностям.

Содержание

Полиномиальные параметрические кривые
Неоднородные Б-сплайн кривые
Алгоритмы поиска точек пересечений луча и NURBS поверхности.
B сплайн узловой вектор
5.9. Аппроксимация на основе B-сплайнов
Интерполяция с помощью B-сплайновых кривых Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Котелина Н.О.
Похожие темы научных работ по математике , автор научной работы — Котелина Н.О.
Interpolation with B-spline curves
Текст научной работы на тему «Интерполяция с помощью B-сплайновых кривых»
📺 Видео

Видео:Скоростной перевод растра в вектор при помощи B-сплайнаСкачать

Полиномиальные параметрические кривые

В компьютерной графике широко применяется метод построения кривых по контрольным точкам, т.е. по некоторой ломаной кривой строится гладкая кривая. Данный метод получил широкое распространение благодаря своей простоте и универсальности. Меняя положение контрольных точек, мы можем менять вид кривой. Общий вид формулы, описывающей кривую в параметрической форме [1]:

Функция X[i,n](u) называется базисной функцией и представляет собой полином n – ой степени, P[i] – управляющие коэффициенты, при изменении которых меняется вид кривой. Наиболее широко известными видами базисных функций являются:

— базисная функция Б-сплайна;

Как видно из названия, именно базисная функция Б-сплайна является основой для NURBS кривых и поверхностей, ее мы и будем рассматривать.

Базисная функция Б-сплайна

Пусть U = неубывающая последовательность действительных чисел, т.е. u[i] Рисунок 1. Квадратичные базисные функции определенные на узловом векторе U =

Узловой вектор представляет собой последовательность значений параметров, которые определяют, где начинается и заканчивается базисная функция. Существует два типа узловых векторов: однородные и неоднородные. В однородных узловых векторах значение узлов распределены в векторе с одинаковым шагом, и поэтому в нем нет повторяющихся узлов. В неоднородном векторе значение узлом распределены не равномерно, что позволяет контролировать моменты начала и завершения базисной функции. Неоднородные узловые вектора более универсальны, поэтому говоря об узловых векторах мы будем иметь в виду именно неоднородные.

Узел, который повторяется в узловом векторе раз называют узлом кратности. Свойства базисной функции Б-сплайна:

–N[i,0](u) ступенчатая функция, равна нулю, если u не принадлежит полуинтервалу [u[i], u[i+1]) и единице в противном случае;

— N[i,p](u) >= 0 при любых i,p и u;

— на узловом интервале [u[i], u[i+1] ), «p+1»-ая базисная функция N[i,p](u) не обращается в ноль, а именно функции N[i-p,p](u). N[i,p](u).

— если в функции N[i,p](u), в дроби знаменатель обращается в ноль, то вся дробь обращается в ноль;

— Сумма(от j = i-p до i) = 1 для всех u принадлежащих [u[i], u[i+1] );

— к-ая производная N[i,p](u) будет обозночаться как N[i,p](u) с верхним индексовм (к) в круглых скобках:

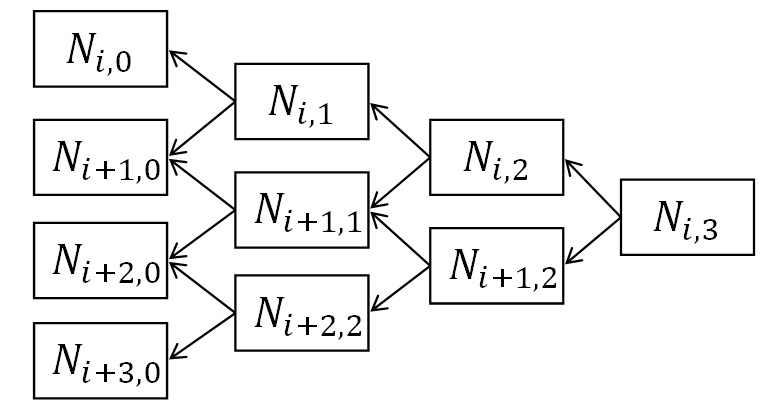
Процесс вычисления базисной функции можно представить в виде следующей схемы:

Видео:РК6. Геометрическое моделирование. B-кривые: B-сплайн функции, часть 2Скачать

Рисунок 2. Процесс вычисления базисной функции.

Видео:РК6. Геометрическое моделирование. B-кривые: B-сплайн функции, часть 1Скачать

Неоднородные Б-сплайн кривые

NURBS поверхности в однородных координатах степени в направлении и степени в направлении задается:

NURBS поверхности имеют следующие важные геометрические свойства, которые в основном аналогичны соответствующим свойствам NURBS кривых:

— граничные значения: S(a,c) = P[0,0], S(b,c) = P[n,0], S(a,d) = P[0,m];

— аффинные преобразования применимы к NURBS поверхностям, т.к. аффинные преобразования применяются к ее контрольным точкам;

— если (u,v) принадлежит [u i , u i+1 ) x [v i , vi+1 ), то S(u,v) определяется выпуклой оболочкой из контрольных точек P i-p,j-q . P i,j ;

— локальная модификация: изменение P i,j или w i,j изменяет поверхность S(u,v) только на прямоугольнике [u i , u i+p+1 ) x [v j , v j+q+1 );

— дифференцируемость: S(u,v) является p-k раз дифференцируемой по u на узле кратности k, и раз q-k дифференцируемой по v на узле кратности k.

Видео:4.1 Интерполяция кубическими сплайнамиСкачать

Алгоритмы поиска точек пересечений луча и NURBS поверхности.

Первый алгоритм появился еще в 1980 году, и с тех пор появилось достаточно много подходов к решению этой проблемы [12] [5]. Но можно выделить лишь несколько основных алгоритмов, поскольку все остальные являются лишь их модификацией. Можно выделить два основных алгоритма, которые не использую тесселяцию:

— итерационный метод Ньютона (Toth, 1985)

— метод отсечения Безье (Nishita, 1990) [9]

Оба метода позволяют численно находить точку пересечения луча и NURBS поверхности. Перед тем как мы перейдем к рассмотрению этих методов необходимо ввести некоторые обозначения.

Пусть у нас есть NURBS поверхность, заданная в виде:

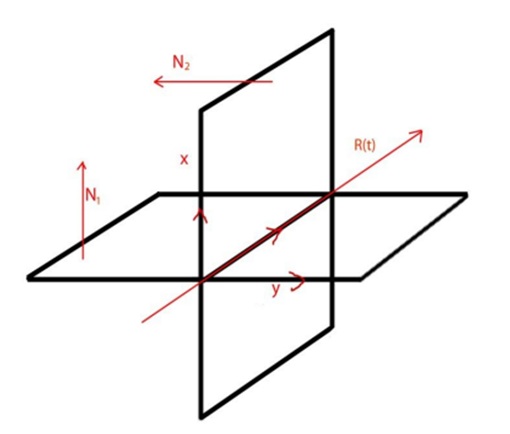
Луч R(t), заданный в параметрическом виде: R(t) = o + d*t, где o – позиция, d – направление. Представим луч также как пересечение двух ортогональных плоскостей и (Рисунок 3).

Где N1 и N2 – нормали плоскостей, d1 и d2 – расстояние от плоскости до начала координат.

Рисунок 3. Луч, как пересечение плоскостей

Определим функции d1(u,v) и d2(u,v), возвращающие расстояние от точки поверхности до плоскостей P1 и P2:

Где матрица Якоби и обратная матрица Якоби вычисляются следующим образом:

где rand(0,1) – случайное вещественное число на полуинтервале [0,1).

Итерационный процесс продолжается до тех пор, пока не выполнится одно из следующих условий:

1. || D(u i ,v i ) || > || D(u i-1 ,v i-1 ) || если новая оценка увеличивает расстояние до луча, то будем считать что, луч не пересекает поверхность;

2. u i ,v i не принадлежат отрезку [0,1], случай рассматривается ниже;

3. i > max , в случае превышения количества итераций считаем, что пересечения нет;

4. || D(u i ,v i ) || (u i ,v i ) решением.

В случае, когда u i ,v i не принадлежат отрезку [0,1], мы могли бы просто считать что, луч не пересекает поверхность, но это приводит к погрешностям на краях поверхности. Это проблема может быть решена следующим образом. Если u i ,v i не принадлежат отрезку [0,1], то мы их зеркально отображаем, чтобы поместить их в область параметров: ( u i = — u i если u i u i = 2- u i если ui > 1). Аналогично с параметром v i . Если || D(u i ,v i ) || (u i ,v i ) решение, в противном случае пересечения нет. Норма D(u i ,v i ) — евклидово расстояник в даумерном пространстве (u,v).

Метод отсечений безье

Пересечение плоскости P k , k= [1,2] и поверхности можно записать как:

В этой проекции плоскость P1 становится осью y, плоскость P2 осью x, а луч проецируется в начало координат.

Сначала мы определим два вектора Lu и Lv и в системе координат:

Вектор Lu должен быть перпендикулярен направлению u, а вектор Lv перпендикулярен направлению v. В этом случае алгоритм отсечения Безье сходится к правильному решению более быстро. Если угловые точки поверхности совпадают, то мы получим нулевые векторы. Этого можно избежать следующим образом:

— если нулевой только один вектор, то его мы берем перпендикулярным не нулевому вектору;

— если оба вектора нулевые, то вычисляем вектора среди других контрольных точек.

Чтобы найти решение уравнения P(u,v) = 0 для направлений Lu и Lv, необходимо выполнить следующий итерационный процесс:

1. Разобьём параметрическую область uv = [a,b] x [c,d] на сетку размером n*m. Шаг по u равен (b-a)/n, по v равен (d-c)/m. Каждому узлу сетки соответствует точка C i,j = P(u i ,v i ), i принадлежит интервалу [0,n], j — интервалу [0,m];

2. Определим двумерное пространство (u,d), состоящего из точек вида: D i,j = (u i ,d i,j ), где d i,j знаковое расстояние от точки C i,j до прямой проходящей через начало координат и направляющим вектором Lu. Аналогично для направления v.

3. В пространстве (u,d) находим отрезок [u min , u max ], на котором d(u) = 0. Аналогично находим [v min , v max ].

Повторяем процесс для области [u min , u max ] x [v min , v max ].

Итерационный процесс завершается в двух случаях:

1. Если на третьем шаге нет значений, на которых d(u)=0 , считаем, что луч не пересекает поверхность.

2. Если размер области меньше некоторого малого значения, считаем, что луч пересекает поверхность в точке с параметрами u = 0.5*(u min + u max ), v = 0.5*(v min + v max ).

NURBS поверхность строиться одинаково, как при использовании итерационного метода Ньютона, так и при использовании метода отсечения Безье.

Итерационный метод Ньютона хоть и является наиболее простым и понятным, но у него есть один существенный недостаток, который выявился в результате тестирования программы. Он существенно зависит от начального приближения. Т.е. если в качестве первого приближения взять, какие то конкретные , то метод может долго сходится к решению или вовсе его не найти. Поэтому, что бы найти наилучшее приближение мы разбиваем нашу плоскость по параметрам на сетку с определенным шагом. В каждом узле сетки считаем точку, которая соответствует этим параметрам. В результате, в качестве первого приближения мы берем ту пару , которой соответствует точка, находящаяся ближе всего к лучу. Данный метод позволяет найти достаточно хорошее приближение и поэтому итоговое решение находится примерно за 5 шагов итерационного метода.

Метод отсечения Безье не требует каких-либо начальных значений, а значит, он более подходит для решения данной проблемы. Единственная сложность, которая возникла в процессе реализации, это определение максимального и минимального значения параметров, на третьем шаге итерационного процесса. Необходимо следить за тем, чтобы интервал не оказался равным нулю или наоборот занимал всю область значений. В этих случаях итерационный процесс может выдать ложное решение или не сходится к решению.

Рисунок 4. Результат работы трассировщика лучей с NURBS поверхностью.

Для решения этой задачи наиболее подходит метод отсечения Безье. Он не зависит от начальных условий и в большинстве случаев позволяет получить NURBS поверхность без артефактов. Существует несколько проблем, но по сравнению с основной проблемой итерационного метода Ньютона, они менее значительные. Говоря в общем, о применении NURBS поверхностей в трассировке лучей, трассировка NURBS значительно увеличивает время рендеринга сцены по сравнению с трассировкой других видов поверхностей.

Видео:Урок 4. CorelDraw. Инструмент "B-сплайн", "Свободная форма". Создание, редактирование контура фигурСкачать

B сплайн узловой вектор

Видео:РК6. Геометрическое моделирование. B-кривые: алгоритмы построенияСкачать

5.9. Аппроксимация на основе B-сплайнов

Основу метода Безье составляет аппроксимация многочленами Бернштейна. Однако можно выбрать и другие наборы базисных функций, например B-сплайны , по отношению к которым базис Бернштейна является частным случаем. В сравнении с многочленами Бернштейна B-сплайны обладают следующими дополнительными преимуществами [15], [16]:

1. Аппроксимация B-сплайнами обеспечивает более точное приближение ломаной, чем аппроксимация многочленами Бернштейна.

2. При аппроксимации методом Безье на значения координат каждой точки кривой оказывают влияние все вершины ломаной Безье. Это затрудняет корректирование отдельных участков кривой. В то же время аппроксимация B-сплайнами обладает желательной локальностью. Этим способом можно производить локальные изменения кривой без полного пересчета.

3. Единственным путем увеличения (уменьшения) порядка кривой Безье является увеличение (уменьшение) числа вершин и соответствующей ломаной Безье. В методе B-сплайнов эти два параметра независимы и, следовательно, могут быть выбраны произвольно.

Кривая, построенная на основе B-сплайн -базиса, описывается следующим образом [см. СПИСОК ЛИТЕРАТУРЫ]:

(5.13)

(5.14)

Здесь x_i – элементы узлового вектора , а t – параметр, изменяющийся в диапазоне от 0 до t_max =( n – k +2) .

Рис.5.9. Изображение нескольких B-сплайн -кривых различного порядка.

Узловой вектор, длина которого ( n+k +1) , вводится для учета собственной кривизны B-сплайн -кривых и представляет собой неубывающую последовательность целых чисел — параметрических узлов . Узловой вектор определяется числом точек в аппроксимируемой ломаной, порядком кривой, а также наличием сложных (кратных) узлов.

Из (5.13) и (5.14) следует, что B-сплайн -кривая является полиномом степени ( k –1) на каждом интервале ( x_i, x_{i +1}) и что все ее производные до ( k –2) -го порядка включительно непрерывны вдоль всей кривой. То есть эта кривая представляет собой сплайн-функцию порядка k (степени k –1 ).

На рис.5.9 изображены несколько B -сплайн-кривых различного порядка, аппроксимирующих ломаную с шестью вершинами. При этом кривая пятого порядка является кривой Безье для заданной ломаной, кривая четвертого порядка — кубическим сплайном, а кривая второго порядка — последовательностью связанных отрезков, совпадающих с исходной ломаной. Представляет интерес также кривая третьего порядка — она касается внутренних отрезков ломаной в их средних точках. Заметим, что с ростом порядка B-сплайн -кривые как бы спрямляются, их форма все в большей степени становится отличной от аппроксимируемой ломаной.

Рис.5.10. B-сплайн -кривые со сдвоенной вершиной. В этой вершине в кривой третьего порядка образуется излом

В формируемые кривые можно вносить изломы путем включения в соответствующую ломаную кратных вершин. Так, для образования излома в кривой третьего порядка необходима сдвоенная вершина (рис.5.10). А чтобы создать излом в кривой четвертого порядка, потребуется вершина с кратностью три и т. д.

Большое количество примеров, иллюстрирующих различные способы построения B-сплайн -кривых, читатель может найти в [см. СПИСОК ЛИТЕРАТУРЫ].

Аппроксимация B-сплайнами реализована в программах BSPLN2 и BSPLN3 . Первая из них предназначена для формирования плоских, а вторая — пространственных B-сплайн -кривых.

Программа BSPLN2 (K,XP,YP,NPLG,XC,YC,NPTS,WFUN,NWF,VKNOTS,NKNOTS) позволяет вычислить значения координат точек плоской B-сплайн -кривой, аппроксимирующей заданную совокупность точек. Программа имеет следующие параметры:

K порядок аппроксимирующей кривой (ее степень равна K -1), 2 K NPLG ; XP,YP векторы значений соответственно X -, и Y -координат заданной совокупности точек (аппроксимируемой ломаной) длины NPLG ; NPLG число точек в аппроксимируемой ломаной; XC,YC векторы значений соответственно X -, и Y -координат аппроксимирующей B-сплайн -кривой (длины NPTS ); NPTS число точек в аппроксимирующей B-сплайн -кривой; WFUN двумерный рабочий массив, предназначенный для размещения весовых функций B-сплайн -базиса, размером (NW,K) ; NWF максимальное значение, принимаемое первым индексом рабочего массива WFUN , NWF = ( NPLG+K -1); VKNOTS одномерный рабочий массив, предназначенный для размещения элементов узлового вектора, длины NKNOTS ; NKNOTS длина узлового вектора, NKNOTS = ( NPLG+K ) .

Программа BSPLN3 (K,XP,YP,ZP,NPLG,XC,YC,ZC,NPTS,WFUN,NWF,VKNOTS,NKNOTS) позволяет вычислить значения координат точек пространственной B-сплайн -кривой, аппроксимирующей заданную совокупность точек. Параметры программы следующие:

XP,YP,ZP векторы значений соответственно X -, Y — и Z -координат заданной совокупности точек аппроксимируемой ломаной длины NPLG ; XC,YC,ZC векторы значений соответственно X -, Y — и Z -координат аппроксимирующей B-сплайн -кривой длины NPTS .

Остальные параметры имеют то же значение, что и в программе BSPLN2 .

В программах BSPLN2 и BSPLN3 используются служебные программы KNOTV2 (K,XP,YP,NPLG,VKNOTS,NKNOTS) и KNOTV3 (K,XP,YP,ZP,NPLG,VKNOTS,NKNOTS) с помощью которых строятся узловые векторы соответственно для двумерного и трехмерного случаев. Параметры этих программ имеют то же значение, что и в программах BSPLN2 и BSPLN3 .

Ниже приведена программа, с помощью которой выполнялось построение рис.5.10.

Видео:Сплайн функция. Идеология построенияСкачать

Интерполяция с помощью B-сплайновых кривых Текст научной статьи по специальности « Математика»

Видео:Коллинеарность векторовСкачать

Аннотация научной статьи по математике, автор научной работы — Котелина Н.О.

Статья посвящена задаче интерполяции точек при помощи B-сплайновых кривых. Рассматриваются методы глобальной интерполяции , при которых составляется и решается система линейных уравнений.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Interpolation with B-spline curves

This article deals with the problem of interpolation with polynomial Bspline curves. It examines methods of global interpolation when systems of linear equations are set up and solved.

Видео:Разложить вектор m по векторам a,b,cСкачать

Текст научной работы на тему «Интерполяция с помощью B-сплайновых кривых»

ПРИКЛАДНАЯ МАТЕМАТИКА И МЕХАНИКА

Вестник Сыктывкарского университета. Серия 1: Математика. Механика. Информатика. Выпуск 1 (21). 2016

ИНТЕРПОЛЯЦИЯ С ПОМОЩЬЮ В-СПЛАЙНОВЫХ

Статья посвящена задаче интерполяции точек при помощи B-сплайновых кривых. Рассматриваются методы глобальной интерполяции, при которых составляется и решается система линейных уравнений.

Ключевые слова: NURBS, B-сплайн кривые, интерполяция.

1. Определение NURBS

Пусть заданы натуральные L, m. Рассмотрим узловой вектор T = (t0. , tL+m+1), где ti G R и ti 0, р 0, г € 0 : Ь.

Построим стыковочные функции вида

Rk (t) = LWfcNk’m(t) . (2)

Тогда дробно-рациональная B-сплайновая кривая степени m задается следующим образом [1] — [4]:

P (t) = Y, Pk Rk (t)- (3)

Поскольку узловой вектор T обычно берётся неравномерный, т. е. узлы являются неравноотстоящими, то кривая (3) называется NURBS-кривой, где аббревиатура NURBS означает non-uniform rational basis spline (неравномерный рациональный базисный сплайн).

При этом если все веса будут равны между собой, то по свойствам базисных функций [1, с. 57] получаем кусочно-полиномиальную B-сплайновую кривую степени m:

P (t)= £ JLk У’ = £ Pk Nkm(t). (4)

2. Интерполяция с помощью Б-сплайновых кривых

Пусть есть набор точек г = 0. ,Ь>. Построим кусочно-по-

линомиальную В-сплайновую кривую С порядка р +1 (степени р), которая проходит через эти точки [1]. Для этого найдём полюса ь=0. Сопоставим каждой точке Qi некоторое значение параметра щ £ [0, 1] и подберём соответствующий узловой вектор и = , где т = Ь + р +1. Получим систему из Ь + 1 уравнения:

Qi = С (щ) = Рк Щр(щ), г = 0. Ь. (5)

Следуя [1, с. 364], решим систему относительно точек Рк, к £ 0. , Ь. Для этого выберем значения параметра щ так, как это сделано в [1]. Рассмотрим величину С :

и0 = 0, иь = 1, иг = иг-1 +

Теперь найдем узлы по следующим формулам:

ио = ■ ■ ■ = ир = з+р-1

Этот метод выбора узлов отражает распределение значений параметра «г ( [1, с. 365]).

ПРИМЕР 1. Рассмотрим точки (Зг>2=0 на плоскости (в [3, с.219] используется 18 узлов и параметрический кубический сплайн). Тогда, используя формулы (6), (7), (8) и решая систему (5) относительно полюсов (Рг>2=0, получаем при р = 6 В-сплайновую кривую (рис. 1).

Рис. 1. Интерполяция с помощью В-сплайновой кривой

3. Интерполяция при помощи Б-сплайновой кривой с заданием производных

Рассмотрим теперь интерполяцию, при которой задаются не только исходные точки г = 0. , Ь, но и производные в этих точках г = 0, . . . , Ь, определяющие направление касательного вектора к искомой кривой [1]. Таким образом, имеем 2(Ь + 1) пар чисел и систему

относительно 2(Ь + 1) полюсов Рк, к = 0. , 2Ь + 1:

Qi = С(мц) = ^ Рк к=0 2Ь+1

Количество узлов в узловом векторе и равно 2(Ь +1) + р +1. Сами узлы можно вычислять по формулам, аналогичным (8), например при р = 3 имеем:

м1 2м1 + и2 и1 + 2и2

23 Мь-2 + 2мь-1 Ть-1 + 1

Решая систему (9) при р = 3 для точек из Примера 1 при разных значениях полученных умножением на коэффициент к соответствующих векторов, вычисленных для уравнения В-сплайновой кривой С из пункта 2, а в крайних точках заданных приближенно, получаем В-сплайновые кривые, показанные на рис. 2.

Рис. 2. Интерполяция В-сплайновой кривой с производными: (а) к = 0.8, (Ь) к = 1.2, (с) к = 1

4. Методы локальной интерполяции

Также существуют методы локальной интерполяции [1, с. 382]. В этом случае по исходному набору точек <Qi, i = 0, строим

сегменты кривых |=0 таким образом, чтобы точки Qi и Qi+1 были конечными точками сегмента Ci. При этом требуем, например, чтобы выполнялось свойство непрерывности первой производной.

1. Piegl L., Tiller W. The NURBS book. 2nd Edition. New York: Springer-Verlag, 1995 — 1997. 327 р.

2. Голованов Н. Н. Геометрическое моделирование. М.: Изд-во Физико-математической литературы, 2002. 472 с.

3. Завьялов Ю. С. , Квасов Б. И. , Мирошниченко В. Л. Методы сплайн-функций. М.: Наука, 1980. 350 с.

4. Хилл Ф. OpenGL. Программирование компьютерной графики. Для профессионалов. СПб.: Питер, 2002. 1088 с.

СГУ им. Питирима Сорокина Поступила 20.09.2016

Kotelina N. O Interpolation with B-spline curves

This article deals with the problem of interpolation with polynomial B-spline curves. It examines methods of global interpolation when systems of linear equations are set up and solved. Keywords: NURBS, B-spline curves, interpolation.

1. Piegl L., Tiller W. The NURBS book. 2nd Edition. New York: Springer-Verlag, 1995-1997. 327 p.

2. Golovanov N. N. Geometricheskoe modelirovanie (Geometric modeling). Moscow: Izd. Fiz.-Mat. Lit., 2002. 472 p.

3. Zavyalov Y. S. , Kvasov B. I. , Miroshnichenko V. L. Metody splayn-funkcij (Methods of spline functions). Moscow: Nauka, 1980. 350 p.

4. Hill F. OpenGL. Programmirovanie komputernoy grafiki (Computer Graphics Programming). Dlya professionalov. SPb.: Piter, 2002. 1088 p.

Для цитирования: Котелина Н. О. Интерполяция с помощью B-сплайновых кривых // Вестник Сыктывкарского университета. Сер. 1: Математика. Механика. Информатика. 2016. Вып. 1 (21). C. 3-8.

For citation: Kotelina N. O. Interpolation with B-spline curves // Bulletin of Syktyvkar University. Series 1: Mathematics. Mechanics. Informatics. 2016. №1 (21). Pp. 3-8.