Аксонометрия куба с вписанными в него окружностями

Окружность в прямоугольной изометрии

Окружности, вписанные в грани куба ( рис 9.6а ), проецируются в эллипсы, В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу, но расположены различно (рис 9.6.б) . Их малые оси всегда располагаются по направлению отсутствующей в данной плоскости аксонометрической оси, а большая ось к ней перпендикулярна.

Существует несколько способов построения окружности в

Первый способ. Строят ромб со стороной, равной D окружности. Точки А и В — центры больших дуг радиуса R, Точки С и Е — центры малых дуг радиуса г. Точки 1, 2, 3. 4 — точки сопряжения дуг (рис 9.7а ).

Второй способ. Проводят две окружности, одна — диаметром, равным большой оси овала (АВ = 1,22 D), вторая — диаметром, равным малой оси (СЕ = 0,71 D). Точки Oi и Oi — центры больших дуг овала, а точки Оз и 04 — центры малых дуг. Точки 1, 2, 3, 4 — точки сопряжения дуг (|рис 9.7i, б).

На рис 9-8 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяем точки 1 и 2. Отрезок 1 — 2 — малая ось эллипса. Из точек 1 и 2, как из центров, описываем дуги радиусом 1 — 2 до их взаимного пересечения. Отрезок 3 — 4 — большая ось эллипса.

9.4.2. Окружность в прямоугольной диметрии

В прямоугольной диметрической проекции так же, как в прямоугольной изометрии, малые оси всех трех эллипсов расположены по направлению той аксонометрической оси, которая отсутствует в плоскости, содержащей эллипс.

На рис.9.9 показаны эллипсы, принадлежащие отдельнмм координатным плоскостям, и указаны размеры их осей. У эллипса, расположенного в плоскости x’0’z’, большая ось равна 1,06 D., малая — 0,94 D.

Эллипсы, принадлежащие координатным плоскостям x ¢ О ¢ y ¢ и z’Oy’ по величине и форме одинаковы. Большие оси этих эллипсов равны 1,06 D, малые — 0,35 D.

На риc.9.9 дано построение диметрического овала для окружности диаметра D, расположенной в плоскости x’O ¢ z ¢

Проводят оси диметрической проекции x ¢ y ¢ z ¢ , затем через точку О проводят прямую, перпендикулярную к оси у’, и на ней откладывают большую ось эллипса АВ. Малую ось эллипса CD откладывают на оси у! Отрезки ОМ = ON = OK = ОЕ равны радиусу данной окружности. Точки М, N, К и Е будут точками сопряжения дуг овала. Точки Oi, Oi, Оз и 04 будут центрами дуг радиусов окружностей, из которых состоит овал.

На рис.9.10 приведено построение диметрических овалов, заменяющих эллипсы, для окружностей, расположенных в плоскостях Н и W, Эти овалы одинаковы по форме и величине. Малая ось имеет направление той аксонометрической оси, которая отсутствует в плоскости, содержащей эллипс, большая ось к ней перпендикулярна.

Последовательность построения такая (рис 9.11, а): от центра О’ на продолжении малой оси эллипса откладываем размер 1,06 D (величину большой оси). Получаем точку O1- центр нижней дуги радиуса R, Из точки О2 этим же радиусом проводим верхнюю дугу овала. От точек А и В откладываем размеры малой оси, уменьшенной в четыре раза, т.е. EF / 4. Из полученных центров Оз, О4 проводим дуги радиуса R1= O’E/2. Точки сопряжения 5 и 6 находим, соединяя прямой точки O1 и О4(О2 и О4) и

продолжая эту прямую до пересечения с дугой.

Построение овала в плоскости W (рис 9.11 б) аналогично построению овала в плоскости Н.

9.4.3. Окружность в косоугольной фронтальной диметрии

На рис.9.12 изображен куб, выполненный в косоугольной фронтальной диметрии. В каждую грань куба вписана окружность. Одна из них, расположенная в плоскости V, проецируется без искажения; две другие — в виде эллипсов, где большая ось равна 1,07D, a малая — 0,33 D. Большие оси эллипсов перпендикулярны недостающим аксонометрическим осям плоскости, в которой они расположены.

Способ построения этих овалов такой же, как в прямоугольной диметрии.

9.5. Примеры построения стандартных аксонометрий

Аксонометрическую проекцию точки А строят по ее координатам ха, уa, za. На рис 9.13, а даны две проекции осей координат и точки. Чтобы построить изометрию точки, от точки О’ на оси х’ откладывают координату ха ( рис 9.13 б). Через полученную точку проводят прямую, параллельную оси у’ и откладывают на ней координату уА Отмечают вторичную проекцию А ¢ 1 точки А, затем откладывают координату za, параллельно оси z ¢ . Полученная точка А — изометрическая проекция точки. Итак, любую аксонометрическую проекцию точки можно получить, построив в аксонометрии трехзвенную координатную ломаную линию, определяющую положение этой точки относительно начала координат.

Аксонометрические проекции прямых, кривых строят по координатам их точек. На рис 9.14 показано построение отрезка АВ, на рис 9.15 показано построение плоской кривой, а на рис 9.16 — пространственной кривой в изометрической проекции

Построение шестигранной призмы по данному чертежу начинают с плоской фигуры основания (рис 9.171). Основание призмы строят по координатам его точек. На изометрической оси г’ откладывают высоту Н, проводят линии, параллельные осям х ‘и у.’ Отмечают на линии, параллельной оси х,’ положение точек 1 и 4.

Для построения точки 2 определяют координаты этой точки на чертеже — х2; и у2; и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.

Построенные точки верхнего основания соединяют между собой. Боковые ребра призмы являются горизонтально — проецирующими

прямыми, поэтому на горизонтальную плоскость проекции Н они проецируются в виде точек. Из точки 1 проводят ребро до пересечения с осью х! затем — ребра из точек 2, 3, 6. Нижнее основание призмы проводят параллельно верхнему. Невидимые ребра призмы следует проводить штриховой линией.

Построение аксонометрической проекции прямого кругового конуса начинают с его основания (рис 9.18).

Аксонометрической проекцией основания будет эллипс, расположенный в плоскости Н. Далее из центра эллипса откладывают высоту конуса. Полученную точку — вершину конуса — соединяют двумя касательными с основанием. На | рис9.18а дано изображение конуса в прямоугольной изометрии, на рис.9.18 б — в прямоугольной диметр ии.

Прямоугольной аксонометрической проекцией сферы диаметром D является окружность, диаметр которой равен 1,22 D (изометрия) или 1,06 D (диметрия) по приведенным коэффициентам искажения. На рис.9.19 а изображена прямоугольная изометрия сферы с вырезом одной восьмой его части. На рис.9-19, б — прямоугольная диметрия сферы с вырезом одной восьмой его части. Три эллипса на изображении — проекции сечения шара координатными плоскостями.

На рис.9.20 изображена прямоугольная диметрия части тора. Сначала строят ось поверхности в виде овала, затем радиусом образующей сферы проводят окружности, равномерно располагая их по направляющей.

Для изображения кольца проводят плавную касательную ко всем окружностям. Чтобы спроецировать любую поверхность вращения (рис.9.21) вписывается в неё произвольные сферы, при этом 0 ¢ 1 ¢ =0 ² 1 ² и т.д. Плавная касательная ко всем окружностям представляет собой контур изображения .При построении ксонометрии по приведенным показателям искажения радиусы вписываемых сфер увеличиваются в изометрии в 1,22 раза, в диметрии — в 1,06

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Изображение окружностей в изометрической проекции

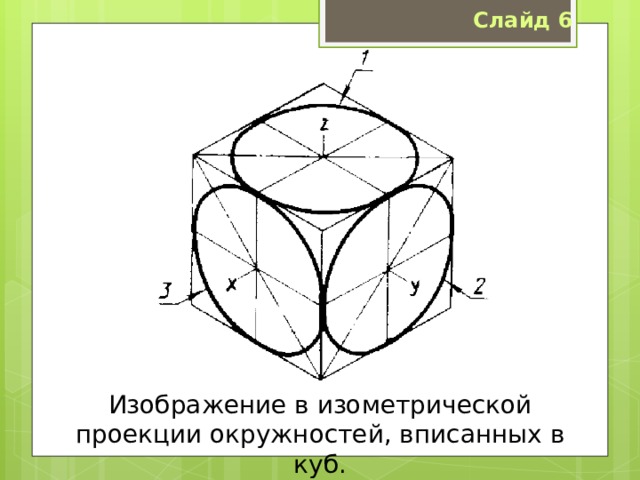
Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16. Изометрические проекции окружностей, вписанных в грани куба

Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17. Построение овала

Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db).

Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

Построение изометрических проекций деталей

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б) и окружности (рис. 3.18, в).

Рис. 3.18. Последовательность построения изометрической проекции детали

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г).

Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Видео:Окружности в изометрических проекциях.Скачать

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Видео:Прямоугольная изометрическая проекция кубаСкачать

Аксонометрия окружности в кубе

Видео:2 2 3 построение изометрии окружностиСкачать

Изображение окружностей в изометрической проекции

Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16. Изометрические проекции окружностей, вписанных в грани куба

Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17. Построение овала

Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db).

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Построение изометрических проекций деталей

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б) и окружности (рис. 3.18, в).

Рис. 3.18. Последовательность построения изометрической проекции детали

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г).

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Видео:Аксонометрические проекцииСкачать

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Видео:Построение аксонометрии моделиСкачать

Аксонометрические проекции окружности

Просмотр содержимого документа
«Аксонометрические проекции окружности»

Аксонометрические проекции окружностей

Окружность в аксонометрии

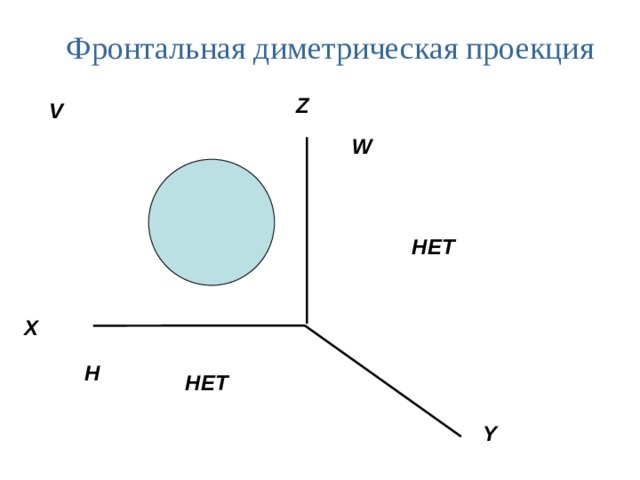
Фронтальная диметрическая проекция

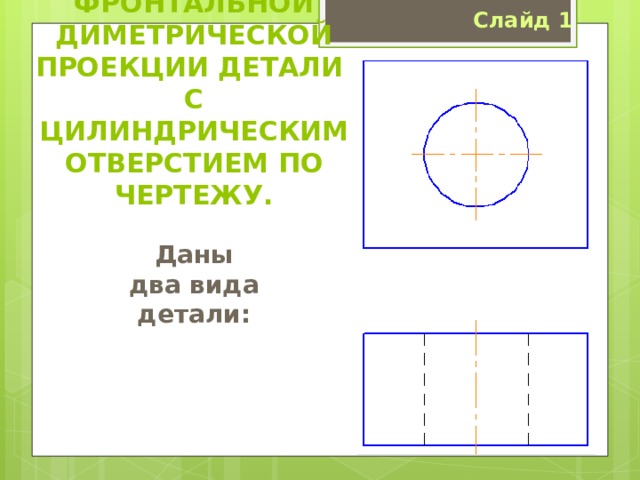
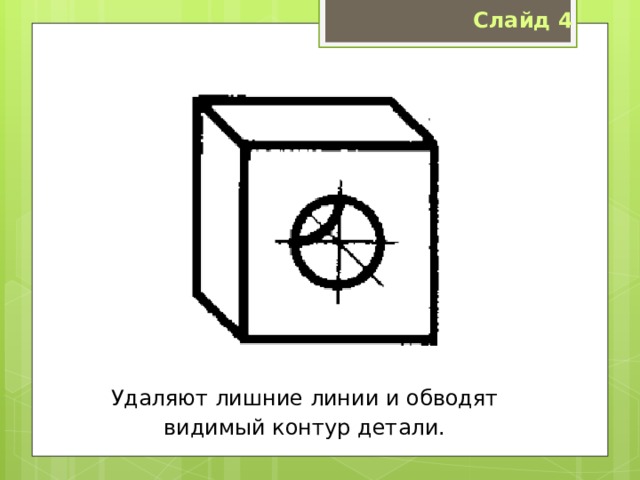
Построение фронтальной диметрической проекции детали

с цилиндрическим отверстием по чертежу.

Даны два вида детали:

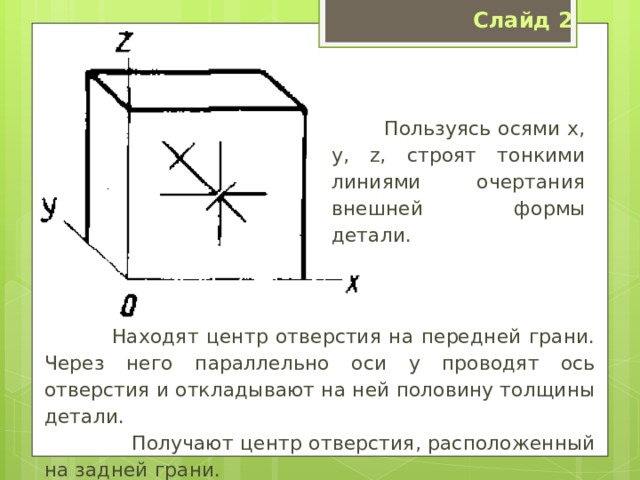
Пользуясь осями x, y, z, строят тонкими линиями очертания внешней формы детали.

Находят центр отверстия на передней грани. Через него параллельно оси y проводят ось отверстия и откладывают на ней половину толщины детали.

Получают центр отверстия, расположенный на задней грани.

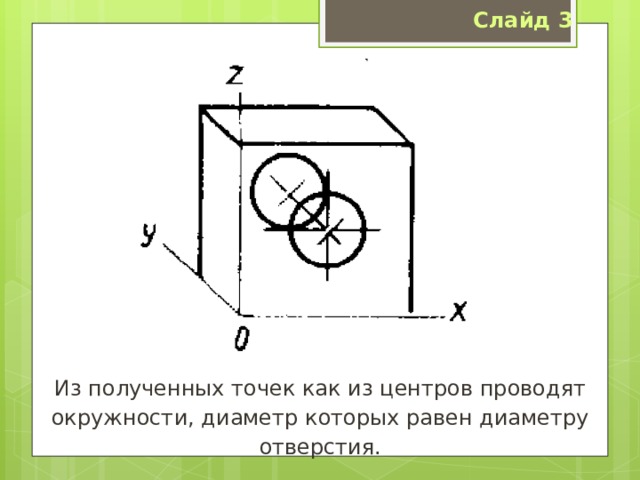
Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия.

Удаляют лишние линии и обводят видимый контур детали.

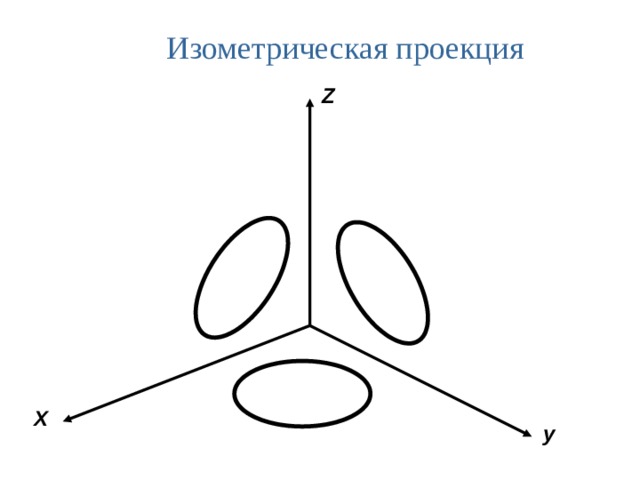
Изометрические проекции окружностей

Изометрической проекцией окружности является эллипс. В практике черчения вместо него строят овал.

Овал – замкнутая кривая, очерченная дугами окружностей.

Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.

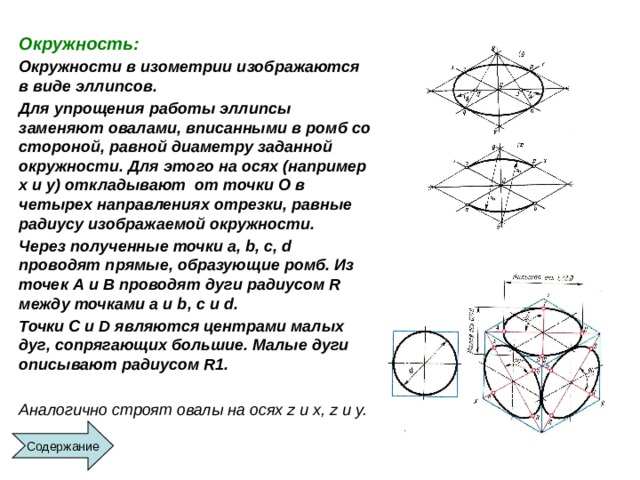
Окружности в изометрии изображаются в виде эллипсов.

Для упрощения работы эллипсы заменяют овалами, вписанными в ромб со стороной, равной диаметру заданной окружности. Для этого на осях (например x и y) откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности.

Через полученные точки a, b, c, d проводят прямые, образующие ромб. Из точек А и В проводят дуги радиусом R между точками a и b, c и d.

Точки C и D являются центрами малых дуг, сопрягающих большие. Малые дуги описывают радиусом R1.

Аналогично строят овалы на осях z и x, z и y.

Изображение в изометрической проекции окружностей, вписанных в куб.

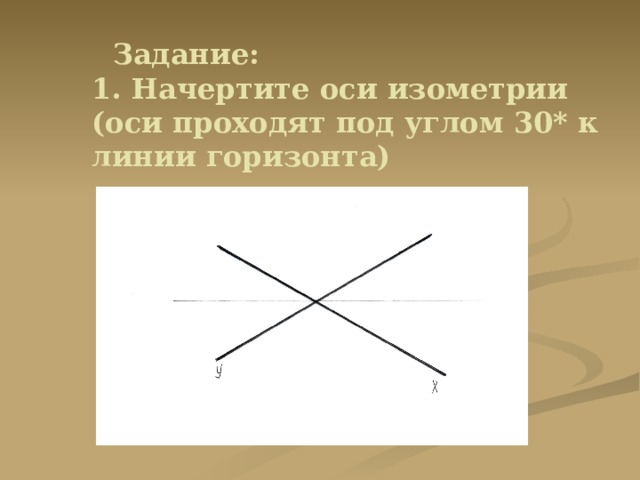
Задание: 1. Начертите оси изометрии (оси проходят под углом 30* к линии горизонта)

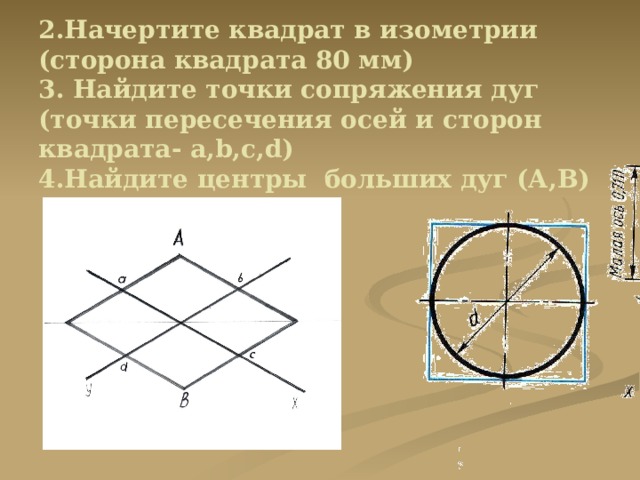
2.Начертите квадрат в изометрии (сторона квадрата 80 мм) 3. Найдите точки сопряжения дуг (точки пересечения осей и сторон квадрата- а,b,c,d) 4.Найдите центры больших дуг (А,В)

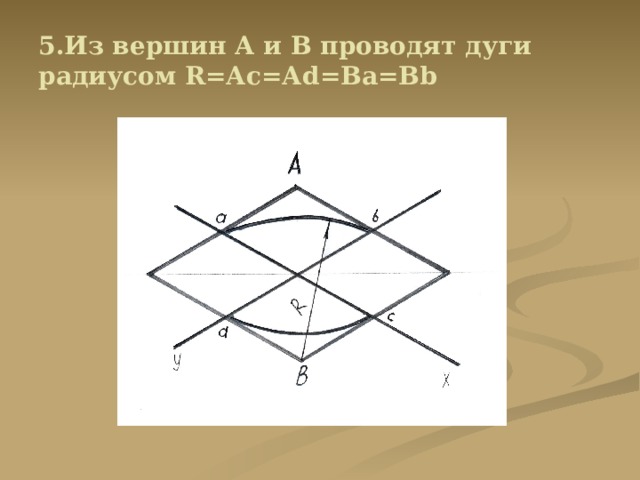
5.Из вершин А и В проводят дуги радиусом R=Ас=Аd=Ва=Вb

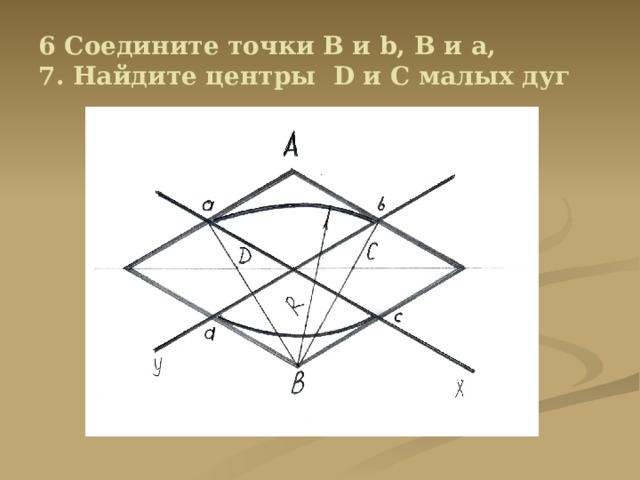
6 Соедините точки B и b, В и а, 7. Найдите центры D и С малых дуг

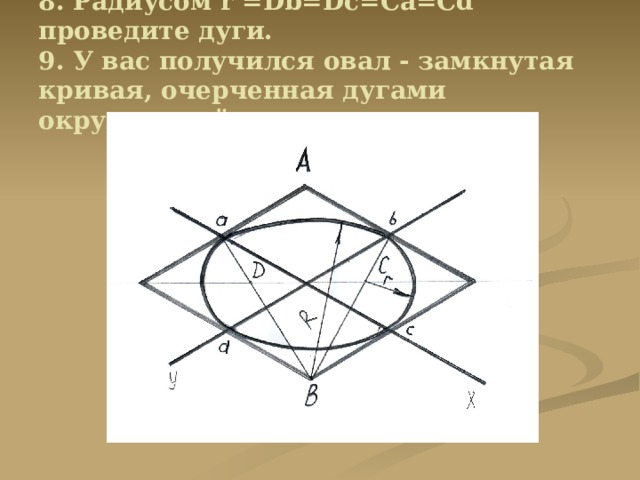
8. Радиусом r =Db=Dc=Ca=Cd проведите дуги. 9. У вас получился овал — замкнутая кривая, очерченная дугами окружностей.

10.Начертите куб в изометрической проекции и впишите в каждый ромб овал

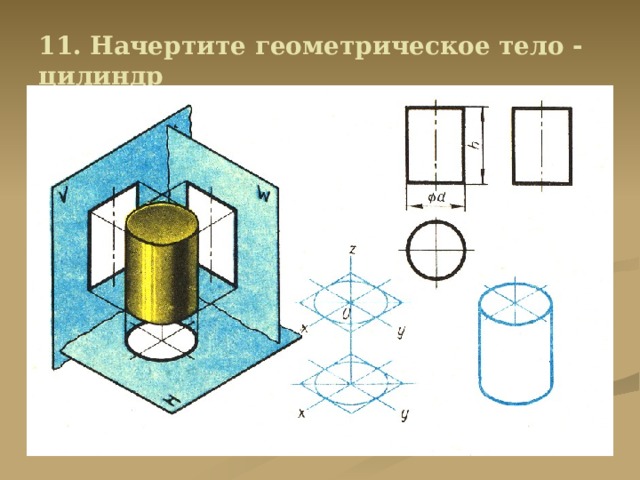
11. Начертите геометрическое тело — цилиндр

• Как называется окружность выполненная в осях изометрии?
• Как называется геометрическая фигура при вычерчивании квадрата в осях изометрии?
• Сколько центров надо найти при вычерчивании овала?
• Чем на чертеже являются точки a, b, с, d?

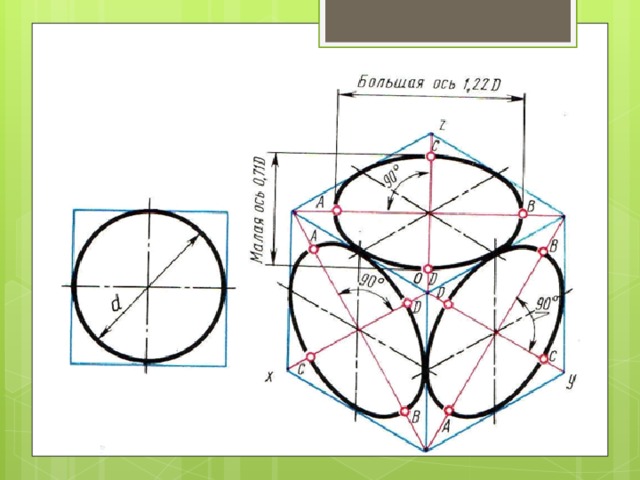
Построение овала, вписанного в ромб

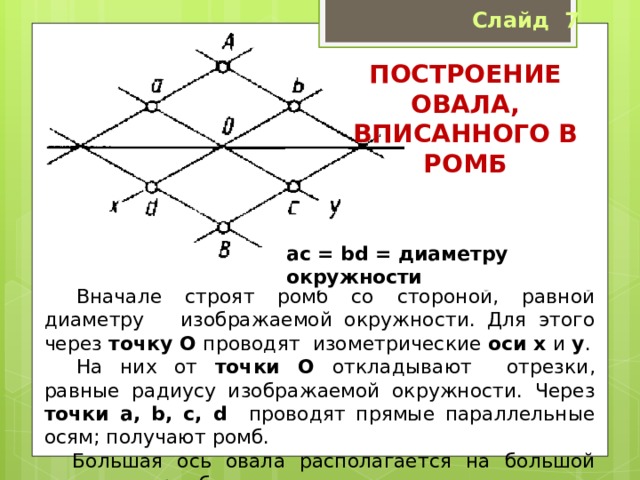
ас = bd = диаметру окружности

Вначале строят ромб со стороной, равной диаметру изображаемой окружности. Для этого через точку О проводят изометрические оси x и y .

На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с, d проводят прямые параллельные осям; получают ромб.

Большая ось овала располагается на большой диагонали ромба.

Построение овала, вписанного в ромб

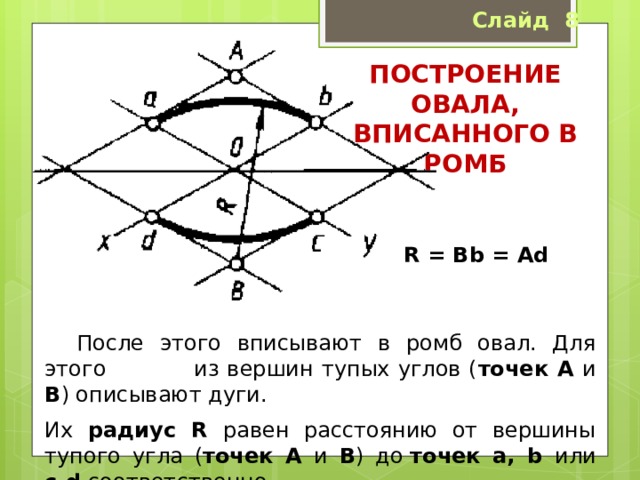
После этого вписывают в ромб овал. Для этого из вершин тупых углов ( точек А и В ) описывают дуги.

Их радиус R равен расстоянию от вершины тупого угла ( точек А и В ) до точек а, b или с,d соответственно.

Построение овала, вписанного в ромб

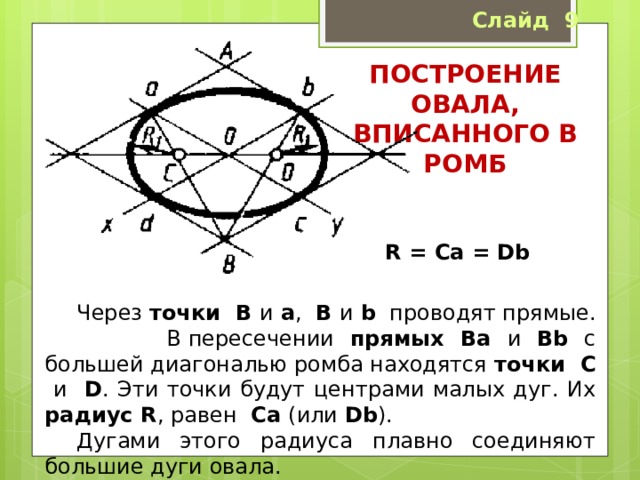
Через точки B и a , B и b проводят прямые. В пересечении прямых Ba и Вb с большей диагональю ромба находятся точки C и D . Эти точки будут центрами малых дуг. Их радиус R , равен Сa (или Db ).

Дугами этого радиуса плавно соединяют большие дуги овала.

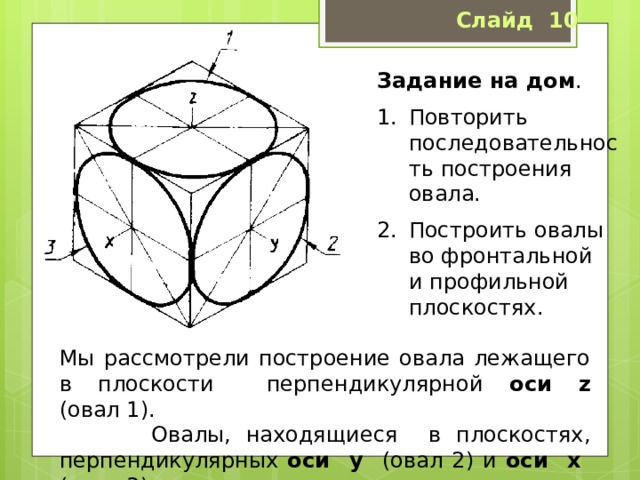
• Повторить последовательность построения овала.
• Построить овалы во фронтальной и профильной плоскостях.

Мы рассмотрели построение овала лежащего в плоскости перпендикулярной оси z (овал 1).

Овалы, находящиеся в плоскостях, перпендикулярных оси y (овал 2) и оси x (овал 3), строят также.

Видео:Аксонометрические проекции (Построение куба и овала)Скачать

Презентация на тему: Проекция окружности в аксонометрии

Проекция окружности в аксонометрии

Автор проекта: Косова О.М. учитель черчения СОШ № 1 г. Усинска

Проекция окружности в аксонометрии

Цели урока: Закрепить знания и умения по построению аксонометрических проекций геометрических фигур и плоскогранных предметов; Развивать приемы работы с циркулем и линейкой; Формировать умения в построении аксонометрических проекций окружности; Воспитывать аккуратность и точность при выполнении работы.

Задание: 1. Начертите оси изометрии (оси проходят под углом 30* к линии горизонта)

2.Начертите квадрат в изометрии (сторона квадрата 80 мм) 3. Найдите точки сопряжения дуг (точки пересечения осей и сторон квадрата- а,b,c,d) 4.Найдите центры больших дуг (А,В)

5.Из вершин А и В проводят дуги радиусом R=Ас=Аd=Ва=Вb

6 Соедините точки B и b, В и а, 7. Найдите центры D и С малых дуг

8. Радиусом r =Db=Dc=Ca=Cd проведите дуги. 9. У вас получился овал — замкнутая кривая, очерченная дугами окружностей.

10.Начертите куб в изометрической проекции и впишите в каждый ромб овал

11. Начертите геометрическое тело — цилиндр

Проверь себя. Как называется окружность выполненная в осях изометрии? Как называется геометрическая фигура при вычерчивании квадрата в осях изометрии? Сколько центров надо найти при вычерчивании овала? Чем на чертеже являются точки a, b, с, d?

📹 Видео

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Черчение "Изометрическая проекция куба со вписанными в стороны куба окружностями."Скачать

1 2 4 сопряжение окружностейСкачать

Лекция №2. Аксонометрические проекции. Виды аксонометрии. Стандартные аксонометрические проекции.Скачать

3 Построение окружности в аксонометрии способ первыйСкачать

Черчение. Аксонометрия. ИзометрияСкачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Врезка куба и шара .Скачать

Аксонометрические проекции. ШестиугольникСкачать