Кто доказал теорему равенства треугольников

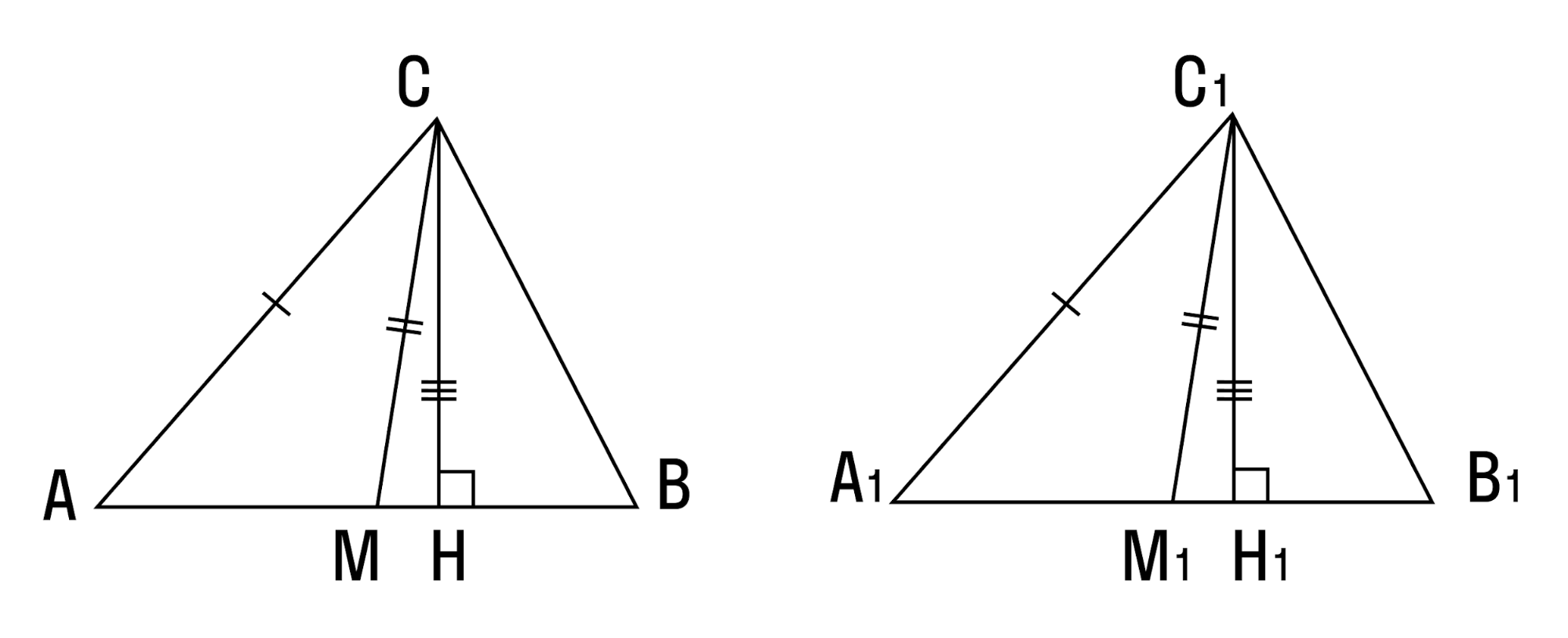
В реферате приводятся доказательств трех признаков равенства треугольников

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Скачать:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ «ИНЖЕНЕРНО-ТЕХНИЧЕСКАЯ ШКОЛА ИМЕНИ ДВАЖДЫ ГЕРОЯ СОВЕТСКОГО СОЮЗА П.Р. ПОПОВИЧА»

«Признаки равенства треугольников»

Выполнила: учащаяся 7 «В» класса Мигунова София

Учитель: Дарья Геннадьевна Исакова

Историческая справка ……………………………………………. 5

Первый признак равенства треугольников ……………………..7

Второй признак равенства треугольников……………………….9

Третий признак равенства треугольников……………………….10

Треугольник является одной из центральных фигур всей геометрии.

При решении задач используют его самые разнообразные свойства.

Свойства треугольника широко применяют на практике: в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности, при проектировании различных деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации для проложения правильного и максимально точного маршрута; в астрологии и астрономии треугольник является очень значимой фигурой; треугольники делают надежными конструкции высоковольтных линий электропередач и железнодорожных мостов.

Кроме того, много других сфер, где применяются различные свойства треугольника: начиная игру в бильярд, необходимо расположить шары в виде треугольника, для этого используют специальное приспособление; расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника; для составления красивых паркетов используются треугольники; устройство треугольника Паскаля: каждое число равно сумме двух расположенных над ним чисел (обвести треугольником три числа). Все элементарно, но сколько в этом таится чудес! Треугольник Паскаля компьютер перевёл на язык цвета.

Тему треугольника можно продолжать неограниченно.

Каких только треугольников нет на свете!

Существуют также переносные значения данной фигуры: например, правило «золотого треугольника» основано на психологии покупателя – найдя нужный ему товар, покупатель устремляется в кассу. Задача продавцов – заставить его задержаться в магазине подольше, расположив нужный покупателю товар в вершинах воображаемого треугольника, то есть «заякорить» покупателя. Чем больше площадь треугольника, тем более удачным можно назвать планировку магазина. В продуктовом магазине этими товарами-якорями являются гастрономия, молочная продукция, хлеб. Задняя торцевая стена торгового зала является вторым местом по значимости и именно там целесообразнее всего располагать товары-якоря – именно для того, что бы заставить покупателя пройти весь периметр магазина.

Широко известный Бермудский треугольник – это район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.

Поэтому изучение треугольника и всех его свойств – очень актуальная тема.

Цель данной работы – рассказать о признаках равенства треугольников, что является одним из важнейших их свойств.

Признаки равенства треугольников — это теоремы, на основании которых можно доказать, что некоторые треугольники равны.

В геометрии используются три признака равенства треугольников.

Данная тема практически изучена, так как на сегодняшний день существуют три признака равенства треугольников, доказываемых с помощью соответствующих теорем.

В глубокой древности вместе с астрономией появилась наука – тригонометрия. Слово «тригонометрия» произведено от греческих «треугольник» и «меряю». Буквальное значение – «наука об измерении треугольников».

С помощью натянутых веревок длиной 3, 4 и 5 единиц египетские жрецы получали прямые углы при возведении храмов и т.п.

Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.

Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию.

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем (рис. 1): пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC и AB ; в противоположном направлении восстанавливают CE и AC так, чтобы точки D (середина AC ), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB . Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).

А вот как в Древнем Египте применили первый признак равенства треугольников ( по двум сторонам и углу между ними), создателем его также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис. 2).

Первый признак равенства треугольников

( по двум сторонам и углу между ними )

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника (рис. 3). Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.

Равенство треугольников ABC и А 1 В 1 С 1 будем обозначать так: Δ ABC = Δ А 1 В 1 С 1 . Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.

Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A 1 B 1 C 1 , (рис. 4) у которых АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 . Докажем, что ΔABC = ΔA 1 B 1 C 1 .

Так как ∠А = ∠А 1 , то треугольник ABC можно наложить на треугольник А 1 В 1 С 1 так, что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и A 1 C 1 . Поскольку АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 а сторона АС — со стороной А 1 C 1 ; в частности, совместятся точки В и В 1 , С и C 1 . Следовательно, совместятся стороны ВС и В 1 С 1 . Итак, треугольники ABC и А 1 В 1 С 1 полностью совместятся, значит, они равны.

Используя этот признак подобия, мы можем измерить высоту любой башни и не только высоту, а спроектировать на чертежах любую постройку.

Для исследования этого признака есть практическая задача на вычисление длины озера (рис. 5).

При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500 м.

Сколько же нужно много свободного пространства чтобы сделать эти измерения? А не легче ли применить второй признак подобия треугольников?

Второй признак равенства треугольников

(по стороне и двум прилежащим к ней углам)

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 6).

При измерении длины озера (рис. 7): так же можно отметить на местности точки А, В и С, а затем еще две точки D и К, так, чтобы отношения DC:CB и KC:AC оказалась равными.

Теорема: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство. Если в △АВС и △А 1 В 1 С 1 будут иметь место следующие равенства AB=А 1 В 1 , ∠BAC=∠B 1 A 1 C 1 , ∠АВС= ∠А 1 В 1 С 1 . Наложим друг на друга треугольники А 1 В 1 С 1 и АВС таким образом, чтобы совпали равные стороны AB и А 1 В 1 и углы, которые к ним прилегают. Как и в уже рассмотренном предыдущем примере, если это необходимо, треугольник А 1 В 1 С 1 можно «перевернуть и приложить обратной стороной». Треугольники совпадут, следовательно, они могут считаться равными.

Третий признак равенства треугольников

(по трем сторонам)

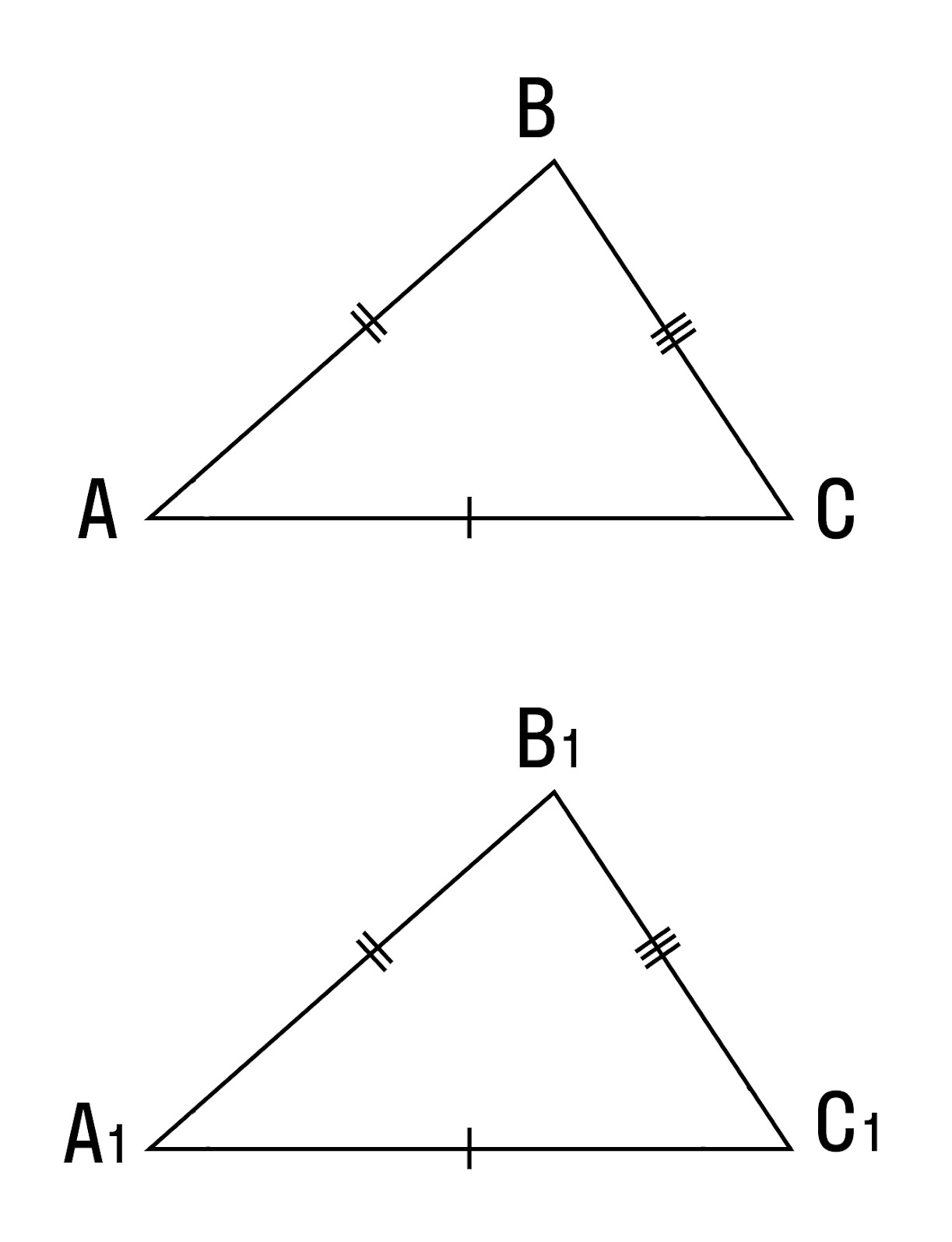
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, (рис. 9) у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой, однако, сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек (рис. 10) Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников (рис. 11).

Если жесткий треугольник мы решим увеличить или уменьшить в несколько раз, то увечится или уменьшится в это число раз каждая его сторона, и тем самым получим третий признак равенства треугольников.

Теорема: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство. Пусть для △ABC и △A 1 B 1 C 1 справедливы равенства А 1 В 1 =АВ, В 1 С 1 =ВС, С 1 А 1 =СА. Переместим треугольник А 1 В 1 С 1 таким образом, что сторона А 1 В 1 совпадет со стороной АВ, и вершины B 1 и B, A 1 и A, совпадут. Возьмем окружность с центром в A и радиусом AC, и вторую окружность с центром B и радиусом BC. Эти окружности пересекутся в двух симметричных относительно отрезка AB точках: точкой C и точкой C 2 . Значит, C1 после переноса треугольника A1B1C1 должна совпасть или с точками C, или с C2. Любом случае, это будет означать равенство △ABC=△A 1 B 1 C 1 , так как треугольники △ABC=△ABC 2 равны (ведь эти треугольники являются симметричными относительно отрезка AB (рис. 12).

Это свойство – жесткость треугольника – широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку; такой же принцип используется при установке кронштейна.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

В данной работе мы изучили такую важную и интересную геометрическую фигуру как треугольник, подробно рассмотрели признаки равенства треугольников, а также их важнейшие свойства и их применение на практике.

Кроме того, обратились к истории возникновения указанных признаков и свойств треугольников, узнали, как в древности проводили различные измерения, провели аналогии с настоящим временем. Ведь в наше время чтобы измерить высоту здания или найти расстояние мы не обходимся без гениальных идей Фалеса Милетского.

Подводя итоги, можно сделать вывод, что главная цель работы достигнута, даны по возможности исчерпывающие ответы на поставленные задачи, освещены все изученные теоремы, отражающие три признака равенства треугольников.

1. Энциклопедия «Аванта» по математике, Москва, 2004 г.

2. «Википедия» — свободная энциклопедия.

3. Глейзер Г.И. «История математики в школе», Москва, Просвещение, 1982 г.

4. Гусева Т.М. Признаки подобия треугольников.- Москва, Первое сентября, приложение «Математика», 1999 г., №28

5. Погорелов А.В. «Геометрия 7-9 классы», Москва, Просвещение, 2003 г.

Видео:Первый признак равенства треугольников | Теорема + доказательствоСкачать

Признаки равенства треугольников

О чем эта статья:

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

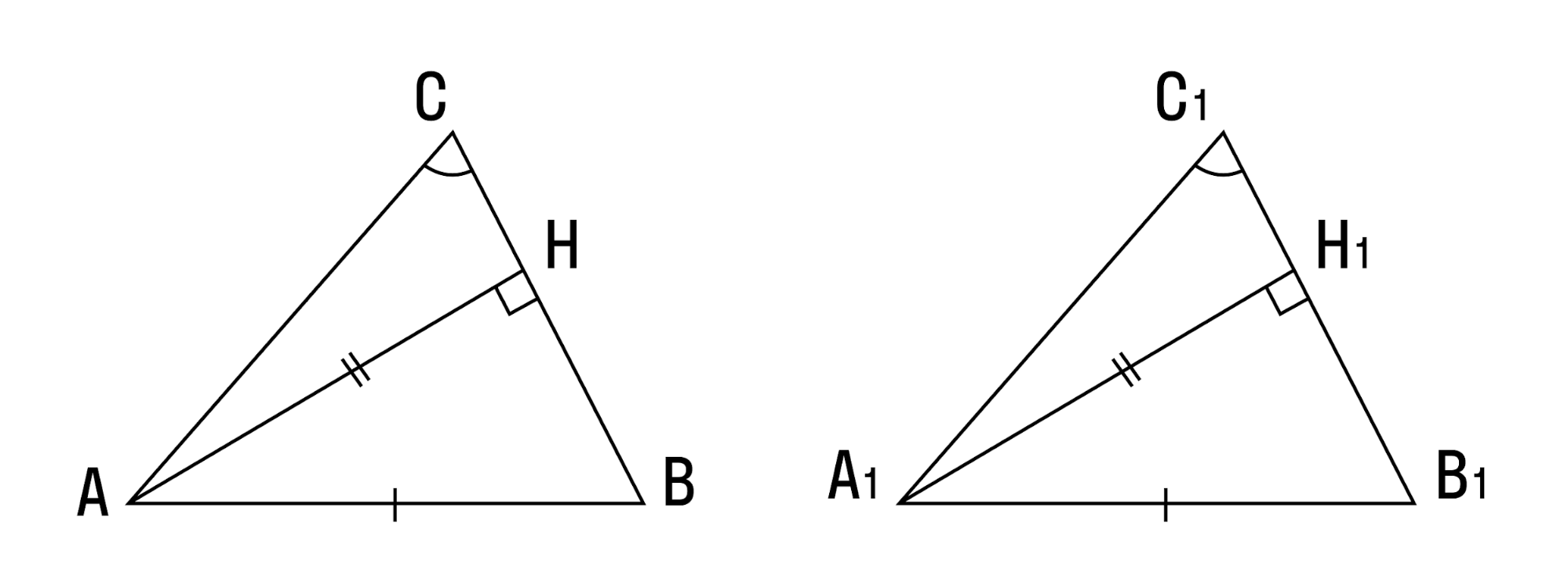
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
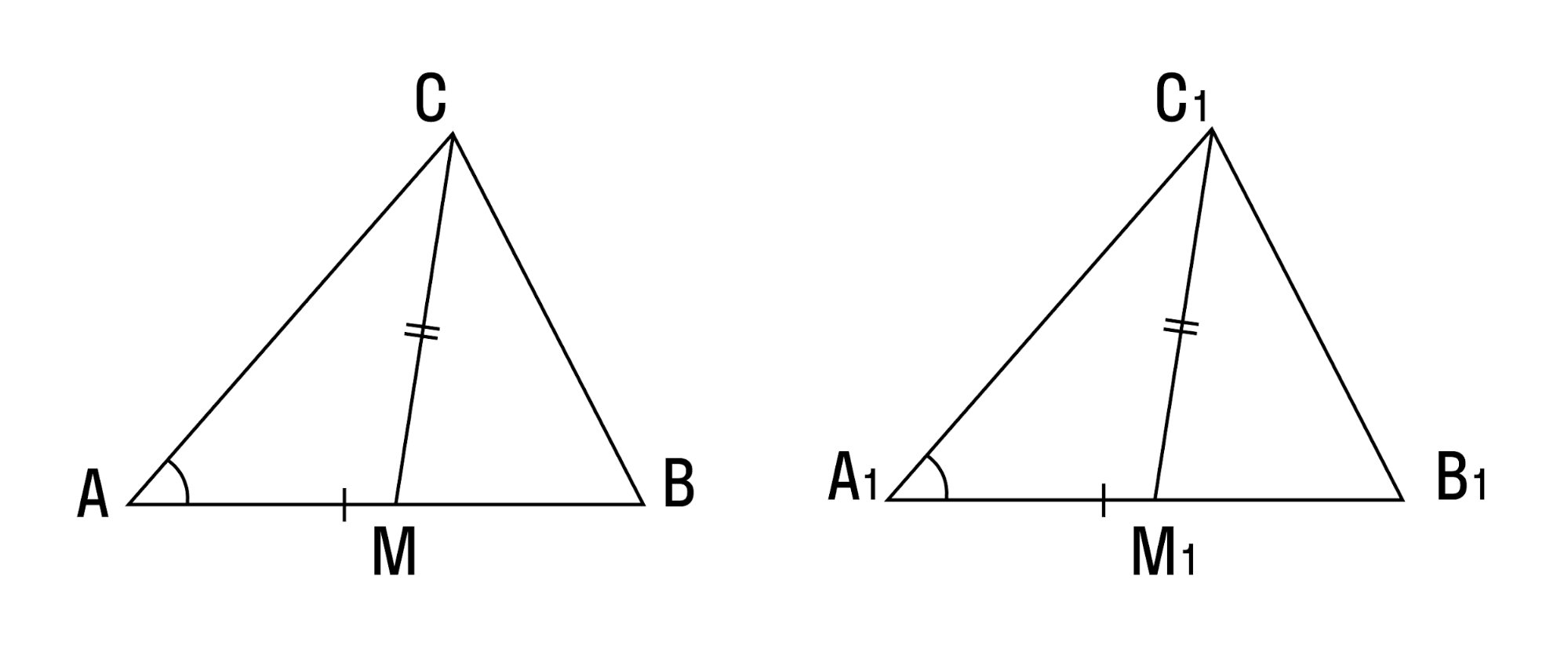
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
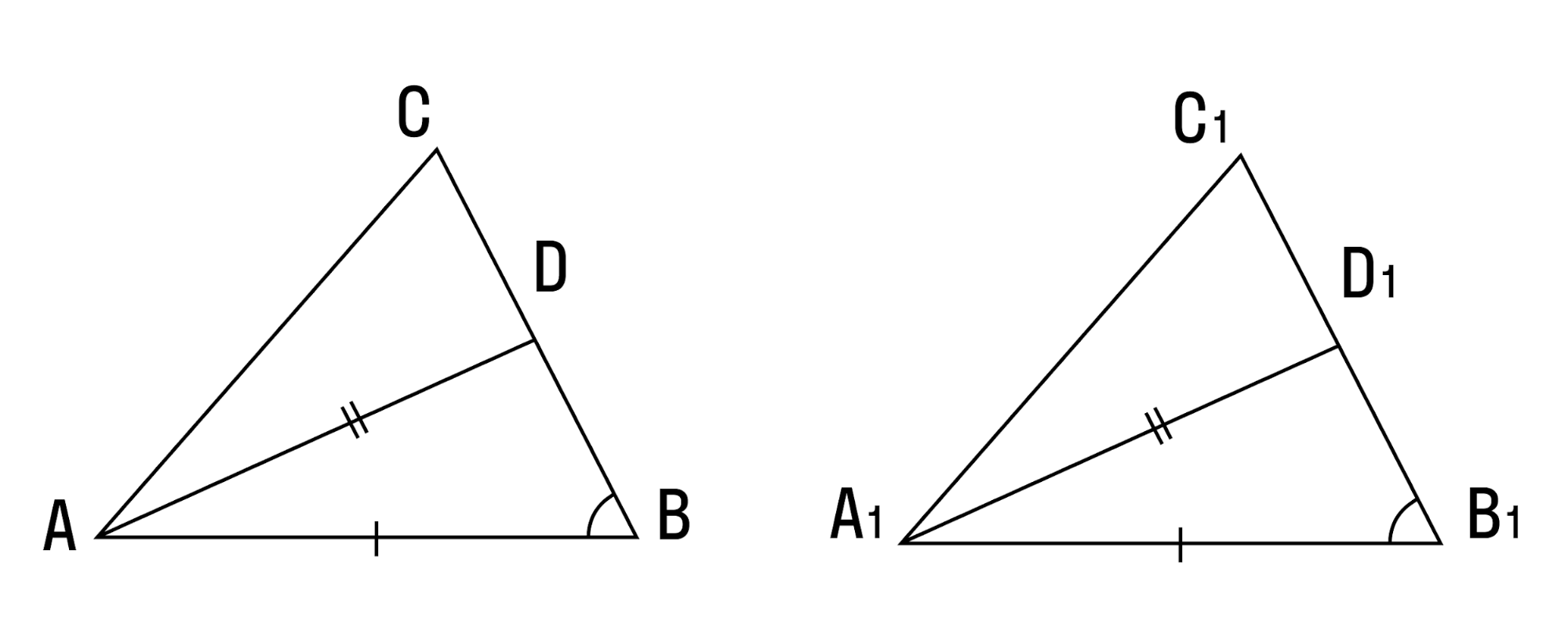
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Второй и третий признаки равенства треугольников

Содержание

Как мы выяснили несколькими уроками ранее, определять равенство между треугольниками можно задействуя меньше данных о фигурах. Нам удалось познакомиться с одним подобным признаком — по равенству двух сторон и углу между ними. Теперь мы готовы разобрать еще два признака равенства, которые пригодятся вам в течение всего курса геометрии.

Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Второй признак равенства треугольников

Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащей к ней углам другого треугольника, то такие треугольники равны.

Пусть имеются треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$, у которых равны стороны $AB$ и $A_B_1$ и углы при этих сторонах — $angle=angle,

angle=angle$. Докажем, что треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны.

Доказательство. Наложим треугольники друг на друга таким образом, что вершина $A$ совпадет с вершиной $A_1$, а вершины $C$ и $C_1$ будут находиться в одной полуплоскости от стороны $AB$. Поскольку $AB=A_B_1$, вершины $B$ и $B_1$ также совпадут при наложении.

Под вопросом остается расположение вершин $C$ и $C_1$ относительно друг друга. Поскольку $angle=angle,$ по аксиоме откладывания угла равного данному лучи $AC$ и $A_C_1$ будут совпадать. Аналогично совпадение лучей $BC$ и $B_C_$ по равенству углов $angle=angle$.

Раз лучи совпадают, точка пересечения лучей — вершина $C$, то вершина $C_1$ находится в той же точке, что и вершина $C$. Все три вершины совпадают, а значит треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны. Теорема доказана .

Запоминать полные формулировки теорем признаков равенства треугольников сложно и может вызвать путаницу. Это придет с опытом решения задач. Пока для вас, возможно, будет удобнее использовать фразу «признак равенства треугольников по…».

Например, второй признак равенства кратко можно перефразировать как «признак равенства треугольников по стороне и прилежащим к ней углам». А как бы вы перефразировали первый?

👍 Все просто: «Признак равенства треугольников по двум сторонам и углу между ними».

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Равнобедренный треугольник: обратная теорема

В точных науках существует понятие обратной теоремы: когда условие исходной теоремы используется в качестве заключения, а заключение — в качестве условия. Чтобы понять, как «работают» обратные теоремы, обратимся для примера к недавно нами доказанной теореме о равнобедренном треугольнике: «В равнобедренном треугольнике углы при основании равны».

— утверждение $A$ — это «равнобедренность треугольника»;
— утверждение $B$ — это «равенство углов при основании».

Логическая операция, к которой мы будем обращаться далее ($Rightarrow$), формально называется импликацией (от лат. ‘implicāre’, в переводе — «впутывать»).

Тогда с точки зрения логики мы можем сказать, что из утверждения $A$ следует утверждение $B$: если $A$, то $B$. Или на языке логики — $ARightarrow$. В обратной теореме утверждения меняются местами — $BRightarrow$, из $B$ следует $A$. В нашем случае читается обратная теорема так: «Если углы при основании равны, то треугольник равнобедренный».

Давайте проверим ее истинность.

Обратная теорема о равнобедренном треугольнике. Если два угла треугольника при основании равны, то такой треугольник является равнобедренным.

Доказательство

Из данного равенства следует, что $AC=BC$. Стороны при основании равны. Тогда $bigtriangleup$ равнобедренный. Теорема доказана.

Об импликациях

Несмотря на то, что прямое и обратное следствия для равнобедренных треугольников оказались истинными, мы не можем, к примеру, сказать то же про вертикальные углы. Действительно, если углы равны… то они вертикальны? Далеко не факт. Иными словами, истинность импликации не гарантирует истинность обратной импликации.

В быту же законы логики соблюдаются редко: мы все время перемешиваем меж собой заключения и условия и, что страшнее, превращаем корреляции в импликации. Например, всем давно известная корреляция между геймингом и детской жестокостью. Нужно понимать, что корреляция — это не более чем статистическая взаимосвязь случайных величин.

Скажем, автомобилист Гриша на третьем перекрестке по дороге домой всегда попадает на зеленый свет светофора. Имеем ли мы право перейти от случайной корреляции к фактическому следствию «если $A$, то $B$»? То есть сказать: «Если Гриша едет домой, то светофор всегда будет зеленым»?

К сожалению, люди размышляют именно так. Корреляция «часто жестокие дети играют в компьютерные игры» превращается в импликацию «если дети играют в игры, то они становятся жестокими».

Или еще хуже, в обратную импликацию: «если ребенок жестокий, то он играет в компьютерные игры».

Первое дает возможность родителям безапелляционно контролировать детей. Второе — снимать какую-либо ответственность за жестокое поведение ребенка с окружения. Импликация — мощное оружие. Особенно когда она используется вне законов науки логики. Так что в следующий раз, если услышите нечто подобное, можете смело заявить о некорректном переходе от корреляции к импликации.

Видео:Геометрия. 7 класс. Теоремы. Т8. Третий признак равенства треугольников.Скачать

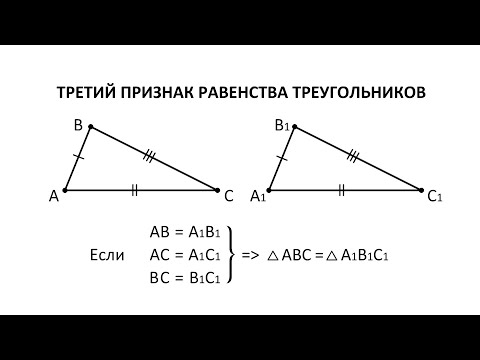
Третий признак равенства треугольников

Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам второго треугольника, то такие треугольники равны.

Доказательство. Даны два треугольника $bigtriangleup$ и $bigtriangleup<A_B_C_1>$, в которых $AB=A_B_1,

BC=B_C_1$ и $CA=C_A_1$. Наложим треугольники друг на друга так, чтобы вершина $C_1$ располагалась в одной полуплоскости с вершиной $C$. Поскольку $AB=A_B_1,$ точка $A$ совпадет с точкой $A_1,$ точка $B$ совпадет с точкой $B_1$.

Воспользуемся методом доказательства от противного и предположим, что при наложении точка $C_1$ не лежит ни на луче $BC$, ни на луче $AC$. Тогда между вершинами $C$ и $C_1$ имеется расстояние $CC_1$. Обозначим точку $D$ как середину этого отрезка.

Рассмотрим треугольники $bigtriangleup<AC_C>$ и $bigtriangleup<BC_C>$.

Они являются равнобедренными, с общим основанием $CC_1$. В них $AD$ и $BD$ — медианы, поскольку $D$ мы обозначали как середину $CC_1$.

По теореме о медиане равнобедренного треугольника, медианы $AD$ и $BD$ также будут являться высотами соответствующих треугольников. Согласно теореме о единственности перпендикуляра, к точке прямой можно провести только один перпендикуляр. У нас — два перпендикуляра $AD$ и $BD$, к одной точке $D$.

Мы пришли к противоречию. Значит, точка $C_1$ располагается либо на луче $AC$, либо на луче $BC$. Если $C_1in,$ тогда $C_1$ совпадает с точкой $C$, поскольку $CA=C_A_1$. Точно так же приходим к выводу о совпадении точек $C$ и $C_1,$ если $C_1in$. Все три точки совпадают. Треугольники равны.

Теорема доказана .

Видео:Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать

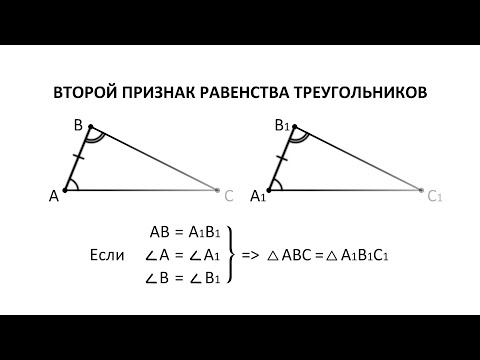
Задача

Попробуйте решить задачу самостоятельно. Ничего страшного, если где-то возникнет заминка: готовое решение находится ниже.

Треугольники $ABC$ и $ABC_1$ равнобедренные, с общим основанием $AB$. Докажите, что треугольники $ACC_1$ и $BCC_1$ равны.

💡 Видео

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Второй признак равенства треугольников. 7 класс.Скачать

7 класс, 20 урок, Третий признак равенства треугольниковСкачать

Геометрия 7. Урок 8 - Признаки равенства треугольников.Скачать

Третий признак равенства треугольников | Теорема + доказательствоСкачать

Второй признак равенства треугольников | Теорема + доказательствоСкачать

7 класс, 19 урок, Второй признак равенства треугольниковСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать