Фронтальные диметрические проекции окружностей

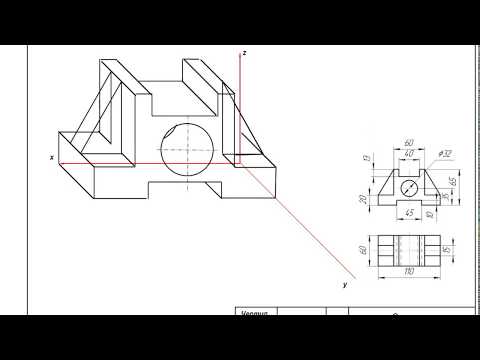
8.1. Фронтальные диметрические проекции окружностей. Если на аксонометрическом изображении хотят некоторые элементы. например окружности (рис. 64), сохранить неискаженными, то применяют фронтальную диметрическую проекцию. Построение фронтальной диметрической проекции детали с цилиндрическим отверстием, два вида которой даны на рисунке 64, а, выполняют так:

1. Пользуясь осями х, у, z, строят тонкими линиями очертания внешней формы детали (рис. 64, б).
2. Находят центр отверстия на передней грани. Через него параллельно оси у проводят ось отверстия и откладывают на ней половину толщины детали. Получают центр отверстия, расположенный на задней грани.
3. Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия (рис. 64, в).
4. Удаляют лишние линии и обводят видимый контур детали (рис. 64, г).

Рис. 64. Построение фронтальной диметрической проекции

Постройте в рабочей тетради фронтальную диметрическую проекцию детали, изображенной на рисунке 64, а. Ось у направьте в другую сторону. Величину изображения увеличьте примерно в два раза.

8.2. Изометрические проекции окружностей. Изометрической проекцией окружности (рис. 65) является кривая, которая называется эллипсом. Эллипсы строить трудно. В практике черчения вместо них часто строят овалы. Овал — замкнутая кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.

Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб

Построение овала, вписанного в ромб, выполняют в такой последовательности.

Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб.

Рис. 66. Построение овала

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б).

Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала.

Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике.

Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x

Рис. 68. Построение изометрической проекции детали с цилиндрическим отверстием

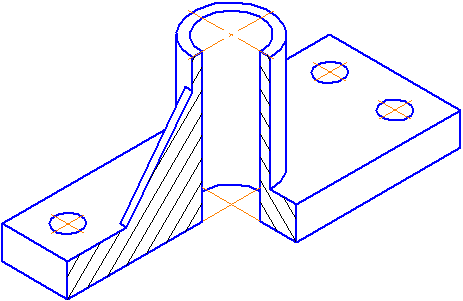
8.3. Способ построения аксонометрических проекций предметов, имеющих круглые поверхности. На рисунке 68, а дана изометрическая проекция планки. Надо изобразить цилиндрическое отверстие, просверленное перпендикулярно передней грани. Построение выполняют так:

1. Находят центр отверстия па передней грани. Определяют направление изометрических осей лля построения ромба (см. рис. 65). Из найденного центра проводят оси (рис. 68, а) и откладывают на них отрезки, равные радиусу окружности.
2. Строят ромб. Проводят его большую диагональ (рис. 68, б).
3. Описывают большие дуги. Находят центры для малых дуг (рис. 68. в).
4. Проводят из найденных центров малые дуги.

Такой же овал строят на задней грани, но обводят лишь видимую его часть (рис. 68, г).

На рисунке 69, а проведены оси для построения трех ромбов. Укажите, на какой грани куба — верхней, боковой правой, боковой левой (см. рис. 65) —будет расположен каждый ромб. Какой оси будет перпендикулярна плоскость каждого из этих ромбов? А какой оси перпендикулярна плоскость каждого из овалов (рис. 69, б)?

Рис. 69. Задание для упражнений

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Аксонометрические проекции

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими .

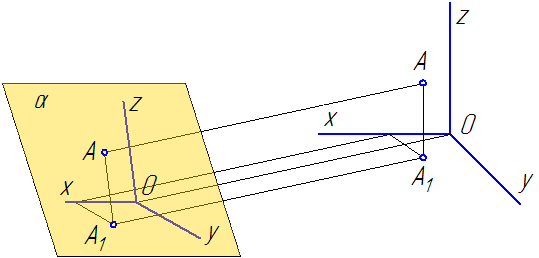
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
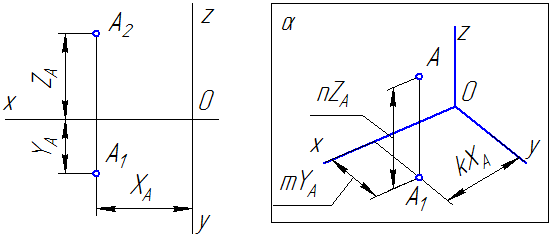
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

• прямоугольные изометрические и диметрические;
• косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

Видео:Прямоугольные диметрические проекцииСкачать

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

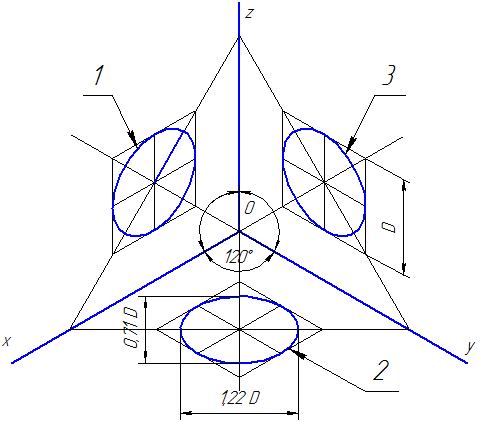
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

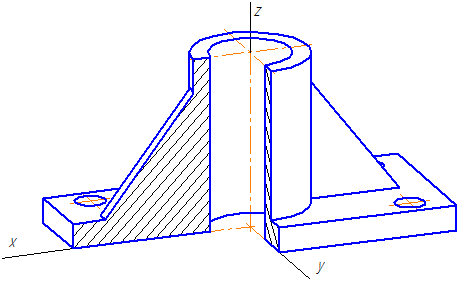
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

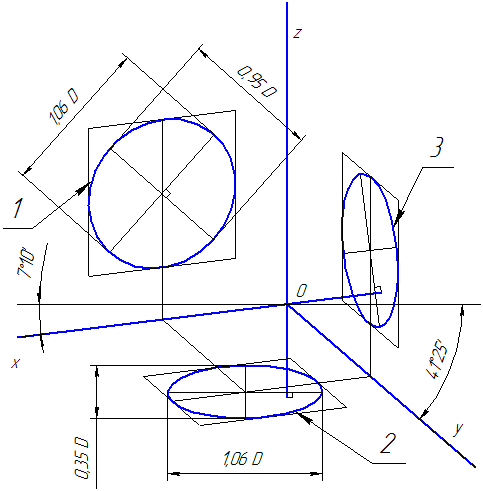
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

Видео:Диметрические проекции.Скачать

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

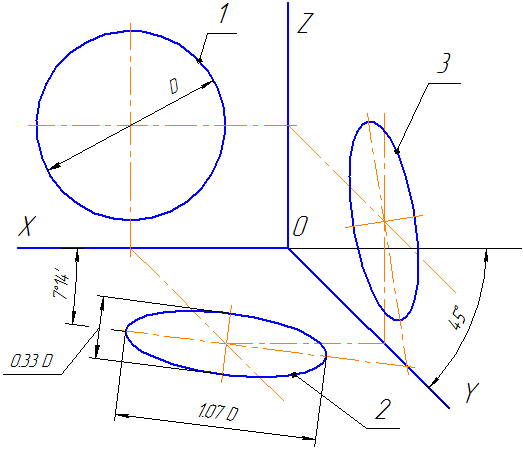
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

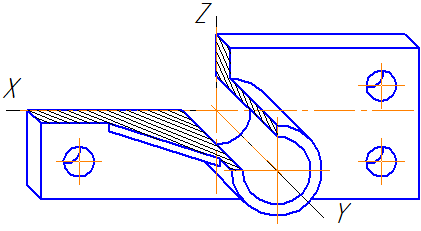
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

Видео:Как начертить овал во фронтальной плоскостиСкачать

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

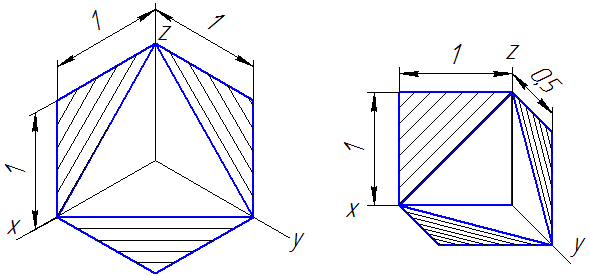
4.4 Штриховка сечений

Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Видео:Косоугольная фронтальная диметрическая проекцияСкачать

Понятие об изображении окружностей во фронтальной диметрической проекции

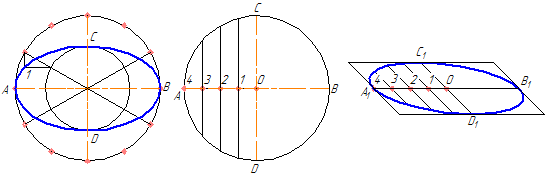
Большинство деталей имеют круглые элементы. Рассмотрим, как во фронтальной диметрической проекции изображаются окружности, плоскости которых соответственно перпендикулярны осям х, у, z.

На рис. 3.10 вычерчено наглядное изображение куба с вписанными в его грани окружностями. Передняя грань куба, параллельная аксонометрической плоскости, проецируется в квадрат, а окружность, вписанная в него, изображается без искажения, т.е. описывается циркулем. Верхняя и боковая стороны куба проецируются в параллелограммы. Поэтому и окружности, вписанные в них, проецируются в эллипсы.

Рис. 3.10. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Изложенное позволяет сделать вывод, что фронтальную проекцию тел вращения целесообразно использовать только в тех случаях, когда деталь можно расположить так, чтобы окружности изображались без искажения и, следовательно, проводились циркулем.

На рис. 3.11 построена фронтальная проекция расположенной подобным образом втулки.

По оси у от точки О отложена высота втулки, сокращенная вдвое (рис. 3.11, а). Из точек О и О1, как из центров, описаны окружности радиусами, равными половине наружного диаметра втулки. К окружностям проведены касательные (они параллельны оси у) (рис. 3.11, б). Из тех же точек О и Οι описаны окружности радиусами, равными половине размера соответствующего отверстия во втулке (рис. 3.11, в). Затем обведен видимый контур (рис. 3.11, г).

Рис. 3.11. Последовательность построения фронтальной диметрической проекции втулки

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Прямоугольная изометрическая проекция

Образование изометрической проекции. Если куб расположить так, чтобы три его грани были наклонены под одинаковым углом к аксонометрической плоскости, и проецировать куб на нее с помощью лучей направленных под прямым углом, то образуется изометрическая проекция (рис. 3.12).

Рис. 3.12. Образование изометрической проекции

«Изометрия» (греч.) – равное измерение. При вычерчивании изометрической проекции размеры по всем трем осям для простоты построения откладывают без сокращения, т.е. натуральные.

Расположение осей х, у, z в изометрической проекции и способ их построения показаны на рис. 3.13. Ось z проводят вертикально, а оси х и у – под углом 30° к горизонтали.

Рис. 3.13. Построение осей изометрической проекции с помощью циркуля

Чтобы построить оси с помощью циркуля и линейки, нужно: из точки О, как из центра, описать дугу любого радиуса; из точки пересечения этой дуги с осью z сделать на дуге тем же раствором циркуля две засечки; точку О соединить прямыми линиями с полученными с помощью засечек точками.

Удобно строить оси и выполнять изометрическую проекцию, пользуясь угольниками с углами 30 и 60°.

Порядок построения изометрических проекций. На рис. 3.14 показано построение изометрической проекции плоской фигуры – правильного шестиугольника (рис. 3.14, а). Для построения вычерчивают изометрические оси х, у, г. Из точки Ο1 по оси х откладывают отрезки O111 и O141 равные размеру отрезков O1 и O4. По этой же оси откладывают отрезки O171 и O181, равные отрезкам O7 и O8. Через полученные точки 71 и 81 проводят параллельно оси у прямые линии. На них откладывают отрезки 71–21, 81–31 и т.д., равные отрезкам 7–2, 8–3 и т.д. Найденные шесть точек последовательно соединяют прямыми (рис. 3.14, б).

Рис. 3.14. Построение изометрической проекции правильного шестиугольника

Построив изометрическую проекцию плоской фигуры, нетрудно вычертить и наглядное изображение призмы, основанием которой она является. Для этого нужно, так же как при построении фронтальной диметрической проекции треугольной призмы (см. рис. 3.6), восставить перпендикуляры из вершин основания (в примере из точек 11, 21, 31, 41, 51, 61) и провести параллельно ребрам нижнего основания ребра верхнего основания.

На рис. 3.15 показаны этапы построения изометрической проекции предмета, чертеж которого приведен на рис. 3.5, а. Вычерчены изометрические оси х, у, z. В плоскости хОу построена передняя грань предмета (рис. 3.15, а). Затем из всех вершин полученной фигуры проведены прямые, параллельные оси у (рис. 3.15, б), так как боковые ребра призмы перпендикулярны передней грани. По оси у отложен отрезок 60 мм и проведены линии, параллельные ребрам передней грани. После этого обведен видимый контур и проставлены размеры (рис. 3.15, в).

Рис. 3.15. Порядок построения изометрической проекции предмета

🔍 Видео

Построение окружности в диметрииСкачать

КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

2 2 3 построение изометрии окружностиСкачать

Изображение в изометрической проекции окружностей, вписанных в кубСкачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Построение эллипса по восьми точкам в прямоугольной диметрииСкачать

Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

Построение прямоугольной изометрии окружностиСкачать

Построение аксонометрии моделиСкачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

Как начертить овал в горизонтальной плоскостиСкачать

ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ КУБА [drawing of a cube dimetric projection]Скачать

Как начертить цилиндр в объемеСкачать

ВМ Диметрия перенос точекСкачать