В треугольнике авс ак

В остроугольном треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.

а) Докажите, что прямые ЕН и АС параллельны;

б) Найдите отношение ЕН : АС, если угол АВС равен 30°.

Заметим, что отрезок AC виден из точек K и M под углом 90°, поэтому точки М, К, С и А лежат на одной окружности, диаметром которой является отрезок АС. Аналогично, точки M, K, H, E лежат на окружности, диаметром которой является MK.

Пусть Тогда так как они опираются на одну дугу KC в окружности, описанной вокруг четырёхугольника AMKC. Кроме того, так как они опираются на одну дугу KH в окружности, описанной вокруг четырёхугольника MKHE. Так как прямые EH и АС параллельны, поскольку это соответственные углы при пересечении EH и AC секущей OA. Это и требовалось доказать.

б) Используем подобие треугольников:

кроме того, поэтому тогда EH =

Тем самым искомое отношение длин сторон равно 3:4.

Приведем другое решение пункта б).

Пусть КС = 2x, тогда из треугольника KHC находим HC = X, из ΔOKC: ∠KOC = 30°, тогда OC = 4x, откуда

В силу подобия ΔOEH и ΔОАС получаем:

Приведем решение Александра Шевкина (Москва).

а) Построим вспомогательную окружность с диаметром MK. Она пройдёт через точки E и H, так как

Построим вспомогательную окружность с диаметром AC. Она пройдёт через точки M и K, т. к.

По свойству вписанных углов а значит, А это соответственные углы при прямых ЕН и АС и секущей AE. Из равенства этих углов следует параллельность прямых ЕН и АС, что и требовалось доказать.

б) Прямая MK, проходящая через основания высот треугольника ABC, отсекает треугольник KMB, подобный треугольнику ABC. Коэффициент подобия равен

Рассмотрим треугольники MOK и EOH. Они подобны по двум углам: (свойство вписанных углов), (вертикальные). Коэффициент подобия равен

Умножив полученные равенства

и

найдём отношение оно равно

Ответ:

Приведем решение Софии Николенко (Москва).

а) Пусть высоты АК и СМ пересекаются в точке О. Рассмотрим треугольник AMO. В нем ME является высотой, проведенной к гипотенузе, поэтому треугольники AME и OME подобны, а углы MAE и OME равны. Пусть эти углы равны α, тогда ∠MOE = 90° − α. Углы KOH и MOE равны 90° − α, тогда угол OKH равен α. Углы EMO и OKH равны так как опираются на одну дугу EH, таким образом, четырехугольник EMKH можно вписать в окружность.

Четырехугольник AMKC также можно вписать в окружность с диаметром AC. Углы KAC и KMC равны, углы KEH и KMC тоже равны, поэтому угол KEH равен углу KAC. Углы KEH и KAC являются соответственными при пересечении прямых EH и AC секущей AO. Таким образом, прямые EH и AC параллельны.

б) Рассмотрим треугольник AMO, пусть ME = x, тогда

Отсюда

Рассмотрим треугольник AME, в нем:

Треугольники AOC и EOH подобны по двум углам. Значит, откуда

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Задание 6

Есть второй способ — в лоб. Находим длины всех сторон и далее по формуле считаем длину медианы. Но этот способ более длинный и не такой красивый, как первый. Воспользуемся первым способом.

AC можно найти довольно легко из прямоугольного треугольника AQC по теореме Пифагора. При этом длины его катетов легко находятся, зная, что медианы делятся точкой пересечения в отношении 2 к 1, считая от вершины. Тогда (AC=sqrt=10.) Тогда третья часть искомой медианы равна 5, а вся медиана, проведенная из вершины B, равна 15.

Видео:Построение медианы в треугольникеСкачать

В треугольнике АВС АС = 22 см, отрезок АК — медиана, АК = 14 см. Найдите стороны АВ и ВС, если АВ: ВС= 7 : 12

Видео:В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

Ваш ответ

Видео:Построение биссектрисы в треугольникеСкачать

решение вопроса

Видео:№545. Треугольники ABC и А1В1С1 подобны, и их сходственные стороны относятся как 6:5Скачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,073
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

💥 Видео

ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Геометрия: В треугольнике АВС известно, что АВ=ВС угол В=32 градуса АК-биссектриса треугольникаСкачать

Построение высоты в треугольникеСкачать

№195. Начертите треугольник ABC и отметьте точку D на стороне АС. Через точку D с помощьюСкачать

Уравнения стороны треугольника и медианыСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

В треугольнике ABC углы А,В и С относятся как 1 :1:7 .Найти углы треугольника ABC.7 кл.ОгэСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

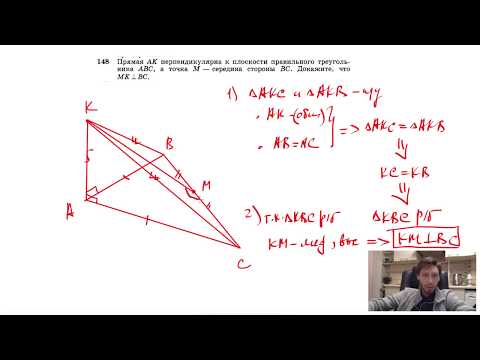
№148. Прямая АК перпендикулярна к плоскости правильного треугольника ABC, М — середина стороны ВС.Скачать

№240. В равнобедренном треугольнике ABC с основанием АС биссектрисы углов А и С пересекаютсяСкачать