Аксиомы стереометрии следствие из аксиомы параллельных прямых (8 видео)

Основные аксиомы стереометрии и следствия из них

Раздел геометрии, в котором изучаются фигуры, расположенные в пространстве, называется стереометрией.

Основными понятиями стереометрии являются точка, прямая и плоскость. Пространство состоит из бесконечного множества точек. Прямые и плоскости состоят из бесконечного множества точек пространства и не совпадают со всем пространством.

Сформулируем основные аксиомы стереометрии. Напомним, аксиомы — это предложения, принимаемые без доказательства. Аксиомы геометрии являются абстракцией соответствующих свойств окружающего нас реального мира.

Будем предполагать, что для любой плоскости пространства выполняются все аксиомы, определения и теоремы планиметрии. Кроме того, будем предполагать справедливыми следующие аксиомы стереометрии:

1. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

2. Если две различные точки прямой принадлежат плоскости, то все точки прямой принадлежат этой плоскости.

3. Если две различные плоскости пересекаются, то они пересекаются по прямой.

Используя эти аксиомы, докажем следующие утверждения:

Следствие 1 . Через прямую и не принадлежащую ей точку проходит единственная плоскость.

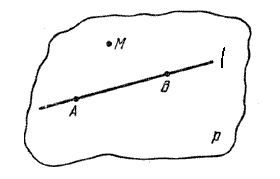
Доказательство. На данной прямой l возьмем какие-нибудь две точки А и В (рис.).

Тогда по аксиоме 1 через данную точку М и точки А и В проходит единственная плоскость р и все точки прямой l принадлежат плоскости р.

Следовательно, плоскость р проходит через прямую l и не принадлежащую ей точку М. Другой такой плоскости нет, так как она должна проходить через три точки А, В, М, не лежащие на одной прямой, и, следовательно, должна совпасть с плоскостью р.

Следствие 2 . Через две пересекающиеся прямые проходит единственная плоскость.

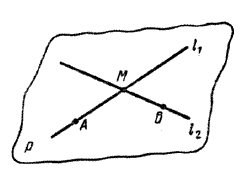
Доказательство. Действительно, пусть прямые 1₁ и 1₂ пересекаются в точке М (рис.).

На прямых 1₁ и 1₂ возьмем какие-нибудь точки A и В, отличные от точки М. Тогда через три точки А, В, М проходит единственная плоскость р. В силу аксиомы 2 плоскость р проходит через данные прямые 1₁ и 1₂.

Содержание

Геометрия. 7 класс
Лекция на тему: «Аксиомы стереометрии. Следствия из них. Взаимное расположение прямых в пространстве.»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
💡 Видео

Видео:Аксиомы стереометрии и их следствия. 10 класс.Скачать

Геометрия. 7 класс

Конспект урока

Аксиома параллельных прямых

Перечень рассматриваемых вопросов:

Аксиомы и теоремы.
Исторические сведения об аксиоматическом построении евклидовой геометрии.
Параллельные и перпендикулярные прямые.
Признаки параллельности прямых.
Решение задач на доказательство параллельности прямых.

Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые, параллельны третьей прямой, то они параллельны.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.

Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.

Аксиома – происходит от греческого «аксиос», что означает «ценный, достойный». Изначально имело смысл «самоочевидная истина».

Теорема – греческое слово, означает «зрелище, представление». В математике греков употреблялось в смысле «истина, доступная созерцанию».

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей прямой, то они параллельны.

Впервые аксиоматический подход к изложению геометрии был изложен в знаменитом сочинении Евклида «Начала» в III веке до нашей эры. Геометрию, которую мы изучаем, по сей день, называют евклидовой. Схема изучения геометрии представлена так: задаются начальные понятия (точка, прямая, плоскость), определения фигур (отрезок, луч, треугольник и др.). Затем изучаются свойства или отношения между ними в виде аксиом или теорем.

Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.

Через любые две точки проходит прямая, и притом только одна.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.

Евклид является автором аксиоматического подхода к построению геометрии.

Аксиома параллельных прямых:

через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

На рисунке через точку М проведены две прямые. Но только одна из них прямая b параллельна прямой а.

Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.

Следствия из аксиомы параллельных прямых.

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Доказательство методом от противного.

Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.

2. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство методом от противного.

Пусть a ║ c, b ║ c.

Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.

Разбор заданий тренировочного модуля

№ 1. Доказать существование прямой, параллельной данной.

Проведём через точку М прямую c ┴ а.
Затем проведём прямую b ┴ c.
Так как прямые a и b перпендикулярны прямой c, то они параллельны.

№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.

Сколько из них пересекает прямую р?

1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.

2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Лекция на тему: «Аксиомы стереометрии. Следствия из них. Взаимное расположение прямых в пространстве.»

Видео:Как решить задачи по стереометрии? / Аксиомы стереометрии и следствия из нихСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Аксиомы стереометрии. Следствия из них. Взаимное расположение прямых в пространстве.

Понятие геометрии как науки, геометрической фигуры, стереометрии.

Основные фигуры в пространстве.

Аксиомы стереометрии и их следствия .

Геометрия – это наука, которая изучает свойства геометрических фигур.

Геометрическая фигура – это любая совокупность точек.

Геометрия подразделяется на планиметрию и на стереометрию , которую мы начинаем изучать.

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Мы начнем изучение стереометрии с основных понятий, основных фигур, аксиом, точно также как это делалось в планиметрии.

Основные фигуры в пространстве: точки, прямые и плоскости.

Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.

Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.

На рисунке плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д.

Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,

Основные свойства точек , прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах :

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются. А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Следствие 1. Через прямую a и не лежащую на ней точку A проходит плоскость, и притом только одна.

рис. 9
Следствие 2. Через две пересекающиеся прямые a и b проходит плоскость, и притом только одна.

Решение задач

Дан тетраэдр АВСD (Рис. 11). Даны следующие точки: точка Е – внутренняя точка ребра АВ , точка Р – внутренняя точка отрезка ЕD , точки М и К , соответственно, на ребрах ВD и DС .

Задача 1

а) В какой плоскости лежит прямая

Ответ: . Прямая РЕ лежит в плоскости АВD , так как в этой плоскости лежат две точки этой прямой. Точка Е лежит в плоскости АВD и точка Р лежит в этой же плоскости. Значит, по второй аксиоме все точки прямой РЕ лежат в плоскости АВD .

б) В какой плоскости лежит прямая

Ответ: . Прямая MK лежит в плоскости DBC , так как в этой плоскости лежат две точки этой прямой. Точка M лежит в плоскости DBC и точка K лежит в плоскости DBC . По второй аксиоме все точки прямой MK лежат в плоскости DBC .

в) В каких плоскостях лежит прямая

Ответ: Прямая BD лежит в плоскости BDА и в плоскости BDС . Значит, прямая BD одновременно лежит в двух плоскостях. Прямая BD есть линия пересечения двух плоскостей. Говорят, что грани АBD, BDС пересекаются по прямой BD . Это можно записать так:

г) В каких гранях лежит прямая ?

Ответ: Прямая АB лежит в грани АВС и в грани АBD . Значит, прямая АВ есть линия пересечения двух этих граней.

д) В каких гранях лежит прямая ?

Ответ: Прямая EC лежит в плоскости АВС и в плоскости ECD, так как точки Е и С лежат одновременно в плоскости АВС и в плоскости ECD. Значит, прямая ЕС есть линия пересечения этих плоскостей.

Задача 2.

а) Найдите точку пересечения прямой DК с плоскостью АВС .

Прямая DК содержит точку С . Плоскость АВС содержит точку С . Значит, прямая DК и плоскость АВС пересекаются в точке С .

б) Найдите точку пересечения прямой СЕ с плоскостью АDВ .

Точка Е принадлежит и прямой СЕ , и плоскости АDВ . Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е .

Задача 3.

а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС .

Точка В и точка D одновременно лежат и в АDВ , и в DВС . Значит, . Все точки прямой DВ являются ответом.

б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС .

Точка В и точка D одновременно лежат и в АDВ , и в DВС . Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости.

в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА .

Точки А , D лежат в плоскости АDВ , а также точки А , D лежат в другой плоскости СDА . Значит, АD – линия их пересечения: .

г) Назовите прямые, по которым пересекаются плоскости РDС и АВС .

Плоскость РDС совпадает с плоскостью ЕDС . Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС . Значит, СЕ – это линия пересечения двух плоскостей. .