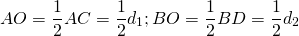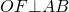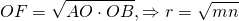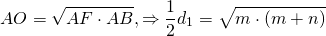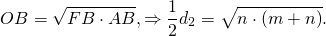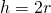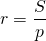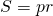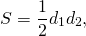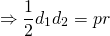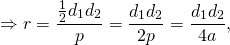Abcd ромб r вписанной окружности 5 fo

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

• d₁ и d₂ – диагонали ромба;
• a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Площадь ромба – формула, пример расчет, как начертить

Через диагонали

Диагональ ромба d₁Диагональ ромба d₂Результат

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Свойства ромба

На рисунке выше ( ABCD ) – ромб, ( AC = DB = CD = AD ) . Так как ромб – это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.

В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:

Формула вычисления площади

1. По длине стороны и высоте:

Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a*h

2. По длине стороны и углу

Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:

S = a 2 *sin α

3. По длинам диагоналей

Площадь ромба равна одной второй произведения его диагоналей.

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Примеры задач

Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.

Решение:
Используем первую формулу, рассмотренную выше: S = 10 см * 8 см = 80 см 2 .

Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.

Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см) 2 * sin 30° = 36 см 2 * 1/2 = 18 см 2 .

Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.

Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 * 4 см * 8 см = 16 см 2 .

Через основание и высоту

Высоты ромба hСторона ромба а

Площади фигур

Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур).Площади фигур

Площадь ромба по углу и противолежащей диагонали

Площадь ромба по углу и диагонали проведенной из этого угла

Способ расчета площади ромба

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – стороны, h – высота

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где d1, d2 – диагонали

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – сторона, α – угол между сторонами

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба:
где r – радиус вписанной окружности, α – угол между сторонами

Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где r – радиус вписанной окружности, a – сторона

Формула площади ромба через две стороны и угол между ними

a — сторона ромба;

— любой угол ромба.

Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.

Решение

По формуле получаем:

S = a 2 ⋅ sin ( α ) = 1 0 0 ⋅ sin ( 3 0 ∘ ) = 5 0 (см. кв.)

Ответ: 50 см. кв.

Формула площади ромба через угол и радиус вписанной окружности

Формула площади ромба через сторону и угол

Таблица с формулами площади ромба

В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	сторона и высота
2	диагонали
3	диагональ и угол между сторонами
4	диагональ и угол между сторонами
5	сторона и угол между сторонами
6	радиус вписанной окружности и угол между сторонами
7	сторона и радиус вписанной окружности

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.

Узнать ещё

Знание — сила. Познавательная информация

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

Точка касания вписанной в ромб окружности делит его сторону на отрезки

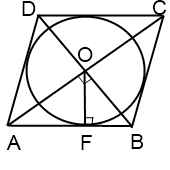
В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

Высота ромба через радиус вписанной окружности

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

Поскольку площадь ромба также равна

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как