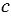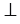Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.
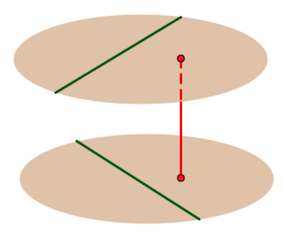
Две плоскости называются параллельными, если они не пересекаются.
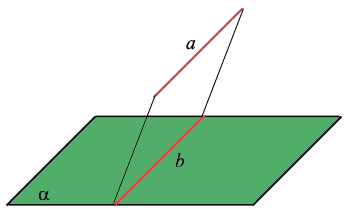
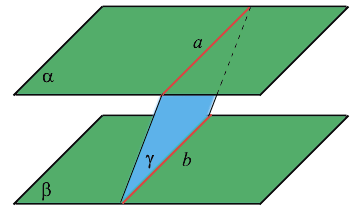
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

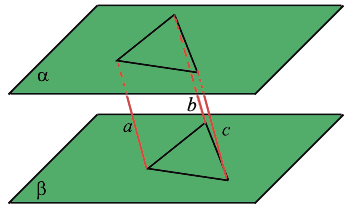
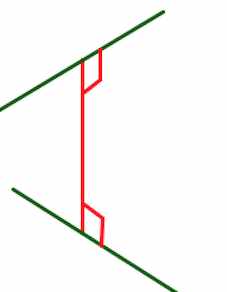
Отрезки параллельных прямых между параллельными плоскостями равны.
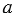

Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.
Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.
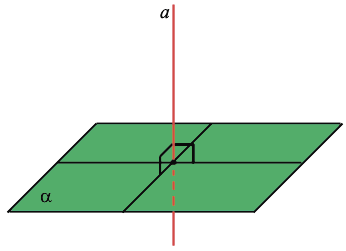
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.
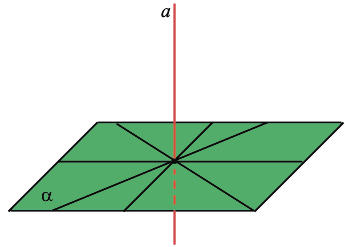
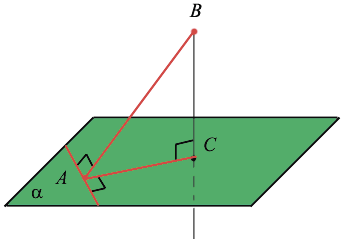
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).
Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
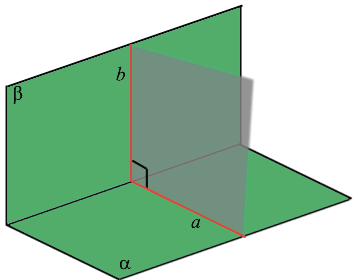
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.
Так как 
Поделись с друзьями в социальных сетях:
Видео:Параллельные, пересекающиеся и скрещивающиеся прямые | МатематикаСкачать

Скрещивающиеся прямые
Скрещивающиеся прямые – прямые, которые невозможно поместить в одну плоскость, то есть они не параллельны и не пересекаются.
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Признак скрещивающихся прямых
Если одна из прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, отличной от точек первой прямой, то такие прямые – скрещивающиеся .
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Расстояние между скрещивающимися прямыми
Через две скрещивающиеся прямые можно провести две параллельные плоскости (единственным образом).
Расстояние между скрещивающимися прямыми – есть расстояние между этими плоскостями.
Видео:Скрещивающиеся прямыеСкачать

Общий перпендикуляр к двум скрещивающимся прямым
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.
Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.
Видео:№94. Даны две скрещивающиеся прямые и точка В, не лежащая на этих прямых. Пересекаются ли плоскостиСкачать

Угол между скрещивающимися прямыми
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
- признаки скрещивающихся прямых;
- определение углов с сонаправленными сторонами;
- доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых;
- доказательство теоремы о равенстве углов с сонаправленными сторонами.
Глоссарий по теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
- Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл.– М.: Просвещение, 2014.
- Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
- Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.
Открытый электронный ресурс:
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)
Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
Одна дорога проходит по эстакаде, а другая под эстакадой
Горизонтальные линии крыши и вертикальные линии стен
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
- Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
|
|
|