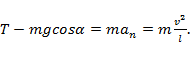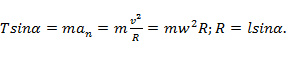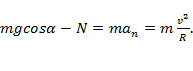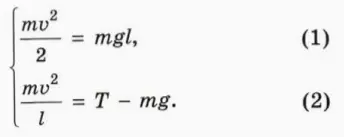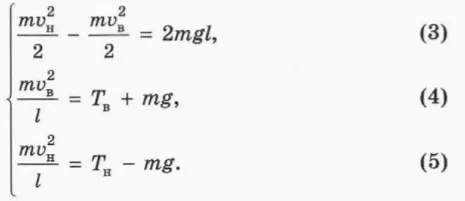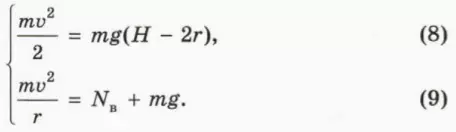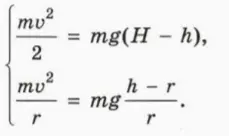Движение тела по окружности подвешенного на нити

Найти линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R=1,5·10 8 км.

Ответ и решение

Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин -1 , посадочная скорость самолета относительно Земли равна 162 км/ч. Определить скорость точки на конце пропеллера. Какова траектория движения этой точки?

Ответ и решение

v ≈ 317 м/с. Точка на конце пропеллера описывает винтовую линию с шагом h ≈ 1,35 м.

Пропеллер самолета вращается с частотой:

λ = 2000/60 с -1 = 33,33 с -1 .

Линейная скорость точки на конце пропеллера:

Скорость самолета при посадке v = 45 м/с.

Результирующая скорость точки на конце пропеллера равна сумме векторов линейной скорости при вращении пропеллера и скорости самолета при посадке:

v_рез = ≈ 317 м/с.

Шаг винтовой траектории равен:

Диск радиусом R катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорость v.

Геометрическим местом точек на диске, имеющих скорость v в данный момент, является дуга радиуса R, центр которой лежит в точке касания диска с плоскостью, т.е. в мгновенном центре вращения.

Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v₁ и v₂.

Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует. Решить задачу для случая, когда скорости реек направлены в разные стороны.

; .

По горизонтальной плоскости катится без скольжения с постоянной скоростью v_c обруч радиусом R. Каковы скорости и ускорения различных точек обруча относительно Земли? Выразить скорость как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча.

v_A = 2v_Ccosα. Ускорение точек обода содержит только центростремительную составляющую, равную a_ц = v 2 /R.

Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение а_цс внешнего слоя резины на покрышках его колес.

На горизонтальную плоскость кладут тонкостенный цилиндр, вращающийся со скоростью v₀ вокруг своей оси. Какой будет скорость движения оси цилиндра, когда прекратится проскальзывание цилиндра относительно плоскости?

Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

Груз массой m может скользить без трения по горизонтальному стержню, вращающемуся вокруг вертикальной оси, проходящей через один из его концов. Груз соединяют с этим концом стержня пружиной, коэффициент упругости которой k. При какой угловой скорости ω пружина растянется на 50% первоначальной длины?

.

Две точечные массы m₁ и m₂ прикреплены к нити и находятся на абсолютно гладком столе. Расстояния от них до закрепленного конца нити равны l₁ и l₂ соответственно.

Система вращается в горизонтальной плоскости вокруг оси, проходящей через закрепленный конец, с угловой скоростью ω. Найти силы натяжения участков нити Т₁ и Т₂.

Человек сидит на краю круглой горизонтальной платформы радиусом R=4 м. С какой частотой n должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения k=0,27?

Тело массой m находится на горизонтальном диске на расстоянии r от оси. Диск начинает раскручиваться с малым ускорением. Построить график зависимости составляющей силы трения в радиальном направлении, действующей на тело, от угловой скорости вращения диска. При каком значении угловой скорости диска начнется соскальзывание тела?

.

Камень массой m=0,5 кг, привязанный к веревке длиной l=50 см, вращается в вертикальной плоскости. Сила натяжения веревки, когда камень проходит низшую точку окружности, Т=44 Н. На какую высоту h над нижней точкой окружности поднимется камень, если веревку перерезать в тот момент, когда его скорость направлена вертикально вверх?

Спортсмен посылает молот (ядро на тросике) на расстояние l=70 м по траектории, обеспечивающей максимальную дальность броска. Какая сила Т действует на руки спортсмена в момент броска? Масса молота m=5 кг. Считать, что спортсмен разгоняет молот, вращая его в вертикальной плоскости по окружности радиусом R=1,5 м. Сопротивление воздуха не учитывать.

Автомобиль массой М=3*10 3 кг движется с постоянной скоростью v=36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R=60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α=10° с вертикалью?

По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2 т. В точке моста, направление на которую из центра кривизны моста составляет с направлением на вершину моста угол α, автомобиль давит с силой F = 14 400 Н. Определить угол α.

Шарик массой m = 100 г подвешен на нити длиной l =1 м. Шарик раскрутили так, что он начал двигаться по окружности в горизонтальной плоскости. При этом угол, составляемый нитью с вертикалью, α = 60°. Определить полную работу, совершаемую при раскручивании шарика.

С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42?

1. Каким должен быть максимальный коэффициент трения скольжения k между шинами автомобиля и асфальтом, чтобы автомобиль мог пройти закругление радиусом R = 200 м при скорости v = 100 км/ч?

2. Автомобиль со всеми ведущими колесами, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности α = 30° радиусом R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю k = 0,3.

Поезд движется по закруглению радиусом R = 800 м со скоростью v = 12 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м.

Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?

1. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м, если коэффициент трения скольжения k = 0,4?

2. На какой угол φ от вертикального направления он должен при этом отклониться?

3. Чему будет равна максимальная скорость мотоциклиста, если он будет ехать по наклонному треку с углом наклона α = 30° при том же радиусе закругления и коэффициенте трения?

4. Каким должен быть угол наклона трека α₀ для того, чтобы скорость мотоциклиста могла быть сколь угодно большой?

Самолет совершает поворот, двигаясь по дуге окружности с постоянной скоростью v = 360 км/ч. Определить радиус R этой окружности, если корпус самолета повернут вокруг направления полета на угол α = 10°.

На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1 м, ширина колеи автомобиля а = 1,5 м. Определить скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит.

Шофер, едущий на автомобиле, внезапно заметил впереди себя забор, перпендикулярный направлению его движения. Что выгоднее сделать, чтобы предотвратить аварию: затормозить или повернуть в сторону?

В вагоне поезда, идущего равномерно по криволинейному пути со скоростью v = 12 км/ч, производится взвешивание груза на пружинных весах. Масса груза m = 5 кг, а радиус закругления пути R = 200 м. Определить показание пружинных весов (силу натяжения пружины Т).

Найти силу F_ед.об., отделяющую сливки (плотность ρ_с = 0,93 г/см 3 ) от снятого молока (ρ_м = 1,03 г/см 3 ) в расчете на единицу объема, если отделение происходит: а) в неподвижном сосуде; б) в центробежном сепараторе, вращающемся с частотой 6000 мин -1 , если жидкость находится на расстоянии r = 10 см от оси вращения.

Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью v = 280 км/ч. С какой силой F тело летчика массой М = 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?

Определить силу натяжения Т каната гигантских шагов, если масса человека М = 70 кг и канат при вращении образует со столбом угол α = 45°. С какой угловой скоростью со будут вращаться гигантские шаги, если длина подвеса l = 5 м?

T ≈ 990 Н; ω ≈ 1,68 рад/с.

Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, α.

.

Грузик, подвешенный на нити, вращается в горизонтальной плоскости так, что расстояние от точки подвеса до плоскости, в которой происходит вращение, равно h. Найти частоту и вращения груза, считая ее неизменной.

. Результат не зависит от длины подвеса.

Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5 м. Определить высоту h, на которую можно отклонить люстру, чтобы при последующих качениях цепь не оборвалась? Известно, что разрыв цепи наступает при силе натяжения Т > 1960 Н.

Шарик массой m подвешен на нерастяжимой нити. На какой минимальный угол α_мин надо отклонить шарик, чтобы при дальнейшем движении нить оборвалась, если максимально возможная сила натяжения нити 1,5 mg?

Маятник отклоняют в горизонтальное положение и отпускают. При каком угле α с вертикалью сила натяжения нити будет равна по величине действующей на маятник силе тяжести? Маятник считать математическим.

Груз массой m, привязанный к нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность сил натяжений нити.

Гимнаст «крутит солнце» на перекладине. Масса гимнаста m. Считая, что вся его масса сосредоточена в центре тяжести, а скорость в верхней точке равна нулю, определить силу, действующую на руки гимнаста в нижней точке.

Один грузик подвешен на нерастяжимой нити длиной l, а другой — на жестком невесомом стержне такой же длины. Какие минимальные скорости нужно сообщить этим грузикам, чтобы они вращались в вертикальной плоскости?

Для нити v_мин = ; для стержня v_мин = .

Шарик массой М подвешен на нити. В натянутом состоянии нить расположили горизонтально и отпустили шарик. Вывести зависимость силы натяжения нити Т от угла α, который образует в данный момент нить с горизонтальным направлением. Проверить выведенную формулу, решив задачу для случая прохождения шарика через положение равновесия, при α = 90°.

Математический маятник длиной l и массой М отвели на угол φ₀ от положения равновесия и сообщили ему начальную скорость v₀, направленную перпендикулярно к нити вверх. Найти силу натяжения нити маятника Т в зависимости от угла φ нити с вертикалью.

.

Грузик, подвешенный на нити, отводят в сторону так, что нить принимает горизонтальное положение, и отпускают. Какой угол с вертикалью α образует пить в тот момент, когда вертикальная составляющая скорости грузика наибольшая?

Одинаковые упругие шарики массой m, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол α и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков?

Математическому маятнику с гибкой нерастяжимой нитью длиной l сообщают из положения равновесия горизонтальную скорость v₀. Определить максимальную высоту его подъема h при движении по окружности, если v₀ 2 = 3gl. По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты подъема h на окружности? Определить максимальную высоту H, достигаемую при этом движении маятника.

; по параболе; .

Маленький шарик подвешен в точке А на нити длиной l. В точке О на расстоянии l/2 ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают. В какой точке траектории исчезает сила натяжения нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик?

На l/6 ниже точки подвеса; по параболе; на 2l/27 ниже точки подвеса.

Сосуд, имеющий форму расширяющегося усеченного конуса с диаметром дна D = 20 см и углом наклона стенок α = 60°, вращается вокруг вертикальной оси 00₁. При какой угловой скорости вращения сосуда ω маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трение не учитывать.

Сфера радиусом R = 2 м равномерно вращается вокруг оси симметрии с частотой 30 мин -1 . Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно сферы, и реакцию сферы N.

Внутри конической поверхности, движущейся с ускорением a, вращается шарик по окружности радиусом R. Определить период Т движения шарика по окружности. Угол при вершине конуса 2α.

.

Небольшое тело массой m соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом R.

Трение ничтожно мало. Определить: а) какова должна быть наименьшая высота h ската, чтобы тело сделало полную петлю, не выпадая; б) какое давление F при этом производит тело на помост в точке, радиус-вектор которой составляет угол α с вертикалью.

Лента конвейера наклонена к горизонту под углом α. Определить минимальную скорость ленты v_мин, при которой частица руды, лежащая на ней, отделяется от поверхности ленты в месте набегания ее на барабан, если радиус барабана равен R.

v_мин = .

Небольшое тело скользит с вершины сферы вниз. На какой высоте h от вершины тело оторвется от поверхности сферы радиусом R? Трением пренебречь.

Найти кинетическую энергию обруча массой m, катящегося со скоростью v. Проскальзывания нет.

Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине h сила нормального давления обруча на стенку ямы равна его силе тяжести? Радиус ямы R, радиус обруча r.

Маленький обруч катится без скольжения по внутренней поверхности большой полусферы. В начальный момент у ее верхнего края обруч покоился. Определить: а) кинетическую энергию обруча в нижней точке полусферы; б) какая доля кинетической энергии приходится на вращательное движение обруча вокруг его оси; в) нормальную силу, прижимающую обод к нижней точке полусферы. Масса обруча равна m, радиус полусферы R.

Вода течет по трубе, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 2 м. Найти боковое давление воды. Диаметр трубы d = 20 см. Через поперечное сечение трубы в течение одного часа протекает М = 300 т воды.

Тело соскальзывает из точки А в точку В по двум искривленным наклонным поверхностям, проходящим через точки A и В один раз по выпуклой дуге, второй — по вогнутой. Обе дуги имеют одинаковую кривизну и коэффициент трения в обоих случаях один и тот же.

В каком случае скорость тела в точке B больше?

В случае движения по выпуклой дуге.

Стержень ничтожной массы длиной l с двумя маленькими шариками m₁ и m₂ (m₁ > m₂) на концах может вращаться около оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость ω и силу давления F на ось в момент прохождения стержнем с шариками положения равновесия.

; .

На виток цилиндрической спирали, ось которой вертикальна, надевают маленькое колечко массой m. Колечко без трения начинает скользить по спирали. С какой силой F будет колечко давить на спираль после того, как оно пройдет n полных витков? Радиус витка R, расстояние между соседними витками h (шаг витка). Считать h ≪ R.

.

Замкнутая металлическая цепочка лежит на гладхом горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском. Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса m = 150 г, длина l = 20 см и цепочка вращается с частотой n = 20 с -1 .

Реактивный самолет m = 30 т летит вдоль экватора с запада на восток со скоростью v = 1800 км/ч. На сколько изменится подъемная сила, действующая на самолет, если он будет лететь с той же скоростью с востока на запад?

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Движение по окружности на нити

Видео:Физика - движение по окружностиСкачать

Движение по окружности (кинематика, динамика)

Найти линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R=1,5·10 8 км.

Ответ и решение

Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин -1 , посадочная скорость самолета относительно Земли равна 162 км/ч. Определить скорость точки на конце пропеллера. Какова траектория движения этой точки?

Ответ и решение

v ≈ 317 м/с. Точка на конце пропеллера описывает винтовую линию с шагом h ≈ 1,35 м.

Пропеллер самолета вращается с частотой:

λ = 2000/60 с -1 = 33,33 с -1 .

Линейная скорость точки на конце пропеллера:

Скорость самолета при посадке v = 45 м/с.

Результирующая скорость точки на конце пропеллера равна сумме векторов линейной скорости при вращении пропеллера и скорости самолета при посадке:

v_рез = ≈ 317 м/с.

Шаг винтовой траектории равен:

Диск радиусом R катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорость v.

Геометрическим местом точек на диске, имеющих скорость v в данный момент, является дуга радиуса R, центр которой лежит в точке касания диска с плоскостью, т.е. в мгновенном центре вращения.

Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v₁ и v₂.

Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует. Решить задачу для случая, когда скорости реек направлены в разные стороны.

; .

По горизонтальной плоскости катится без скольжения с постоянной скоростью v_c обруч радиусом R. Каковы скорости и ускорения различных точек обруча относительно Земли? Выразить скорость как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча.

v_A = 2v_Ccosα. Ускорение точек обода содержит только центростремительную составляющую, равную a_ц = v 2 /R.

Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение а_цс внешнего слоя резины на покрышках его колес.

На горизонтальную плоскость кладут тонкостенный цилиндр, вращающийся со скоростью v₀ вокруг своей оси. Какой будет скорость движения оси цилиндра, когда прекратится проскальзывание цилиндра относительно плоскости?

Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

Груз массой m может скользить без трения по горизонтальному стержню, вращающемуся вокруг вертикальной оси, проходящей через один из его концов. Груз соединяют с этим концом стержня пружиной, коэффициент упругости которой k. При какой угловой скорости ω пружина растянется на 50% первоначальной длины?

.

Две точечные массы m₁ и m₂ прикреплены к нити и находятся на абсолютно гладком столе. Расстояния от них до закрепленного конца нити равны l₁ и l₂ соответственно.

Система вращается в горизонтальной плоскости вокруг оси, проходящей через закрепленный конец, с угловой скоростью ω. Найти силы натяжения участков нити Т₁ и Т₂.

Человек сидит на краю круглой горизонтальной платформы радиусом R=4 м. С какой частотой n должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения k=0,27?

Тело массой m находится на горизонтальном диске на расстоянии r от оси. Диск начинает раскручиваться с малым ускорением. Построить график зависимости составляющей силы трения в радиальном направлении, действующей на тело, от угловой скорости вращения диска. При каком значении угловой скорости диска начнется соскальзывание тела?

.

Камень массой m=0,5 кг, привязанный к веревке длиной l=50 см, вращается в вертикальной плоскости. Сила натяжения веревки, когда камень проходит низшую точку окружности, Т=44 Н. На какую высоту h над нижней точкой окружности поднимется камень, если веревку перерезать в тот момент, когда его скорость направлена вертикально вверх?

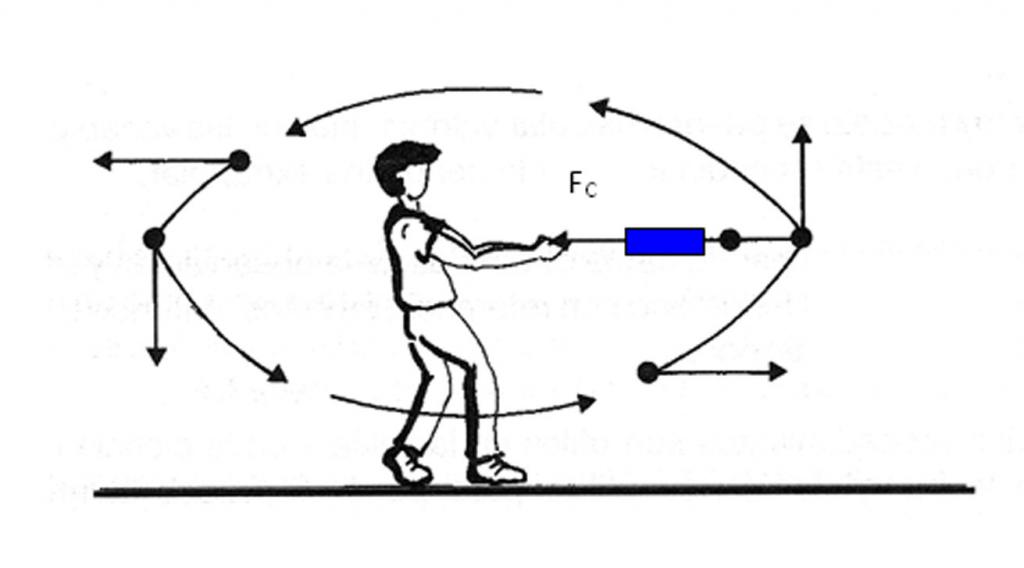
Спортсмен посылает молот (ядро на тросике) на расстояние l=70 м по траектории, обеспечивающей максимальную дальность броска. Какая сила Т действует на руки спортсмена в момент броска? Масса молота m=5 кг. Считать, что спортсмен разгоняет молот, вращая его в вертикальной плоскости по окружности радиусом R=1,5 м. Сопротивление воздуха не учитывать.

Автомобиль массой М=3*10 3 кг движется с постоянной скоростью v=36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R=60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α=10° с вертикалью?

По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2 т. В точке моста, направление на которую из центра кривизны моста составляет с направлением на вершину моста угол α, автомобиль давит с силой F = 14 400 Н. Определить угол α.

Шарик массой m = 100 г подвешен на нити длиной l =1 м. Шарик раскрутили так, что он начал двигаться по окружности в горизонтальной плоскости. При этом угол, составляемый нитью с вертикалью, α = 60°. Определить полную работу, совершаемую при раскручивании шарика.

С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42?

1. Каким должен быть максимальный коэффициент трения скольжения k между шинами автомобиля и асфальтом, чтобы автомобиль мог пройти закругление радиусом R = 200 м при скорости v = 100 км/ч?

2. Автомобиль со всеми ведущими колесами, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности α = 30° радиусом R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю k = 0,3.

Поезд движется по закруглению радиусом R = 800 м со скоростью v = 12 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м.

Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?

1. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м, если коэффициент трения скольжения k = 0,4?

2. На какой угол φ от вертикального направления он должен при этом отклониться?

3. Чему будет равна максимальная скорость мотоциклиста, если он будет ехать по наклонному треку с углом наклона α = 30° при том же радиусе закругления и коэффициенте трения?

4. Каким должен быть угол наклона трека α₀ для того, чтобы скорость мотоциклиста могла быть сколь угодно большой?

Самолет совершает поворот, двигаясь по дуге окружности с постоянной скоростью v = 360 км/ч. Определить радиус R этой окружности, если корпус самолета повернут вокруг направления полета на угол α = 10°.

На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1 м, ширина колеи автомобиля а = 1,5 м. Определить скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит.

Шофер, едущий на автомобиле, внезапно заметил впереди себя забор, перпендикулярный направлению его движения. Что выгоднее сделать, чтобы предотвратить аварию: затормозить или повернуть в сторону?

В вагоне поезда, идущего равномерно по криволинейному пути со скоростью v = 12 км/ч, производится взвешивание груза на пружинных весах. Масса груза m = 5 кг, а радиус закругления пути R = 200 м. Определить показание пружинных весов (силу натяжения пружины Т).

Найти силу F_ед.об., отделяющую сливки (плотность ρ_с = 0,93 г/см 3 ) от снятого молока (ρ_м = 1,03 г/см 3 ) в расчете на единицу объема, если отделение происходит: а) в неподвижном сосуде; б) в центробежном сепараторе, вращающемся с частотой 6000 мин -1 , если жидкость находится на расстоянии r = 10 см от оси вращения.

Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью v = 280 км/ч. С какой силой F тело летчика массой М = 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?

Определить силу натяжения Т каната гигантских шагов, если масса человека М = 70 кг и канат при вращении образует со столбом угол α = 45°. С какой угловой скоростью со будут вращаться гигантские шаги, если длина подвеса l = 5 м?

T ≈ 990 Н; ω ≈ 1,68 рад/с.

Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, α.

.

Грузик, подвешенный на нити, вращается в горизонтальной плоскости так, что расстояние от точки подвеса до плоскости, в которой происходит вращение, равно h. Найти частоту и вращения груза, считая ее неизменной.

. Результат не зависит от длины подвеса.

Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5 м. Определить высоту h, на которую можно отклонить люстру, чтобы при последующих качениях цепь не оборвалась? Известно, что разрыв цепи наступает при силе натяжения Т > 1960 Н.

Шарик массой m подвешен на нерастяжимой нити. На какой минимальный угол α_мин надо отклонить шарик, чтобы при дальнейшем движении нить оборвалась, если максимально возможная сила натяжения нити 1,5 mg?

Маятник отклоняют в горизонтальное положение и отпускают. При каком угле α с вертикалью сила натяжения нити будет равна по величине действующей на маятник силе тяжести? Маятник считать математическим.

Груз массой m, привязанный к нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность сил натяжений нити.

Гимнаст «крутит солнце» на перекладине. Масса гимнаста m. Считая, что вся его масса сосредоточена в центре тяжести, а скорость в верхней точке равна нулю, определить силу, действующую на руки гимнаста в нижней точке.

Один грузик подвешен на нерастяжимой нити длиной l, а другой — на жестком невесомом стержне такой же длины. Какие минимальные скорости нужно сообщить этим грузикам, чтобы они вращались в вертикальной плоскости?

Для нити v_мин = ; для стержня v_мин = .

Шарик массой М подвешен на нити. В натянутом состоянии нить расположили горизонтально и отпустили шарик. Вывести зависимость силы натяжения нити Т от угла α, который образует в данный момент нить с горизонтальным направлением. Проверить выведенную формулу, решив задачу для случая прохождения шарика через положение равновесия, при α = 90°.

Математический маятник длиной l и массой М отвели на угол φ₀ от положения равновесия и сообщили ему начальную скорость v₀, направленную перпендикулярно к нити вверх. Найти силу натяжения нити маятника Т в зависимости от угла φ нити с вертикалью.

.

Грузик, подвешенный на нити, отводят в сторону так, что нить принимает горизонтальное положение, и отпускают. Какой угол с вертикалью α образует пить в тот момент, когда вертикальная составляющая скорости грузика наибольшая?

Одинаковые упругие шарики массой m, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол α и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков?

Математическому маятнику с гибкой нерастяжимой нитью длиной l сообщают из положения равновесия горизонтальную скорость v₀. Определить максимальную высоту его подъема h при движении по окружности, если v₀ 2 = 3gl. По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты подъема h на окружности? Определить максимальную высоту H, достигаемую при этом движении маятника.

; по параболе; .

Маленький шарик подвешен в точке А на нити длиной l. В точке О на расстоянии l/2 ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают. В какой точке траектории исчезает сила натяжения нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик?

На l/6 ниже точки подвеса; по параболе; на 2l/27 ниже точки подвеса.

Сосуд, имеющий форму расширяющегося усеченного конуса с диаметром дна D = 20 см и углом наклона стенок α = 60°, вращается вокруг вертикальной оси 00₁. При какой угловой скорости вращения сосуда ω маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трение не учитывать.

Сфера радиусом R = 2 м равномерно вращается вокруг оси симметрии с частотой 30 мин -1 . Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно сферы, и реакцию сферы N.

Внутри конической поверхности, движущейся с ускорением a, вращается шарик по окружности радиусом R. Определить период Т движения шарика по окружности. Угол при вершине конуса 2α.

.

Небольшое тело массой m соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом R.

Трение ничтожно мало. Определить: а) какова должна быть наименьшая высота h ската, чтобы тело сделало полную петлю, не выпадая; б) какое давление F при этом производит тело на помост в точке, радиус-вектор которой составляет угол α с вертикалью.

Лента конвейера наклонена к горизонту под углом α. Определить минимальную скорость ленты v_мин, при которой частица руды, лежащая на ней, отделяется от поверхности ленты в месте набегания ее на барабан, если радиус барабана равен R.

v_мин = .

Небольшое тело скользит с вершины сферы вниз. На какой высоте h от вершины тело оторвется от поверхности сферы радиусом R? Трением пренебречь.

Найти кинетическую энергию обруча массой m, катящегося со скоростью v. Проскальзывания нет.

Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине h сила нормального давления обруча на стенку ямы равна его силе тяжести? Радиус ямы R, радиус обруча r.

Маленький обруч катится без скольжения по внутренней поверхности большой полусферы. В начальный момент у ее верхнего края обруч покоился. Определить: а) кинетическую энергию обруча в нижней точке полусферы; б) какая доля кинетической энергии приходится на вращательное движение обруча вокруг его оси; в) нормальную силу, прижимающую обод к нижней точке полусферы. Масса обруча равна m, радиус полусферы R.

Вода течет по трубе, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 2 м. Найти боковое давление воды. Диаметр трубы d = 20 см. Через поперечное сечение трубы в течение одного часа протекает М = 300 т воды.

Тело соскальзывает из точки А в точку В по двум искривленным наклонным поверхностям, проходящим через точки A и В один раз по выпуклой дуге, второй — по вогнутой. Обе дуги имеют одинаковую кривизну и коэффициент трения в обоих случаях один и тот же.

В каком случае скорость тела в точке B больше?

В случае движения по выпуклой дуге.

Стержень ничтожной массы длиной l с двумя маленькими шариками m₁ и m₂ (m₁ > m₂) на концах может вращаться около оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость ω и силу давления F на ось в момент прохождения стержнем с шариками положения равновесия.

; .

На виток цилиндрической спирали, ось которой вертикальна, надевают маленькое колечко массой m. Колечко без трения начинает скользить по спирали. С какой силой F будет колечко давить на спираль после того, как оно пройдет n полных витков? Радиус витка R, расстояние между соседними витками h (шаг витка). Считать h ≪ R.

.

Замкнутая металлическая цепочка лежит на гладхом горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском. Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса m = 150 г, длина l = 20 см и цепочка вращается с частотой n = 20 с -1 .

Реактивный самолет m = 30 т летит вдоль экватора с запада на восток со скоростью v = 1800 км/ч. На сколько изменится подъемная сила, действующая на самолет, если он будет лететь с той же скоростью с востока на запад?

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Динамика и кинематика движения по окружности: формулы и решение типовой задачи

Умение описывать движение по окружности является важным для проведения расчетов технических характеристик вращающихся валов и шестерен. Этот вид движения также встречается в быту и природе, например вращение планет вокруг Солнца и фигуристов во время выступления на спортивных соревнованиях. В данной статье рассмотрим, как с точки зрения физики можно описать этот вид движения.

Видео:Центростремительное ускорение. 9 класс.Скачать

Динамика вращения

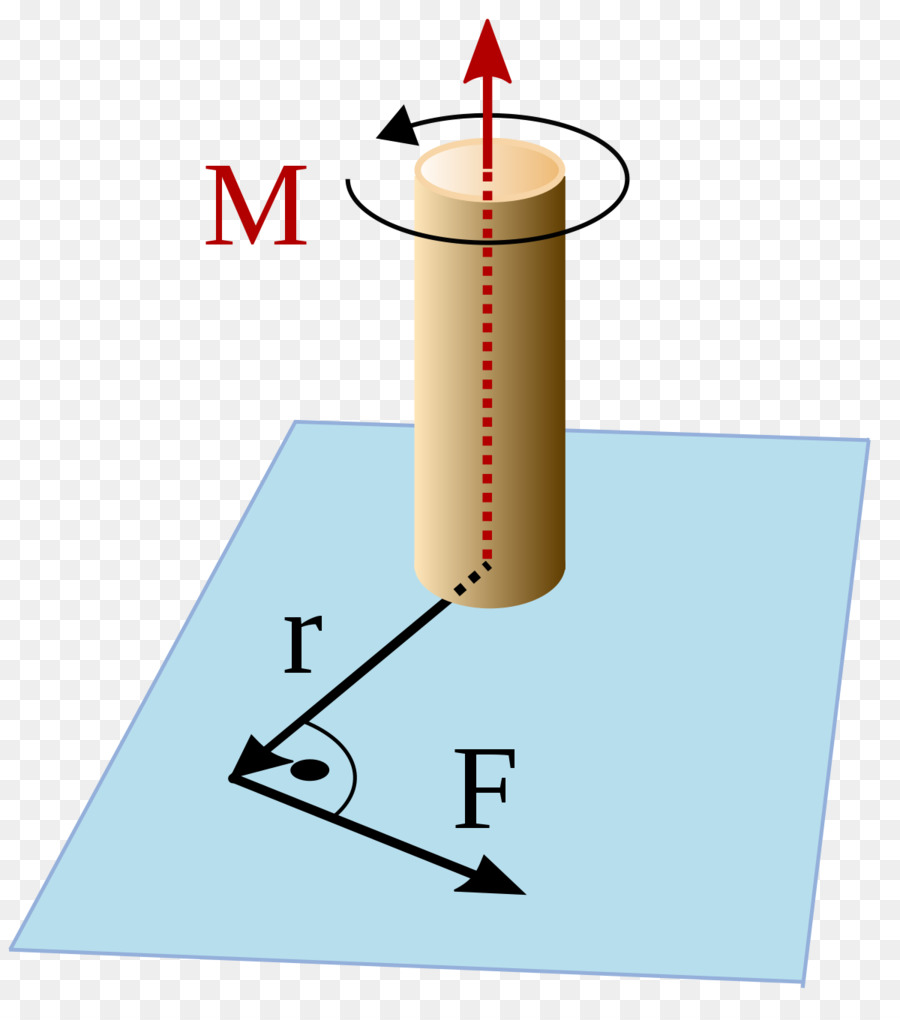
Движение по окружности — это вращение некоторого тела или материальной точки вокруг оси. Чтобы тело начало вращаться, необходимо наличие внешнего момента сил, действующего на рассматриваемую систему. Этот момент определяется по формуле:

Здесь F — сила, d — длина рычага (расстояние между осью и точкой приложения силы). Момент силы является величиной векторной. Приведенная формула используется для расчета модуля M.

Действие момента M отражается на системе в виде появления углового ускорения. То есть система начинает вращаться. Главная формула движения по окружности записывается в виде:

Здесь I — момент инерции, α — ускорение угловое. Обе величины имеют свои аналоги для линейного случая. Если с аналогом величины α все понятно, то для момента инерции I необходимо пояснить. Величина I отражает инерционные свойства вращающейся системы. То есть при вращении она играет такую же роль, как обычная масса тела.

Отметим, что приведенное выражение является аналогом второго закона Ньютона для вращения.

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Центростремительная и центробежная силы, ускорение

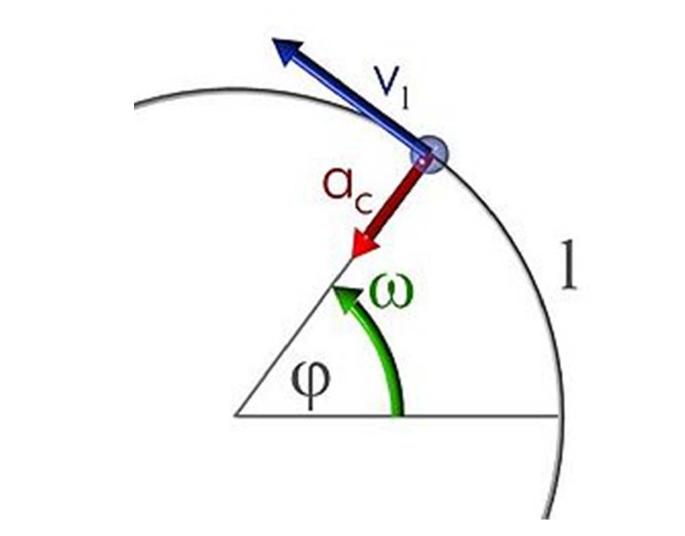
Процесс вращения предполагает наличие некоторой внутренней силы, которая бы обеспечивала криволинейное движение тела. Эта сила называется центростремительной. Согласно названию, она направлена всегда от тела к оси вращения. Поскольку длина рычага d для нее равна нулю, то к возникновению углового ускорения α она не приводит. Тем не менее она изменяет вектор линейной скорости, то есть создает ускорение.

Ускорение при движении по окружности без изменения модуля линейной скорости называется центростремительным. Оно вычисляется по формуле:

Где v — линейная скорость материальной точки, вращающейся на расстоянии r от оси.

Помимо центростремительной, можно часто услышать и о центробежной силе. Последняя стремится вывести тело из круговой траектории на прямолинейную. Причиной ее появления являются инерционные свойства вращающейся системы.

При движении по окружности центростремительная и центробежная силы по модулю равны друг другу, а по направлению они противоположны.

Видео:Движение тел по окружностиСкачать

Кинематические уравнения вращения

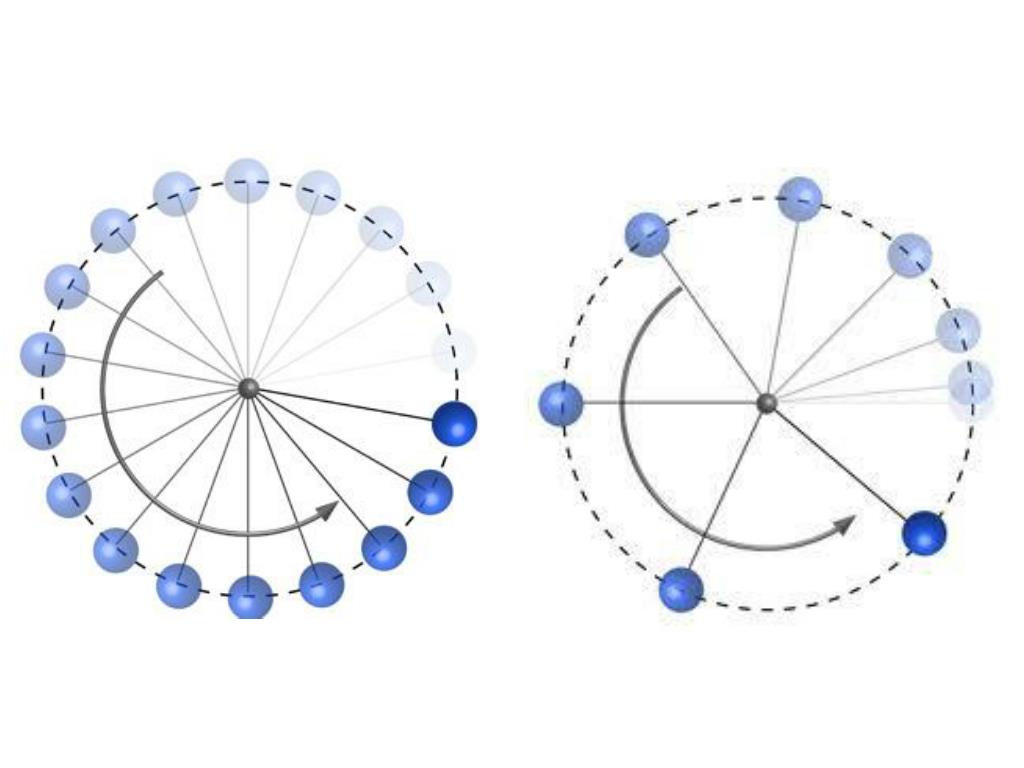
Движение по окружности, как и по прямой линии, может быть равномерным или происходить с ускорением. В первом случае справедлива формула:

То есть центральный угол θ, на который повернется тело за время t, прямо пропорционален угловой скорости ω. Угол θ выражается в радианах, а скорость ω — в радианах в секунду.

Если действует постоянный внешний момент сил на систему, то движение по окружности происходит с некоторым постоянным ускорением α. В таком случае будет справедливо следующее кинематическое выражение:

Если система сначала вращалась с некоторой скоростью ω_0, а затем стала увеличивать частоту своего вращения с ускорением α, то, начиная с момента времени t, когда появилось ускорение, будет справедлива формула:

Заметим, что это выражение является линейной комбинацией двух предыдущих.

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Связь линейных и угловых кинематических характеристик

Выше была приведена формула для центростремительного ускорения, записанная через линейную скорость v. Однако эту формулу можно записать также через соответствующую угловую характеристику ω.

Предположим, что вращающееся тело совершило один оборот по окружности за время t. Тогда для линейной и угловой скоростей можно записать:

Откуда видно, что модуль линейной скорости v в r раз больше модуля величины ω, то есть:

Это равенство связывает угловую и линейную скорости. Используя его, можно записать формулу для a_c через ω:

Теперь вычислим в формуле со скоростями производную по времени для левой и правой частей равенства, получим:

Это равенство связывает направленное по касательной к окружности линейное ускорение a и его угловой аналог α.

Нетрудно доказать, что центральный угол поворота θ при движении по окружности связан с длиной ее дуги L, следующим выражением:

Здесь, если θ будет равен 2*pi радиан (полный оборот), мы получим длину окружности L.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Решение задачи на определение центростремительной силы

Известно, что к веревке длиной 1 метр привязали камень массой 0,5 кг и стали его вращать с угловой частотой 3 об/с. Необходимо найти силу натяжения веревки F_c.

Сила натяжения F_c является центростремительной. Ее можно вычислить по формуле:

Масса камня m известна. Центростремительное ускорение a_c можно рассчитать из знания угловой скорости ω. С заданной в задаче частотой f величина ω связана выражением:

Тогда центростремительное ускорение будет рассчитываться так:

Искомая сила F_c будет равна:

Если из условия задачи подставить данные в эту формулу, то получится значение силы F_c, приблизительно равное 177,5 Н.

Видео:Выполнялка 50. Движение тела по окружностиСкачать

Динамика вращательного движения

При равномерном движении тела по окружности полное ускорение тела определяется только центростремительным ускорением: .

При неравномерном вращении тела по окружности полное ускорение тела равно векторной сумме центростремительного ускорения и касательного (тангенциального) ускорения: .

В задачах ЕГЭ не встречаются вопросы, связанные с нахождением касательного ускорения, однако не стоит забывать о том, что не всякое движение по окружности является равномерным (например, движение маятника, подвешенного на нити), чтобы избежать ошибок при составлении уравнений движения. В таких задачах нужно написать второй закон Ньютона в проекции на радиус вращения (на радиальное направление), тогда проекцией полного ускорения тела будет являться центростремительное ускорение: . Часто в более сложных задачах на динамику вращательного движения необходимо уметь применять закон сохранения энергии (например, для вычисления мгновенной скорости тела).

Типовые задачи

1. Вращение тела в вертикальной плоскости на нити длины l.

Такое движение тела не является равномерным движением по окружности.

Второй закон Ньютона: ;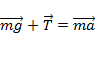

В проекции на ось x (радиальное направление):

Здесь v – мгновенная скорость тела в момент, когда нить составляет с вертикалью угол α.

2. Равномерное вращение тела в горизонтальной плоскости на нити длины l.

Второй закон Ньютона: ;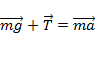

В проекции на ось x (радиальное направление):

В проекции на ось y: . Отметим, что вдоль оси y ускорения нет.

3.Тело без трения скользит по поверхности сферы радиуса R.

Второй закон Ньютона: .

В проекции на ось x (радиальное направление):

4.Тело скользит по внутренней поверхности сферы радиуса R.

Второй закон Ньютона: .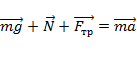

В проекции на ось x (радиальное направление):

В проекции на ось y: =0.

.­­

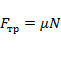
5.Движение спутника по круговой орбите вокруг Земли.

В этом случае сила тяготения Земли сообщает спутнику центростремительное ускорение : .

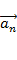
В проекции на ось x: . R – расстояние между центрами Земли и спутника (радиус орбиты спутника).

6.Движение велосипедиста по треку.

При движении велосипедиста по гладкому треку, чтобы двигаться по окружности, велосипедист должен наклониться внутрь траектории, чтобы проекция силы тяжести создала центростремительное ускорение.

Сила реакции опоры проходит через центр тяжести велосипедиста под углом α к треку.

Запишем второй закон Ньютона: .

В проекции на ось x:

В проекции на ось y: ; .

Тангенс угла наклона к треку можно определить по формуле : .

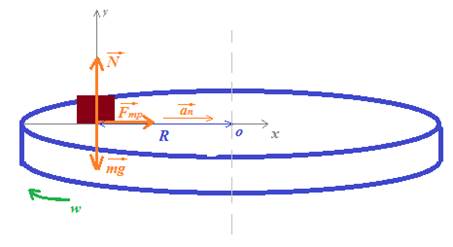
7.Тело вращается вместе с горизонтальной платформой.

Пусть тело массой m лежит на горизонтальной платформе, которая вращается с угловой скоростью w. Коэффициент трения тела о платформу равен µ. Расстояние от тела до оси вращения равно R. Тело будет удерживаться на платформе силой трения . Именно сила трения . создаёт цетростремительное ускорение и совпадает с ним по направлению.

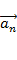
Запишем второй закон Ньютона: .

В проекции на ось x:

В проекции на ось y: ; .

Сила трения:

Статика твёрдого тела.

Основные понятия: момент силы, плечо силы, условие равновесия тел, центр масс, рычаг, золотое правило механики.

Плечо силы — это расстояние от оси вращения до линия действия силы.

AB=h – плечо силы относительно точки O (центр вращения).

Момент силы относительно оси вращения:

.

Момент силы – векторная величина. Направление момента силы определяется по правилу буравчика.

Условия равновесия твёрдого тела:

1)

2)

В задачах ЕГЭ нет необходимости определения направления вектора момента силы, достаточно лишь указать, в какую сторону вращает или вращало бы тело данная сила, и присвоить моменту знак “+” или “-” в зависимости от направления вращения, этот знак следует учесть во втором условии равновесия твёрдого тела.

Центр масс тела – точка тела, которая движется так, как будто на неё действуют только внешние силы, её положение зависит от того, как распределена масса внутри тела.

На рисунке палка, брошенная под углом к горизонту, имеет точку, которая движется как материальная точка только под действием силы тяжести. Эта точка и есть центр масс палки.

Положение центра масс системы тел, определяется по формуле:

Если система состоит из 2 материальных точек массами и , то центр масс такой системы будет расположен где-то на отрезке, соединяющем эти точки, причём ближе к той точке, которая имеет большую массу. В качестве системы координат здесь достаточно выбрать одну ось x, направленную вдоль линии, соединяющей 2 точки. Для упрощения нахождения координаты цетра масс начало координат помещается в одну из материальных точек, что приводит к уменьшению количества слогаемых в формуле.

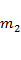
Центр масс твёрдого тела произвольной формы можно найти аналогичным образом, разбив его на элементарные тела, представимые в виде материальных точек.

Рычаг — твёрдое тело, которое может вращаться вокруг неподвижной оси.

Условие равновесия рычага: ; .

Рычаг даёт выигрыш в силе или в расстоянии.

Золотое правило механики: ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Неравномерное движение по окружности в вертикальной плоскости

1. Груз, подвешенный на нити и стержне

Шарик массой m подвешен в точке O на нити длиной l (рис. 33.1). Отведем его на угол 90′ и отпустим без толчка. Шарик начнет двигаться по окружности.

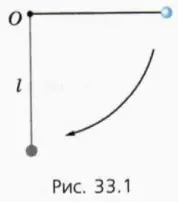
Обозначим скорость, с которой шарик проходит положение равновесия (рис. 33.2).

? 1. Используя рисунок 33.2, ответьте на вопросы:
а) Какие силы показаны на рисунке?
б) Как направлено ускорение шарика?
в) Выразите модуль равнодействующей через модули показанных сил.

? 2. Перенесите в тетрадь рисунок 33.2, укажите на нем ускорение шарика и объясните смысл следующих уравнений:

? 3. Шарик массой 100 г подвешен на нити длиной 1 м. Его отклоняют на 90º и отпускают без толчка.
а) Чему равна сила натяжения нити, когда шарик проходит положение равновесия?
б) Во сколько раз вес шарика при прохождении положения равновесия больше силы тяжести?
Подсказка. Чтобы найти силу натяжения нити, удобно разделить уравнение (2) иа уравнение (1). Вспомните определение веса тела.

Итак, в данном случае при прохождении шариком положения равновесия нить должна выдержать «тройной вес»!

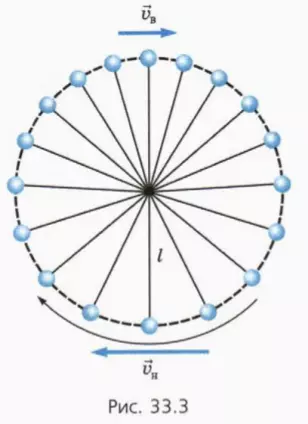
Сообщим шарику в нижней точке такую скорость _н, чтобы он двигался в вертикальной плоскости по окружности (рис. 33.3).

На рисунке показаны последовательные положения шарика через равные промежутки времени (их можно зафиксировать, например, с помощью видеосъемки).

? 4. Почему в верхней части рисунка расстояния между последовательными положениями шарика меньше?

? 5. Сделайте в тетради чертеж, на котором изобразите:
а) силы, действующие на шарик в верхней и нижней точках окружности (обозначьте 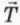_в и _н силы натяжения нити в этих точках);
б) ускорение шарика в этих точках. В верхней точке ускорение направлено вниз, а в нижней – вверх.

? 6. Объясните смысл следующих уравнений:

? 7. Подвешенный на нити шарик массой 100 г вращается в вертикальной плоскости. Насколько больше сила натяжения нити, когда шарик проходит положение равновесия, чем когда он находится в верхней точке окружности?
Подсказка. Удобно вычесть уравнение (4) из уравнения (б) и сравнить полученное уравнение с уравнением (3).

«Шестикратный вес»

Шарик движется но окружности при условии, что нить натянута. Поэтому минимальная скорость, которую нужно сообщить шарику в нижней точке, чтобы он стал двигаться по окружности„должна быть такой, чтобы сила натяжения нити обратилась в нуль только в верхней точке окружности.

? 8. Шарику, подвешенному на нити длиной l, сообщили в нижней точке минимальную горизонтальную скорость, необходимую для того, чтобы он начал двигаться по окружности. Сделайте чертеж, на котором изобразите силы, действующие на шарик в верхней и нижней точках окружности. Чему в этом случае равны:
а) скорость шарика в верхней точке окружности?
б) ускорение шарика в верхней точке окружности?
в) скорость шарика в нижней точке окружности?
г) вес шарика в нижней точке окружности?
Подсказка. Воспользуйтесь уравнениями (3)–(5).

Итак, когда груз проходит нижнюю точку, нить должна выдерживать шестикратный вес груза!

В какой точке шарик сойдет с окружности?

Пусть теперь скорость шарика в нижней точке недостаточна для того, чтобы он мог совершить полный оборот.

В таком случае есть две возможности.

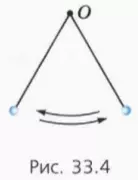
1) Шарик не поднимется выше точки подвеса О. Тогда он начнет колебаться между крайними положениями (рис. 33.4).

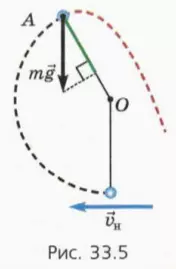
2) Шарик поднимется выше точки подвеса, но сила натяжения нити обратится в некоторой точке А в нуль (рис. 33.5). После этого шарик будет двигаться по параболе, показанной красным пунктиром. Когда шарик находится в точке А, центростремительное ускорение ему сообщает только составляющая силы тяжести, направленная вдоль радиуса к центру окружности. На рисунке показано, как найти модуль этой составляющей (отрезок зеленого цвета).

? 9. Шарику массой m, подвешенному на нити длиной l, сообщают горизонтальную начальную скорость v₀. Когда шарик находится на высоте h, сила натяжения нити обращается в нуль. Обозначим скорость шарика в этот момент. Используя рисунок 33.6:
а) объясните смысл уравнений

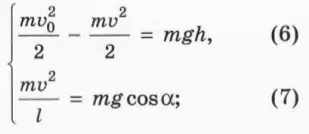
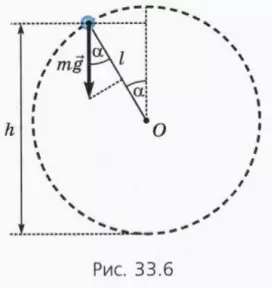
б) выразите h через l и альфа.

? 10. Шарику массой 200 г, подвешенному на нити длиной 50 см, сообщают горизонтальную скорость 4 м/с.
а) До какой высоты (по отношению к положению равновесия) шарик будет двигаться по окружности?
б) Чему будет равна сила натяжения нити, когда шарик будет находиться на одной горизонтали с точкой подвеса?
Подсказка. Когда шарик находится на одной горизонтали с точкой подвеса, центростремительное ускорение шарику сообщает только сила натяжения нити.

? 11. Небольшая шайба массой m лежит внутри закрепленного цилиндра. Ось цилиндра горизонтальна (рис. 33.7). Внутренний радиус цилиндра 30 см, стенки цилиндра гладкие. Какую скорость v0 надо сообщить шайбе перпендикулярно оси цилиндра, чтобы она:
а) совершила полный оборот, двигаясь по окружности?
б) оторвалась от поверхности цилиндра на высоте 40 см?

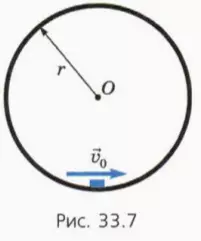
Подсказки. Движение шайбы в цилиндре отличается от движения подвешенного на нити шарика только тем, что роль силы натяжения нити играет сила нормальной реакции, а длину нити l надо заменить на радиус цилиндра r.

Груз, подвешенный на стержне

Рассмотрим теперь вращение груза, подвешенного на легком стержне (массой стержня можно пренебречь). В отличие от нити стержень сохраняет форму и поэтому не дает грузу сойти с окружности. По этой причине минимально возможная скорость груза в верхней точке равна нулю.

? 12. Шарик подвешен на легком стержне длиной l, который может вращаться без трения вокруг точки подвеса O.
а) Какова минимально возможная скорость шарика в верхней точке траектории?
б) Какую минимальную скорость надо сообщить шарику в нижней точке, чтобы он совершил полный оборот?
в) Чему равен вес шарика в нижней точке?

Итак, подвешенному на стержне шарику надо сообщить меньшую начальную скорость, чтобы он сделал полный оборот, чем в случае, когда шарик подвешен на нити той же длины.

2. Движение по «мертвой петле»

Рассмотрим движение тела в вертикальной плоскости по гладкому желобу, переходящему в окружность (рис. 33.8). По аналогии с фигурой высшего пилотажа, когда самолет совершает круговой виток в вертикальной плоскости, такое движение называют иногда мертвой петлей.

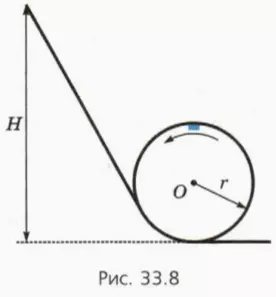
Движение по круговому желобу очень похоже на рассмотренное выше движение подвешенного на нити груза. Роль действующей на груз силы натяжения нити 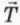играет теперь сила нормальной реакции , направленная тоже по радиусу к центру окружности. А моменту, когда сила натяжения нити обращается в нуль, соответствует момент, когда тело отрывается от желоба.

? 13. Небольшая шайба массой m соскальзывает с высоты H по гладкому наклонному желобу, переходящему в окружность радиусом r, и движется по окружности, не отрываясь от желоба. Обозначим _в силу нормальной реакции, действующую на шайбу в верхней точке окружности. Скорость шайбы в этот момент обозначим v.
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в верхней и нижней точках окружности.
б) Объясните смысл следующих уравнений:

? 14. Чему равна минимальная высота H_min, с которой должна соскальзывать шайба, чтобы она могла совершить полный оборот?
Подсказка. В этом случае N_в обращается в нуль в верхней точке окружности.

Если начальная высота шайбы H меньше, чем Hmin, то в некоторой точке шайба оторвется от желоба. В этой точке сила нормальной реакции обращается в нуль.

? 15. Небольшая шайба массой m соскальзывает с высоты H по гладкому желобу, переходящему в окружность радиусом r, и отрывается от желоба на высоте h (по отношению к нижней точке окружности). Скорость шайбы в этот момент обозначим v.
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от желоба.
б) Используя этот чертеж, объясните смысл уравнений

? 16. Небольшая шайба массой 50 г соскальзывает с некоторой высоты H по гладкому желобу, переходящему в окружность радиусом 30 см, и отрывается от желоба на высоте 40 см (по отношению к нижней точке окружности).
а) Чему равно H?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?

З. Соскальзывание с полусферы

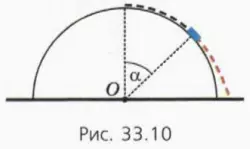
Пусть на вершине гладкой полусферы радиусом г, укрепленной на столе, лежит небольшая шайба массой m (рис. ЗЗ.9). От незначительного толчка шайба начинает соскальзывать.

Пока шайба скользит, действующая на нее сила нормальной реакции уменьшается. В некоторой точке она обратится в нуль – в этот момент шайба оторвется от полусферы (рис. 33.10) и начнет двигаться по параболе (красная пунктирная линия). Обозначим и скорость шайбы в момент отрыва от полусферы.

? 17. Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы, и направление скорости шайбы в этот момент. Обозначьте h высоту, на которой находится при этом шайба, а α – угол между радиусом, проведенный к шайбе и вертикалью. Используя этот чертеж:
а) объясните смысл уравнений

б) выразите h через r и α.
в) выразите h через r.

? 18. На вершине гладкой сферы лежит небольшая шайба массой m, соединенная нитью с грузом массой M (рис. 33.11). В начальный момент тела покоятся. Их отпускают без толчка. Шайба отрывается от полусферы, когда угол между радиусом, проведенным к шайбе, и вертикалью равен α. Обозначим и модуль скорости тел в момент отрыва.

а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы.
Подсказка. В момент отрыва на шайбу действуют только сила тяжести и сила натяжения нити, направленная по касательной к окружности.
б) Насколько опустилась шайба и насколько опустился груз к моменту отрыва шайбы по сравнению с их начальным положением?
Подсказка. См. рисунок 33.12. Шайба опустилась на расстояние, отмеченное синим отрезком, а груз опустился на расстояние (зеленый отрезок), равное длине дуги, пройденной шайбой до отрыва (зеленый пунктир). Длина дуги равна rα (где α задано в радианах).

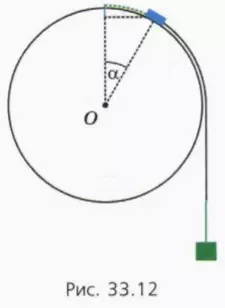
в) Используя этот чертеж, объясните смысл уравнений

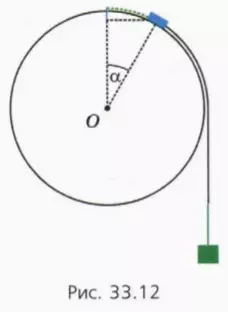
Подсказка. Действующая на шайбу сила натяжения нити направлена по касательной к окружности. Поэтому центростремительное ускорение шайбе перед самым отрывом сообщает только составляющая действующей на шайбу силы тяжести, направленная по радиусу к центру окружности.
г) Чему равно отношение M/m, если α = π/6?

Дополнительные вопросы и задания

19. Какую скорость можно сообщить шарику в нижней точке, чтобы он начал совершать колебания, если:
а) шарик подвешен на нити длиной l?
б) шарик подвешен на легком стрежне длиной l?
Подсказка. Шарик на нити не должен подняться выше точки подвеса, а шарик на стержне не должен достичь верхней точки окружности.

20. Небольшая шайба массой m соскальзывает с высоты H = 2r по гладкому желобу, переходящему в окружность с радиусом r.
а) На какой высоте h (по отношению к нижней точке окружности) шайба оторвется от желоба?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?

21. На гладкой полусфере радиуса r, укрепленной на столе, лежит небольшая шайба. Ей сообщают начальную горизонтальную скорость v0. На какой высоте h от стола шайба оторвется от полусферы?
Подсказка. Если начальная скорость достаточно велика, шайба оторвется от полусферы сразу.

22. На укрепленной на столе полусфере радиуса r лежит небольшая шайба массой m. От незначительного толчка шайба начинает соскальзывать. Вследствие трения за время, в течение которого шайба скользила по полусфере, выделилось количество теплоты Q.
а) На какой высоте h шайба оторвалась от полусферы?
б) На какой высоте h шайба оторвалась от полусферы, если выделившееся количество теплоты равно кинетической энергии шайбы в момент отрыва?

23. Впервые в мире круговой виток в вертикальной плоскости выполнил русский летчик П. Н. Нестеров в 1913 году. Эту фигуру высшего пилотажа называют мертвой петлей или петлей Нестерова. Нестеров так доверял своим расчетам, что перед выполнением мертвой петли не пристегнулся ремнями к креслу пилота. Расчет летчика оказался правильным: ремни не понадобились! Почему при выполнении мертвой петли летчик не выпадает из кресла пилота в верхней точке траектории?

📸 Видео

10 класс - Лабораторная работа № 1 - Изучение движения тела по окружностиСкачать

Лекция 6.1 | Описание движения по окружности | Александр Чирцов | ЛекториумСкачать

Лабораторный эксперимент №4 - Изучение движения тела по окружности (9 класс)Скачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Физика | Равномерное движение по окружностиСкачать

Условие полного оборота шара, подвешенного на нитиСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

9 класс, 24 урок, Движение тел по окружностиСкачать

Физика 9 класс. §18 Движение тела по окружности с постоянной по модулю скоростьюСкачать

Теория. Движение тела по окружности с постоянной по модулю скоростьюСкачать