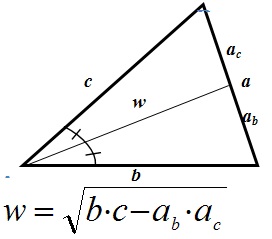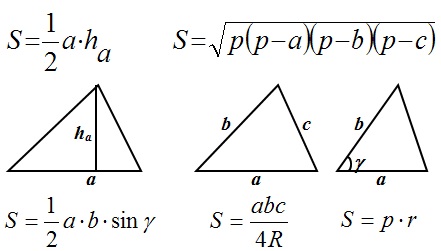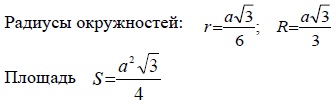16 треугольники четырехугольники многоугольники и их элементы

Видео:Задание №16 ОГЭ. Треугольники, четырёхугольники, многоугольники и их элементы.Скачать

Треугольники, четырёхугольники, многоугольники и их элементы

Перейдем к разбору модуля «Геометрия». В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.

Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.

Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.

В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.

Теория к заданию №16

Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.

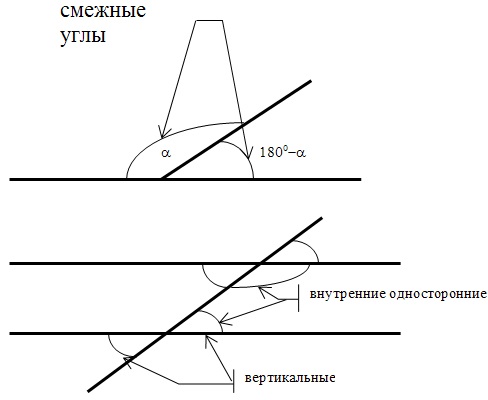
Вначале предлагаю рассмотреть углы на плоскости:

Многие задачи построены на нахождении медиан и биссектрис треугольника:

Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.

• Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
• Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
• Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

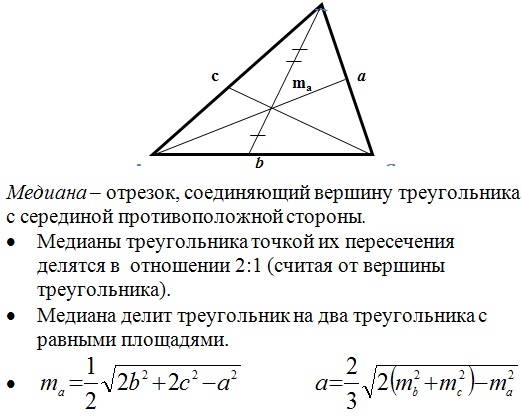
Медиана:

Теперь вспомним основные формулы нахождения площади треугольника:

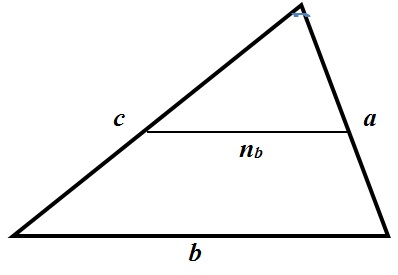
Во многих задачах встречается понятие средняя линия:

Средняя линия – отрезок, соединяющий середины двух сторон треугольника.

• Средняя линия параллельна третьей стороне и равна её половине.
• Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.

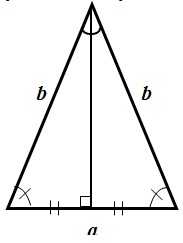
Перейдем к рассмотрению равнобедренного треугольника:

Равнобедренный треугольник — треугольник, у которого две стороны равны.

Свойства равнобедренного треугольника:

• Углы, при основании треугольника, равны.
• Высота, проведенная из вершины, является биссектрисой и медианой.

Рассмотрим равносторонний треугольник:

Равносторонний треугольник — треугольник, у которого все стороны равны.

• Все углы равны 60°.
• Каждая из высот является одновременно биссектрисой и медианой.
• Центры описанной и вписанной окружностей совпадают.

Прямоугольный треугольник:

Разбор типовых вариантов заданий №16 ОГЭ по математике

Первый вариант задания

В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.

Решение:

Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.

Нам известны два угла, значит можем найти третий:

180 — 73 — 48 = 59

Второй вариант задания

Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.

Решение:

Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.

Средняя линия — это линия соединяющая середины сторон и параллельная основанию.

Средняя линия равна половине основания, которому она параллельна.

Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:

MN =½ • AC = 64 / 2 = 32

Третий вариант задания

В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.

Решение:

Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:

Так как углы при основании равны, значит угол BCA равен углу BAC:

58° = ∠BCA + ∠BAC = 2 ∠BCA

Четвертый вариант задания

Сторона равностороннего треугольника равна 10√3. Найдите его медиану.

Решение:

Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:

Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:

m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15

Пятый вариант задания

Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.

Решение:

Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:

Сумма острых углов в прямоугольном треугольнике равна 90°.

Следовательно, второй острый угол равен:

Шестой вариант задания

В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.

Решение:

Для решения необходимо вспомнить определение медианы.

Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.

Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^

AM = ½ AC = ½ 56 = 28

Седьмой вариант задания

Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.

Решение:

Формула площади для прямоугольного треугольника выглядит следующим образом:

Площадь прямоугольного треугольника равна половине произведения его катетов.

Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.

Исходя из вышесказанного, можем решить задачу:

Восьмой вариант задания

Сторона равностороннего треугольника равна 12√3. Найдите его высоту.

Решение:

Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.

Для медианы, а значит и для высоты, формулу я приводил чуть выше:

m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18

Девятый вариант задания

Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.

Решение:

Воспользуемся теоремой Пифагора:

c² = 12² + 16² = 144 + 256 = 400

Десятый вариант задания

Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.

Решение:

До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:

Здесь же нам необходимо решить обратную задачу, найти a, если известно m.

a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22

Демонстрационный вариант ОГЭ 2019

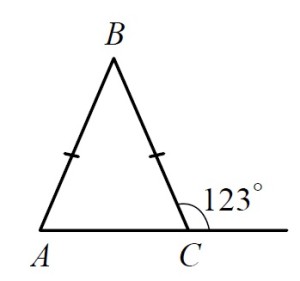
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.

Решение:

Для решения этого задания нужно помнить два факта:

• Внутренний угол с внешним углом дают в сумме 180°
• Углы при основании равнобедренного треугольника равны.

Из первого пункта следует, что угол BCA = 180 — 123 = 57°

Из второго — что ∠BCA = ∠BAC = 57°

Видео:Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать

Задание 16 ОГЭ по Математике. Треугольники, четырёхугольники, многоугольники и их элементы

3. В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180 градусов.

Нам известны два угла. Найдем третий:

180° — 73° — 48° = 59°

4. Сторона равностороннего треугольника равна . Найти его медиану.

Решение.

В равностороннем (правильном) треугольнике медиана m является высотой и биссектрисой. Она находится по формуле:

Здесь a – сторона правильного треугольника. Тогда:

Наш онлайн-курс по Физике

Все темы ЕГЭ с нуля

Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!

Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео

Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

Мы обязательно ответим!

Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.

Результат будет выше, если готовиться по отработанной методике.

У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.

Видео:Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать

Модуль Геометрия

Модуль геометрия первой части содержит пять заданий (16 – 20), каждое из которых оценивается в один балл.

Рекомендую готовить модуль геометрия не по номеру задания, а по темам, в логической последовательности (тригонометрия, углы, треугольники, четырехугольники, окружность), поскольку в задачах 16-19 разные типы фигур встречаются вперемешку. Отдельно нужно готовить задание 20 – анализ геометрических высказываний .

Видео:Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать

Задание №16

Треугольники, четырехугольники, многоугольники и их элементы.
Многоугольники, параллелограмм, ромб, прямоугольник, квадрат, трапеция. Треугольники, прямоугольный треугольник, равнобедренный, равносторонний. Углы.

Видео:Математика ОГЭ. Задание 16. Треугольники, четырехугольники, многоугольники и их элементы. Углы.Скачать

Задание №17

Окружность, круг и их элементы.
Касательная, хорда, секущая, радиус. Окружность, описанная вокруг многоугольника. Центральные и вписанные углы.

Видео:Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать

Задание №18

Площади фигур.
Квадрат, прямоугольник, ромб, параллелограмм, трапеция. Прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, произвольный треугольник.

Видео:Задание 16. Треугольники, четырёхугольники, многоугольники и их элементыСкачать

Задание №19

Фигуры на квадратной решетке.
Площади фигур, расстояние от точки до прямой, векторы.

Видео:Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать

Задание №20

Анализ геометрических высказываний.
Анализ геометрических высказываний , пройденных за 3 года обучения геометрии.

Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Часть 2

Модуль геометрия второй части содержит три задания (24 – 26), каждое из которых оценивается в 2 балла.

Видео:Математика ОГЭ. Задание 16. Треугольники, четырехугольники, многоугольники и их элементы. Углы.Скачать

Задание №24

Геометрическая задача на вычисление.
Окружности, углы, четырехугольники, треугольники.

Видео:ОГЭ по математике 2019. Задание 16. Треугольники, четырёхугольники, многоугольники (часть 1)Скачать

Задание №25

Геометрическая задача на доказательство.
Окружности и их элементы. Треугольники и их элементы. Четырехугольники и их элементы.

Видео:Математика ОГЭ Задание 16. Треугольники, четырехугольники, многоугольники и их элементыСкачать

Задание №26

Геометрическая задача повышенной сложности.
Треугольники, четырехугольники, окружности. Комбинации окружностей и многоугольников.

💥 Видео

16 задание ОГЭ. 11299052. Треугольники, четырёхугольники, многоугольники и их элементыСкачать

Задание 15 ОГЭ 2023 математика | Треугольники, четырёхугольники и их элементыСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задание 15 (часть 5) | ОГЭ 2024 Математика | Четырёхугольники, многоугольники и их элементыСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

16 задание ОГЭ . 16.2.2 . МногоугольникиСкачать